INTRODUCTION
Foot-and-mouth disease (FMD) is a highly infectious disease of cloven-footed animals, responsible for severe epidemics that lead to reduced productivity [Reference Kitching1]. Animals generally recover from the disease but subsequent milk yields and weight are permanently reduced, hence the effects on the livestock industry can be substantial [2]. Although Northern Greece is free from FMD, sporadic epidemics may occur. The specific region is of strategic importance as it represents the southeastern border of Europe and Asia. However, despite the measures taken to prevent the introduction of FMD in the region, northeastern Greece experienced a severe epidemic during 2000. All infected farms detected at the start of the outbreak were in very close proximity to the Evros River, bordering Turkey, and the strain of the virus isolated in Greece during the 2000 epidemic was found to be identical to the strain isolated in Turkey in 1999 and 2000 [3].
Recent modelling approaches for the prediction of FMD occurrence during FMD epidemics include the development of Bayesian spatio-temporal regression models that introduce – in addition to covariate information – Ornstein-Uhlenbeck (OU) stochastic components [Reference Choi4, Reference Branscum5], or discrete-type distributions suitable for this type of data [Reference Choi4, Reference Chhetri, Perez and Thurmond6]. However, to the best of our knowledge, there is an absence of analysis that simultaneously addresses certain characteristics of epidemic data, such as spatio-temporal dependence, environmental noise, multicollinearity issues and the presence of ‘excess’ zeros. An alternative class of models which have been successfully applied to FMD data is based upon suitable extensions of stochastic Susceptible-Infectious-Removed (SIR) models (see e.g. [Reference Jewell7] and references therein). Although the two model classes share certain characteristics since they are, essentially, different versions of a general family of counting processes, there are a number of differences; SIR models focus upon detailed and explicit modelling of the transmission mechanism at the expense of increased computational cost and complex model analysis. On the other hand, our transmission models essentially look at discretized (like daily, weekly or monthly) data and in doing so we (i) gain in computational simplicity, since the model can be fitted in the WinBUGS software [Reference Lunn8], and (ii) by creating the (artificial) extra zeros we are able to see which factors (e.g. environmental) assist in creating a disease-free environment through the covariates linked to the excess zeros.
The epidemiological objective of this work was to assess the impact of various explanatory variables, such as species, environmental factors and the spatial component on the spread of the FMD epidemic in this region. To achieve this we adopted a Bayesian modelling approach that accounts for the frequently observed non-occurrence of the disease in time and space, by implementing zero-inflated distributions [Reference Gan9]. We further incorporate spatial information associated with the locations of infected farms in the form of kernel functions. Multicollinearity issues are also addressed by implementing appropriate Bayesian variable selection techniques. Finally, the incorporation of an OU component into our models allows for structured, autoregressive-type, stochasticity, vital for temporal epidemic data. We show that the utilization of all the above-mentioned modelling strategies has a major impact on model fit and the prediction of disease spread.
Data on the 2000 FMD outbreak
Between July and September, 2000, Greece experienced a major epidemic of FMD. The conducted laboratory tests confirmed the FMD virus, of Asia-1 serotype. In total, about 5600 cattle, 4300 sheep/goats and 360 pigs were culled during the course of the outbreak. No vaccination was used to control the outbreak.
Farm-level data for the 2000 FMD epidemic were provided by the Veterinary Directorate of Northern Evros Prefecture (VDNEP). This dataset has not been previously presented or analysed and presents a unique opportunity to give insight into the true patterns of behaviour of a real epidemic situation of this kind. Figure 1 shows the temporal progress of the disease in terms of disease occurrence.

Fig. 1. Temporal incidence of foot-and-mouth disease outbreaks in 2000 in Evros prefecture, Greece.
Statistical analysis
Model structure
Let y i denote the number of farms with new FMD infections at time t i where i ∈ {0, 1, …, 72} is ordered chronologically first by month and then by day. We assume that
with
and
where g denotes the assumed distribution of the data, λ i is the rate at which new infections take place during the progress/spread of the disease, B t denotes the standard Brownian motion and φ the reversion parameter (i.e. the rate at which the process returns to its long-run mean) of the OU process, which is incorporated into our model through equation (3) for capturing distributional deviations in disease occurrence. Moreover, μ t is a piecewise constant deterministic process given by
 $$\mu _t = \left\{ {\matrix{ {\mu ^{{\rm (0)}}} & {\rm if} & {0 \les t \lt t_{\rm 1}} \cr {\mu ^{{\rm (1)}}} & {\rm if} & {t_1 \les t \lt t_{\rm 2}} \cr \vdots & {} & {} \cr {\mu ^{{\rm (71)}}} & {\rm if} & {t_{71} \les t \lt t_{{\rm 72}}} \cr}} \right.$$
$$\mu _t = \left\{ {\matrix{ {\mu ^{{\rm (0)}}} & {\rm if} & {0 \les t \lt t_{\rm 1}} \cr {\mu ^{{\rm (1)}}} & {\rm if} & {t_1 \les t \lt t_{\rm 2}} \cr \vdots & {} & {} \cr {\mu ^{{\rm (71)}}} & {\rm if} & {t_{71} \les t \lt t_{{\rm 72}}} \cr}} \right.$$with each μ (i) corresponding to t i ⩽ t < t i+1 (i = 0,1,…,71) given by
Here X(i) is the matrix of covariates, and β the vector of the corresponding coefficients, τ is a simple autocorrelation term associated with the influence of the number of FMD cases in the previous day y i−1 on y i. Finally, K(d i, ΘK) is a spatial kernel for the incorporation of spatial information associated with the rate at which infection passes from an infected farm l at times i – j (j = 1, 2, …, 14), i.e. assuming a 2-week incubation period [10], to a susceptible farm k at time i, which captures the fact that FMD is more likely to spread between farms located nearby than farms located farther apart:
 $$\eqalign{& K\left( {d_i,{\bf \Theta }_{\bf K}} \right) = \cr & \left\{ {\matrix{ {\matrix{ {\displaystyle{1 \over {\left\vert {d_i} \right\vert}}\sum\limits_{k \in S_i} {\sum\limits_{l \in I_{i - j}} {K\left( {d_{kl },{\bf \Theta }_{\bf K}} \right)} } } & \matrix{{\hbox{if at least one }} \hfill \cr y_{i - j} \gt 0 \,(\,j = 1,{\rm }2,\ldots,14) \hfill} \cr } } \cr {K\left( {d_{\min },{\bf \Theta }_{\bf K}} \right) \,{\rm if \; all } \,y_{i - j} = 0 \,(\,j = 1,{\rm }2,\ldots,14)} \cr } } \right\}}$$
$$\eqalign{& K\left( {d_i,{\bf \Theta }_{\bf K}} \right) = \cr & \left\{ {\matrix{ {\matrix{ {\displaystyle{1 \over {\left\vert {d_i} \right\vert}}\sum\limits_{k \in S_i} {\sum\limits_{l \in I_{i - j}} {K\left( {d_{kl },{\bf \Theta }_{\bf K}} \right)} } } & \matrix{{\hbox{if at least one }} \hfill \cr y_{i - j} \gt 0 \,(\,j = 1,{\rm }2,\ldots,14) \hfill} \cr } } \cr {K\left( {d_{\min },{\bf \Theta }_{\bf K}} \right) \,{\rm if \; all } \,y_{i - j} = 0 \,(\,j = 1,{\rm }2,\ldots,14)} \cr } } \right\}}$$where |d i| denotes the cardinality of d i, the term K(d kl, ΘK) denotes some specified function of the distance between the infected and susceptible farms based upon their distance d kl and d min, which is set a priori, and restricts the minimum distance over which infections do not occur [Reference Deardon11]. The functional forms that we tested for K are given in Table 1. Selection of the most appropriate forms was based on a variety of relevant functions (e.g. [Reference Chis-Ster and Ferguson12–Reference Szmaragd14]).
Table 1. Summary of spatial kernels K(dkl, ΘK) included in spatio-temporal models

The model specified in equations (1)–(6) can be thought of as an elaborate version of a log-linear type of model for the temporal component, with the addition of an autoregressive term of order 1 (the OU process) and a spatial component captured by K(d kl, ΘK).
Candidate distributions for the epidemic data
For discrete epidemic data, we initially assumed a Poisson P(λ i) or a negative binomial NB(r, q i) distribution. That is
and
respectively.
Importantly, in order to account for the presence of excess zeros, often occurring in epidemic data, we also considered the zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) models. Previous work (e.g. [Reference Malesios15]) has demonstrated that capturing the frequently observed non-occurrence of the disease, by modelling excess zeros in time and space, can considerably improve model fit. To do so, equation (1) takes the following form:
with
Here I {y ij = 0} is an indicator variable for whether or not the FMD cases were observed at time i and p i(0 ⩽ p i ⩽ 1) the probability of observing excess zeros at time i. Finally, the zero-inflated probability p i can be linked to covariates through
with superscript z distinguishing the parameters linking covariates with the probability of excess zeros from those linked to the infection rate in equation (5).
Selection of the best between the Poisson, NB, ZIP and ZINB models is not a trivial matter since the complexity of those models is unclear. In this paper we resort to deviance-based measures due to the well-known equivalence in model selection using cross-validation or Akaike's Information Criterion (see [Reference Stone16]). Given the unknown complexity of the entertained models, we chose to perform model selection based upon the mean deviance ![]() $({\overline D})$ as well as the Deviance Information Criterion, with smaller values for both criteria indicating better fit [Reference Spiegelhalter17].
$({\overline D})$ as well as the Deviance Information Criterion, with smaller values for both criteria indicating better fit [Reference Spiegelhalter17].
Screening selection process of the candidate variables
Candidate variables for inclusion on the final model contained information on several meteorological/environmental predictors as well as size/type of infected farms. The specific variables were chosen based on previous research (see e.g. [Reference Choi4, Reference Keeling13]). (A complete list of all candidate variables along with descriptive statistics can be found in Supplementary Table S1.) The meteorological data were acquired from the Greek National Meteorological Service (http://www.hnms.gr/hnms/english/index_html). Initially we selected the best distributional form and the best kernel function, according to the ![]() ${\overline D}$ values. Then, conditional upon the selection of the best distribution and kernel, we performed a backwards elimination variable selection process, eliminating the least significant variable (at a 5% significance level) each time.
${\overline D}$ values. Then, conditional upon the selection of the best distribution and kernel, we performed a backwards elimination variable selection process, eliminating the least significant variable (at a 5% significance level) each time.
Prior specifications
For the fixed-effects parameters β (accordingly ![]() ${\bi \beta} ^z $) we adopted a g-prior type of approach for specifying the prior distributions in a way that accounts for potential correlations among the explanatory variables. Hence we assumed a multivariate Gaussian prior density, with zero-mean and a prior variance matrix of the form:
${\bi \beta} ^z $) we adopted a g-prior type of approach for specifying the prior distributions in a way that accounts for potential correlations among the explanatory variables. Hence we assumed a multivariate Gaussian prior density, with zero-mean and a prior variance matrix of the form: ![]() $ge^{\beta _{\backslash 0}} ( {{\bf X}_{\backslash 0}^t \cdot {\bf X}_{\backslash 0}} )^{ - 1}$, where
$ge^{\beta _{\backslash 0}} ( {{\bf X}_{\backslash 0}^t \cdot {\bf X}_{\backslash 0}} )^{ - 1}$, where ![]() $\beta _{\backslash 0} $ is the vector β excluding β 0,
$\beta _{\backslash 0} $ is the vector β excluding β 0, ![]() ${\bf X}_{\backslash 0} $ is the data matrix without the intercept, and
${\bf X}_{\backslash 0} $ is the data matrix without the intercept, and ![]() $e^{\beta _{\backslash 0}} $ is a rough estimate of λ i (for more details see [Reference Bové and Held18] or [Reference Malesios19]). Finally, a weakly informative N(0, 104) prior was used for the intercept β 0 and the parameters τ, τ z.
$e^{\beta _{\backslash 0}} $ is a rough estimate of λ i (for more details see [Reference Bové and Held18] or [Reference Malesios19]). Finally, a weakly informative N(0, 104) prior was used for the intercept β 0 and the parameters τ, τ z.
Assessing the impact of different parameters in efficacy of control
An interesting application of the modelling framework adopted in the current study relates to an attempt to measure the relative contribution of the parameters fitted in the final model. The latter is permitted by the decomposition of the covariates included in the final model into two parts: (i) an endemic disease dynamic process, originating outside its internal history, which sums up the effects of significant covariates like those measuring environmental factors and (ii) an epidemic component, which summarizes the effects of significant covariates representing the internal dynamics like farm-to-farm locations and type/size of farms (see [Reference Meyer, Elias and Höhle20]). The latter is achieved via the additive decomposition of μ t, the mean driving the log-rate of infection λ t through:
where μ endemic (μ epidemic) denotes the time-dependent endemic (epidemic) component-related parameters. Within this context, we have an indication of the relative contribution of each part in the spread of the disease. A large epidemic component would suggest imposing restrictions associated with the spatial allocation of farm structure in the region of interest, whereas the opposite results may indicate that most of infections are due to external factors and thus are less sensitive to such control measures.
Posterior predictive model checking
In order to assess the predictive accuracy of our modelling we compared replicated data constructed under the fitted model with the observed data. Hence, simulated values ![]() $y_i^{{\rm rep}} $ are drawn from the posterior predictive distribution of replicated data through
$y_i^{{\rm rep}} $ are drawn from the posterior predictive distribution of replicated data through
and compared to the observed data y i, with similar values between y i and ![]() $y_i^{{\rm rep}} $ indicating a good fit.
$y_i^{{\rm rep}} $ indicating a good fit.
Bayesian inference and convergence diagnostics
We used WinBUGS software to fit the models. The posterior results are obtained after discarding the initial 5000 iterations, using an additional sample of 10 000 iterations (using a thinning lag of 10). Concerning the convergence of the parameters, examination of history plots indicated no lack of convergence for all fitted models. We also examined for autocorrelation through visual inspection of autocorrelation plots for each estimated parameter and found acceptable autocorrelation levels for all parameters. The WinBUGS code for the best selected model with step-by-step explanations is available in the Supplementary material.
RESULTS
From 1 July 2000 until 10 September 2000 a total of 100 farms in the region became infected by FMD. The median number of farms that became infected daily was three (minimum/maximum farms with infections per day was one and 12, respectively, excluding days with zero occurrence). For 42 days during this epidemic no new farms (zero observations) became infected.
Due to the presence of the latter of the models that adjusted for excess zeros, the ZIP model, had the best fit to the data. Under this model, the type A transmission kernel function had the best fit. For all models incorporation of the various spatial kernel functions, which captured the fact that FMD is more likely to spread between farms located nearby, considerably improved model fit. ![]() $\overline D$ values for the four considered distributions and the alternative spatial kernel functions are given in Table 2.
$\overline D$ values for the four considered distributions and the alternative spatial kernel functions are given in Table 2.
Table 2. Mean deviance (![]() ${\overline D}$) for the various fitted models, and mean deviance (
${\overline D}$) for the various fitted models, and mean deviance (![]() ${\overline D}^{\prime}$) for the models that do not include spatial kernels (DIC values in parentheses)
${\overline D}^{\prime}$) for the models that do not include spatial kernels (DIC values in parentheses)

DIC, Deviance Information Criterion; NB, negative binomial; ZIP, zero-inflated Poisson; ZINB, zero-inflated negative binomial.
Under the best model – the ZIP model with the kernel function A – the important predictors were those associated with the epidemic component: the infection rate is only linked to the spatial kernel, whereas the zero part is linked – in addition to the spatial kernel – with the number of cattle and sheep in the farms, finding strong indications that the higher the number of animals within each farm the more likely that it becomes infected. Posterior medians (and the corresponding 95% credible intervals) of the statistically significant estimated coefficients are summarized in Table 3. In addition to the important predictors associated with the model's covariates, we also report parameter φ of the OU process, which is an indicator of the rate at which infections return to the mean infection rate after days with large numbers of cases. The value of 0·035 for the estimated parameter φ of the OU process is low [Reference Yu21] and hence indicative of a slow reduction in the spread of the infection and of the inability of the control measures taken to reduce the infection spread rapidly. This is also expressed by exp ( − φ) = 0·965, that resembles the autocorrelation parameter of an AR(1) process.
Table 3. Posterior medians and corresponding 95% credible intervals of parameters (ZIP model)

OU, Ornstein-Uhlenbeck.
Finally, Figure 2 depicts the temporal endemic/epidemic decomposition of μ t, i.e. the contribution of either the epidemic (μ t_endemic) or endemic (μ t_epidemic) component of the model during the 72 days of the epidemic to the number of newly infected farms.
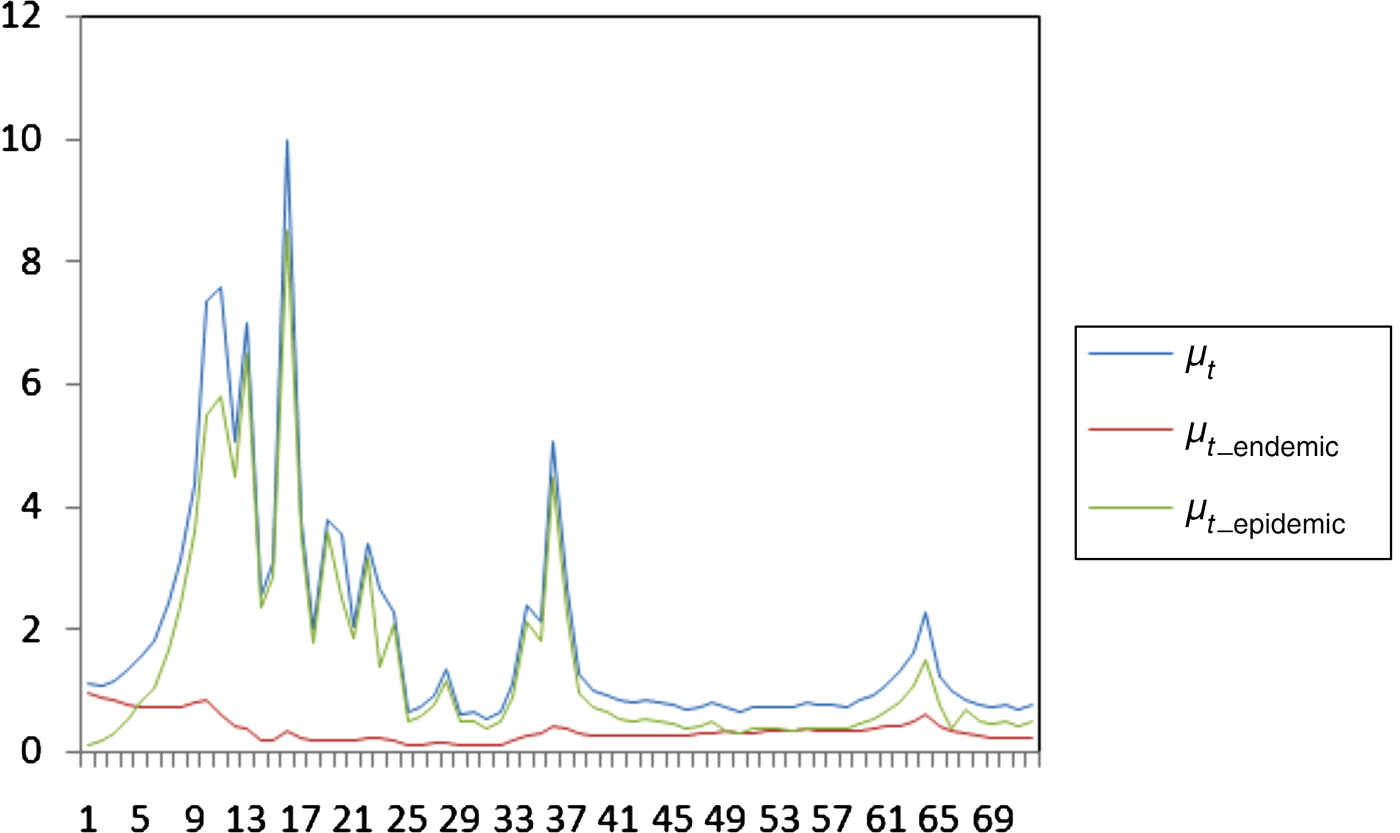
Fig. 2. Temporal evolution of μ t, μ t_endemic and μ t_epidemic during the 2000 foot-and-mouth disease outbreak.
Model posterior predictive checking
The predictive accuracy of our modelling has been evaluated by comparing the predicted infected farms obtained by the best selected model specification with the actual infected farms. The quality of the fit of the best model (ZIP) as suggested by the selection criterion was satisfactory, as revealed by Figure 3, where occurrence predicted values are plotted along with the observed occurrence data.

Fig. 3. Predicted vs. observed counts for the zero-inflated Poisson model (•, observed; - - - -, 95% probability intervals; –––––, predicted).
In particular, the distribution of infected cases appears to closely match the distribution of predicted occurrences.
DISCUSSION
FMD is not endemic in Greece. However, the country's prefecture of Evros has been considered as potential gateway of introduction and spread of FMD in Europe [Reference Branscum5, Reference Leforban and Gerbier22] due to its geographical location, i.e. the natural border of Europe with Asia (Turkey). Hence, the need to provide all necessary tools for the effective and early control of sporadically occurring epidemics in the region. In this paper we propose suitably chosen stochastic spatio-temporal models to describe the spread of FMD. Our modelling framework extends similar approaches on analysing FMD data [Reference Choi4–Reference Chhetri, Perez and Thurmond6] in various ways. Specifically, we incorporate spatial information in the form of kernel functions and we adopt a g-prior approach to cope with potential multicollinearity problems associated with correlated predictors frequently met in such type of data. We show that utilizing suitable distributions for modelling excess zeros considerably improves model fit. Under this framework, the ZIP specification enabled the accurate description of the transmission of FMD in 2000 in northeastern Greece.
Few of the candidate variables were important predictors for the occurrence of FMD (Table 3). Importantly, none of the considered meteorological covariates was included in the final model. Meteorological covariates were also proved in [Reference Choi4] to be non-significant for FMD occurrences. This lack of importance for covariates related to the airborne spread of the disease suggests that the main route for the epidemic was direct contact between animals through short/long distances. Although there are small differences in the fit of the models with different kernels, the slightly better performance of the fat-tailed kernel (A) indicates that long distance infections are not unlikely.
Conversely, the parameters accounting for spatial information were statistically significant. This result is generally robust, in the sense that sensitivity analysis conducted by changing the durations of incubation period (from the 14-day period recommended by the OIE to 1 day) did not show differences in the obtained outcomes. Moreover, it has been widely proclaimed in the relevant literature (see [Reference Keeling13, Reference Alexandersen23, Reference Hugh-Jones24]) that farm size is a key factor in the transmission of FMD as is the type of farm (e.g. cattle, sheep or mixed). The analysis of the current FMD epidemic data confirms this evidence and both the size and type of farms were important. Indeed, cattle (and, to a lesser extent, sheep) density is a statistically important predictor for the excess zero occurrence of the disease in agreement with the findings of other studies [Reference Keeling13, Reference Diggle25, Reference Tildesley26], that have shown that infectiousness increases as the number of animals (cattle) in the infected farms increase. Further, in line with our findings, Jewell et al. [Reference Jewell7] reported that individual cows were more likely to transmit FMD and also likely to be more susceptible to FMD than individual sheep.
The increased significance of cattle in FMD spread, compared to small ruminants such as sheep/goats can be attributed to several reasons. Clinical signs of FMD are more easily detectable in cattle than in sheep, where signs of the disease are very difficult to detect [Reference Gibbens27]. Generally, the dairy breeds of Europe, such as those of Evros prefecture, are characterized by severe clinical signs after infection with FMD virus, contrary to the typical breeds in Asia or Africa, where the signs are less obvious. Moreover, most frequent clinical examinations on organized cattle farms or the larger quantities of virus shed by cattle in their close environment may be associated with the relative importance of cattle in terms of spreading the disease, in comparison to sheep/goat farms [Reference Dadousis28] stresses the high infectiousness of cattle during the 2000 epidemic in Evros accompanied by the fast transmission of disease from animal to animal. Another characteristic of the specific Evros epidemic, is that signs of FMD infections were mostly detected in cattle. Only a few cases of infections in sheep have been reported to the authorities. Hence, this specific outbreak was mainly driven by epidemic rather than endemic factors as is generally expected for FMD cases. The latter implies that disease transmission occurred mainly due to animal-to-animal contact rather than survival of the FMD virus in contaminated environments and spread of the infection through indirect contact. From Figure 2 it is clear that the course of the infection rate is almost similar to the epidemic part indicating the trivial contribution of the endemic part.
CONCLUSION
We propose a stochastic spatio-temporal modelling approach that extends existing approaches in various ways, by accounting for ‘excess zeros’, incorporating spatial information and autoregressive-type stochasticity and addressing multicollinearity in the covariates. Our modelling framework considerably improved model fit on the FMD data in comparison to previous approaches. The association between FMD occurrence and covariates suggests that farm locations, as well as the type and size of the infected farms (epidemic component) is significant for the spread of an FMD epidemic rather than meteorological covariates (endemic component). Our modelling approach could be readily applied to other infectious diseases, thus providing insights to government agencies, and all those involved in the livestock industry for the prevention of acute epidemics such as FMD.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S095026881600087X.
ACKNOWLEDGEMENTS
This paper is dedicated to the loving memory of our friend and colleague Professor Zafeiris Abas.
DECLARATION OF INTEREST
None.







