INTRODUCTION
Dengue is one of the most serious mosquito-borne viral diseases, and major outbreaks have repeatedly occurred in the tropics and subtropics. Japan experienced dengue outbreaks during the Second World War; these outbreaks were recorded in southwestern Japan in the Kagoshima, Kumamoto, Nagasaki, Fukuoka, Hiroshima, Hyogo, Osaka and Mie prefectures [Reference Kurihara1, Reference Gratz2]. Of these, the largest outbreak was recorded in Nagasaki in 1942, in which 10% of the total population was reported to be symptomatic [Reference Hotta3]. Although dengue is not a public health concern in Japan at present, annual mean temperature has gradually been increasing [4] and Aedes albopictus, the vector, has expanded its infestation range northwards [Reference Kobayashi5] in recent decades. Millions of people now travel to Japan and other countries where dengue fever is endemic. Moreover, the number of imported dengue cases is on the rise [6], increasing the possibility of its re-emergence in Japan.
In mosquito-borne diseases, including dengue, the presence of the vector is necessary, but not sufficient, to cause epidemics. Outbreaks occur when vector density exceeds a certain transmission threshold, which is determined by factors such as ambient temperature and herd immunity level [Reference Focks7]. The Japanese population was considered naive to dengue prior to the outbreaks in the 1940s; the probable vector density that caused the outbreaks can be quantified based on the reported number of cases by simulating both the seasonal change in vector population and the effect of temperature on vector competence. Density is usually defined as quantity per unit measure, but we used the term differently; in this study, vector density indicates the number of female mosquitoes per person (MPP). MPP is an important indicator of the epidemic potential of dengue because the basic reproductive number (R 0) is directly proportional to MPP in mosquito-borne diseases in cases where the biting rate of the vector is steady. R 0 is defined as the expected number of secondary cases produced by the index case in a naive population during the entire period of infectiousness. When R 0 ⩾ 1, transmission is maintained and spreads in the population; conversely R 0 < 1 indicates that transmission declines and ceases.
It must be noted that A. albopictus was the principal vector in the 1940s outbreaks in Japan [Reference Hotta3], whereas, Aedes aegypti is commonly the principal dengue vector in the tropics and subtropics. A. aegypti is highly domesticated and exhibits strong anthropophilia [Reference Patz8, Reference Halstead9]; the human biting rate (HBR; number of bites given to humans per cycle/expected number of bites per gonotrophic cycle) of this species is approximately 100%. Unlike A. aegypti, A. albopictus is relatively exophilic, feeding on various kinds of hosts [Reference Hawley10]; finding and feeding on human hosts at every gonotrophic cycle is not easy for A. albopictus. It is likely that the HBR of A. albopictus is lower than that of A. aegypti, although the exact numbers are unknown.
Vector mortality is another important entomological parameter that influences the efficiency of viral transmission in mosquito-borne diseases [Reference Luz11]. However, the mortality rate of A. albopictus is not well understood. In previous studies, the reported average lifespan of A. albopictus varied widely from 2·7 to 20 days [Reference Hawley10, Reference Lacroix12].
The 1942 outbreak is considered the first dengue outbreak in Nagasaki; thus, all cases would be primary infections. Unfortunately, there is no serological data for the prevalence of anti-dengue antibodies in the population in Nagasaki. It is still unclear what proportion of infected individuals displayed clinical symptoms of dengue. Studies performed in areas where dengue is endemic and vectored principally by A. aegypti show that only a small proportion of primary infections are symptomatic; however, this can vary between 0 % and 70% [Reference Favier13, Reference Beckett, Kosasih and Faisal14].
The importance of A. albopictus as a dengue vector is increasing because this species is currently the most invasive mosquito worldwide [Reference Benedict15]. The presence of A. albopictus was first reported in 2004 in France and Croatia [Reference La16, Reference Gjenero-Margan17], and just 6 years later, autochthonous dengue infections vectored by A. albopictus were reported in both countries [Reference La16, Reference Gould18]. Thus, we believe that it is important to assess the vector competence of A. albopictus and estimate the number of female A. albopictus per person that caused a large dengue outbreak in the past. This may provide some perspectives towards reducing the dengue epidemic potential not only in Japan but also in those other temperate regions where A. albopictus can be the main source of dengue transmission.
In the present study, we aimed to estimate the probable vector density per person that caused the Nagasaki dengue outbreak in 1942 by using a mathematical model for dengue transmission dynamics based on the reported number of symptomatic cases. For uncertain parameters such as proportion of symptomatic cases, vector mortality rate, and HBR of A. albopictus, we applied various assumptions for the simulations.
METHODS
The model
We created a susceptible-exposed-infectious-recovered (SEIR) model of dengue virus transmission in a closed population; the equations are presented in Table 1. All parameters and their values are summarized in Table 2.
Table 1. Equations for the changes in each class of human and vector populations

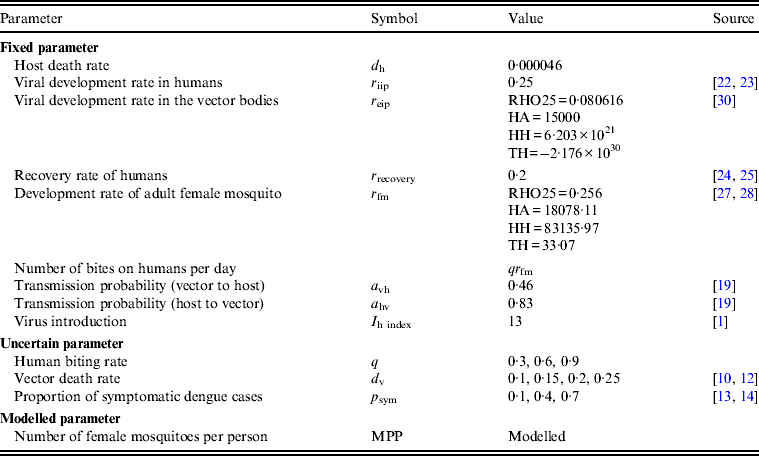
Table 2. Parameters and parameter values

RHO25, Development rate at 25°C; HA, enthalpy of activation of the reaction catalysed by the critical enzyme; HH, enthalpy change with high-temperature inactivation of the enzyme; TH, temperature at which 50% of the enzyme is inactivated.
Dengue virus
As our aim was to simulate the primary outbreak in a naive population, we employed only one dengue virus in our model. The virus was introduced into the population by the index case (I h_index); I h_index was assumed to be infectious on the day of arrival, and was not included in the resident population.
Transmission probabilities
Recent meta-analysis by Lambrechts et al. indicates that A. albopictus of ⩽5 generations in a laboratory colony possess a slightly higher oral receptivity of dengue virus (transmission probability from hosts to vectors: a hv) [rate difference (RD) = 0·08] and a lower infectivity (transmission probability from vectors to hosts: a vh) (RD=−0·29) than A. aegypti [Reference Lambrechts, Scott and Gubler19]. Applying these RD values on the generally accepted parameters for A. aegypti (0·75 for both a hv and a vh [Reference Newton and Reiter20]), we derived 0·83 and 0·46 for a hv and a vh, respectively, for A. albopictus.
Host population
The population of Nagasaki (N h) was 252 630 in 1940 [21]. We did not consider the distributions of age and sex. The host population was divided into S h (susceptible), E h (exposed), I h (infectious), and R h (recovered). We assumed that the entire population of Nagasaki was completely naive to dengue virus prior to its introduction; the initial values of S h, E h, I h, and R h were N h, 0, 0, and 0, respectively.
Mortality rate of humans
Human life expectancy was arbitrarily set at 60 years. The daily mortality rate of humans (d h) was 0·000046.
Viral development in the hosts
The intrinsic incubation period (IIP) was classically considered between 3–14 days (mean 5 days) [Reference Gubler22]. Eighty percent of biting experiments from host to vector successfully transmitted the virus even a day before becoming symptomatic [Reference Kuno23]. Hence, we adopted a constant value of 4 days for the IIP. The viral development rate in humans (r iip) was set to a constant value of 0·25.
Recovery rate of the hosts
The infectious period in the host was considered between 2 and 10 days [Reference Gubler22]. We assumed this value for 5 days in this model [Reference Gubler24, Reference Nishiura and Halstead25]. The recovery rate of humans (r recovery) was set to a constant value of 0·2.
Vector population
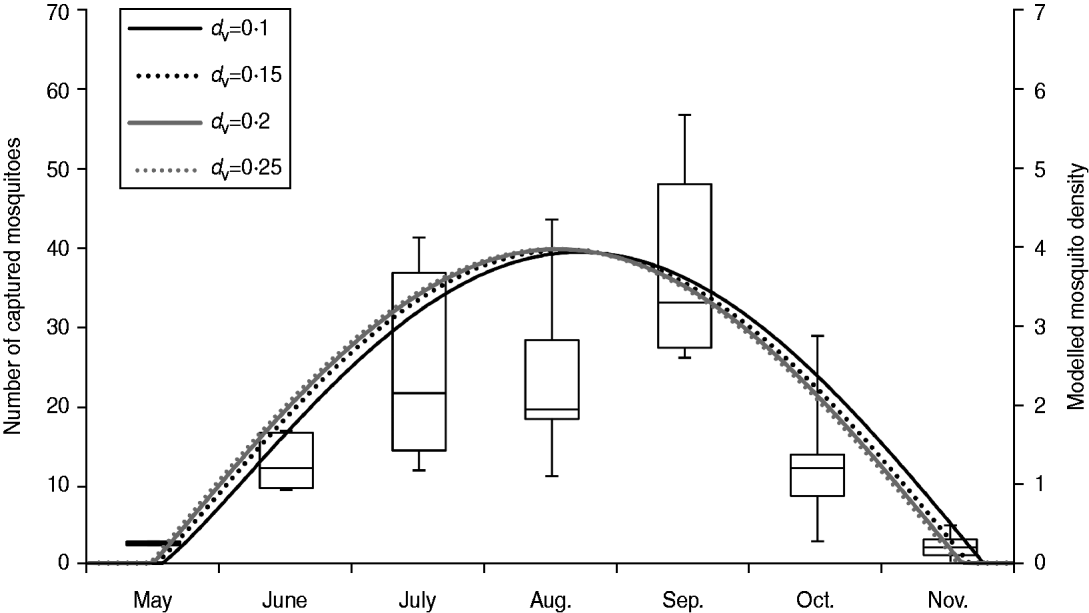
As male mosquitoes do not contribute to viral transmission, all the mosquitoes in our model were female mosquitoes. In Japan, the population of A. albopictus fluctuates seasonally and adult A. albopictus are usually found from May to November in Nagasaki [Reference Mori and Wada26]. Therefore, we assumed that mosquitoes were present only between 1 May (day 121) and 30 November (day 334) in our model. The peak mosquito population in a given year was determined by the product of the number of mosquitoes per person (MPP) and the human population (N h). Seasonal mosquito population (N v) on day t was mathematically modelled by a sinusoidal function as below, based on the field observation by Mori & Wada [Reference Mori and Wada26] (Fig. 1):
 $$\eqalign{\displaystyle{{dN_{\rm v}} \over {dt}}\tab = {\rm MPP}N_{\rm h} \sin \left[ {0.016882\left( {t + 240} \right)} \right]d_{\rm v} - N_{\rm v} d_{\rm v}\cr\tab \quad \quad \left( {121 \les t \les 334} \right),$$
$$\eqalign{\displaystyle{{dN_{\rm v}} \over {dt}}\tab = {\rm MPP}N_{\rm h} \sin \left[ {0.016882\left( {t + 240} \right)} \right]d_{\rm v} - N_{\rm v} d_{\rm v}\cr\tab \quad \quad \left( {121 \les t \les 334} \right),$$where d v is the vector mortality rate (see below).

Fig. 1. Seasonal changes in mosquito population. Left axis: box plot of monthly numbers of captured female A. albopictus during 1974–1976 in Nagasaki [Reference Mori and Wada26]. Right axis: seasonal changes in mosquito density [the number of female mosquitoes per person (MPP)] when the peak MPP = 4. d v is the vector mortality rate. Note that the original data from Mori & Wada [Reference Mori and Wada26] consisted of the number of female mosquitoes captured during 30 and 15 min in 1974 and 1975–1976, respectively. The data from 1974 was therefore divided by two for representation in this figure.
The vector population was divided into S v (susceptible), E v (exposed), and I v (infectious). Once infected, the vectors were assumed to possess lifelong infectivity. The initial value of S v, E v, and I v was 0.
Developmental rate of the gonotrophic cycle of adult female mosquitoes
The length of the gonotrophic cycle was calculated based on the temperature-dependent enzyme kinetic model described in a previous study [Reference Sharpe and DeMichele27]. The developmental rate of adult female mosquitoes (r fm) at temperature T (°C) was calculated by using the following equation:
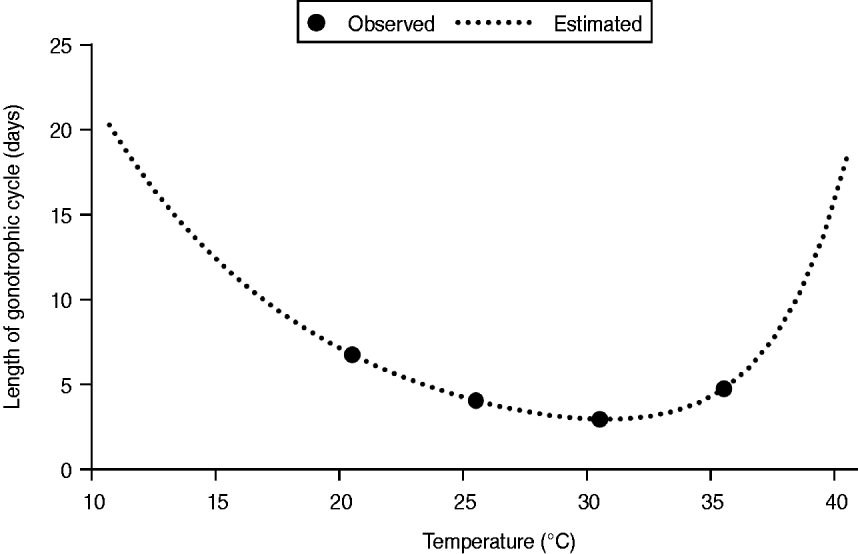
where, RHO25 is the development rate at 25°C without any temperature inactivation of the enzyme; HA (cal/mol) is the enthalpy of activation of the reaction that is catalysed by the critical enzyme; HH (cal/mol) is the enthalpy change with high-temperature inactivation of the enzyme; TH (°C) is the temperature at which 50% of the enzyme is inactivated at high temperature; R is the universal gas constant (1·987 cal/mol per degree). The values for RHO25, HA, HH, and TH for r fm in A. albopictus were not provided in previous studies. On the basis of the observed length of the gonotrophic cycle of A. albopictus [Reference Delatte28], we estimated the parameters for r fm by using a curve-fitting method [Reference Nelder and Mead29] (Fig. 2). The parameterized values of RHO25, HA, HH, and TH for r fm are 0·256, 18078·11, 83135·97, and 33·07, respectively.

Fig. 2. Estimated length of the gonotrophic cycle using the curve-fitting method.
Viral development in the vectors
The extrinsic incubation period (EIP) is known to change seasonally as a function of temperature [Reference Focks30, Reference Watts31]. We also applied equation (2) to calculate the temperature-dependent developmental rate of dengue virus in the vectors (r eip). The EIP in A. albopictus is considered to be equivalent to that of A. aegypti based on recent meta-analysis [Reference Lambrechts, Scott and Gubler19]. Thus, parameters for r eip were substituted with previously reported values for A. aegypti: RHO25 = 0·080616, HA = 15000, HH = 6·203 × 1021, TH=−2·176 × 1030 [Reference Focks30].
Uncertain parameters
HBR
The HBR (q) is defined as the quotient of the number of successful blood meals on humans and the expected number of bites per gonotrophic cycle. A. albopictus usually consumes a single blood meal per cycle [Reference Mori and Wada32], hence, the expected number of bites should be 1. We set q at various levels for exclusive (0·9), moderate (0·6), and limited (0·3) biting, respectively. The daily number of bites given to humans per mosquito was determined by the length of gonotrophic cycle and the HBR, and calculated by qr fm.
Mortality rate of adult mosquitoes
The mortality rate (d v) of A. albopictus was set at various levels between 0·1 and 0·25 with increments of 0·05. The mortality of this species is relatively steady while ambient temperature is optimal for its survival [Reference Delatte28], and it increases significantly at temperatures of <10°C or >35°C [Reference Ishii, Nakayama and Ishii33]. Thus, we assumed that d v was constant at a range of 10–35°C, and that all mosquitoes will die within a day (d v = 1) when the temperature is <10°C or >35°C.
Proportion of symptomatic dengue cases
The proportion of symptomatic cases (p sym) was set at 0·1, 0·4, and 0·7. The daily incidence of symptomatic cases was calculated by the equation: p symE hr iip.
Simulation
We obtained the recorded monthly temperatures of the city for 1942 [4] and converted them into daily values by interpolation. Precipitation, humidity, and diurnal length were assumed to be optimal to allow the survival and emergence of mosquitoes.
Estimation of the probable MPP
The time-course of the 1942 Nagasaki outbreak is well-documented [Reference Kurihara1]. It is reported that at least 13 dengue cases arrived at Nagasaki on 4 July. Subsequently, the first two domestic cases were recorded in a week, which rose to nine after a month. The reported cases increased to 2259 by the end of August, and further increased to 13323 by early October. In total, 23338 cases were recorded by the end of the year.
As reported, we conducted our simulation by introducing 13 infectious individuals (I h_index) into the city on 4 July 1942. Simulations were initiated with MPP = 1·0. We changed MPP at increments of 0·1, and calculated the cumulative number of domestic symptomatic cases with various assumptions of q, d v and p sym until 31 December 1942. The likelihood of our estimates reflecting the reported cases was evaluated at 5 points by using the least squares method. The MPP that resulted in the best fit was defined as the probable MPP. We fitted the cumulative number of symptomatic cases for the simulation because of the limitation of data availability. As the Nagasaki outbreak occurred over 70 years ago during the war, daily, weekly, or monthly incidence was unavailable.
We also calculated R 0 using the estimated MPP by the following R 0 equation for dengue [Reference Yang34, Reference Oki and Yamamoto35]. As R 0 is a point estimate, we representatively calculated R 0 on the virus introduction day (4 July 1942) while ambient temperature was 24·3°C.
Sensitivity analysis
To evaluate the impact of the parameters on our findings, we performed univariate, and multivariate sensitivity analyses by modifying the value of each parameter [Reference Luz36]. In univariate sensitivity analysis, the values of a hv, a vh, q, d v, d h, r eip, r iip, r recovery, p sym, and I h_index were modified to increase by 1%, and the change in total number of cases was then calculated. In multivariate sensitivity analysis, these parameters were randomly sampled 1000 times at 25% above and below their baseline values. We obtained 1000 estimates of the cases followed by a multivariate linear regression analysis to investigate the parameters that most strongly affected the model. Significance was set at 0·01.
RESULTS
The probable MPP in the Nagasaki dengue outbreak in 1942 with various assumptions of q, d v and p sym are presented in Table 3.
Table 3. Probable number of Aedes albopictus per person during the Nagasaki dengue outbreak in 1942

When the exclusive HBR (q = 0·9) was assumed, the probable MPP was estimated as between 15·0 and 62·4. When the HBR was assumed to be moderate (q = 0·6), the higher probable MPP was estimated between 33·8 and 140·0. When the limited HBR (q = 0·3) was assumed, the estimated MPP was much higher, between 135·1 and 558·0.
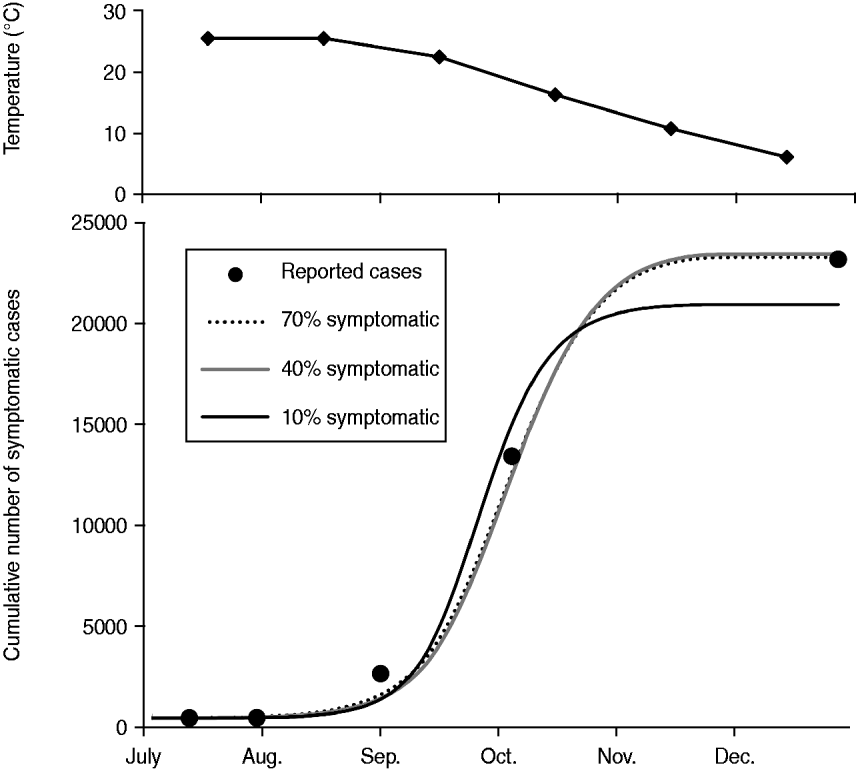
When the most favourable conditions for disease spread were assumed, such as a combination of the exclusive HBR (q = 0·9) and the longest vector survival (d v = 0·1), MPPs of 15·0, 16·9, and 25·1 were required to cause the Nagasaki outbreak if 70%, 40%, and 10% of infected people were symptomatic, respectively (Fig. 3). When the most unfavourable conditions for disease spread were assumed, such as a combination of limited HBR (q = 0·3) and highest vector mortality (d v = 0·25), the probable MPP appeared to be extremely high, i.e. 367·1, 405·2, and 558·0 at p sym = 0·7, 0·4, and 0·1, respectively.

Fig. 3. Simulation results showing monthly mean temperature in Nagasaki in 1942 and the best fit simulations when the longest vector survival (d v = 0·1), and the exclusive human biting rate (q = 0·9) are assumed. By using the least square method, the number of mosquitoes per person (MPP) was estimated to be 15·0, 16·9, and 25·1, while the proportion of symptomatic cases was assumed to be 0·7, 0·4, and 0·1, respectively.
Overall, the probable MPP increased with an increase in d v, and it decreased with an increase in q and p sym.
The estimated R 0 values on 4 July are given in Table 4.
Table 4. Estimated R0 during the Nagasaki dengue outbreak in 1942

Sensitivity analysis
The reference value for the total number of cases is 23445, which was estimated at q = 0·9, d v = 0·1, and p sym = 0·7, with MPP = 15·0. In the univariate sensitivity analysis, the parameter that most strongly affected the number of cases was q; there was a 10·1% increase with a 1% increase in q. The parameters with the subsequent strongest effects were a vh and a hv. The total number of cases increased by 4·9% with a 1% increase in a vh and a hv. This was followed by d v, where the total number of cases decreased by 4·2% with a 1% increase in d v. In the multivariate sensitivity analysis, the parameters that significantly affected total number of cases were q, a hv, a vh, d v, r eip, r iip, and r recovery.
DISCUSSION
In the present study, we attempted to estimate the probable number of A. albopictus per person that triggered the largest dengue outbreak in Japan, using a mathematical model that incorporated temperature-dependent developmental rate of the vector mosquito and dengue virus. We applied various assumptions for uncertain parameters such as the proportion of symptomatic cases, mortality rate, and the HBR of A. albopictus. Our results show that the probable MPP is a very high value between 15·0 and 558·0. When the most favourable condition for disease spread, such as a combination of the exclusive HBR and the longest vector survival was assumed, a MPP of at least 15–25 was required to cause the 1942 Nagasaki outbreak. A much higher MPP was required to trigger the outbreak if HBR was lower, and/or the vector lifespan was shorter. The trend showed that the probable MPP increased with increasing mortality rate, and decreasing HBR and proportion of symptomatic cases. The estimated R 0 in the Nagasaki outbreak was between 6·1 and 13·9 in all settings.
The length of the gonotrophic cycle of A. albopictus was estimated to be 3–4 days between July and September by equation (2). Although the probable MPP was estimated to lie in a broad range, even a MPP of 15–25 appears to be a high density as this is almost equivalent to 4–8 mosquito bites per person per day if the HBR of mosquitoes is exclusive. The actual vector density during the 1942 Nagasaki outbreak is unknown, but it must have been very high as described in a report of the time in the following manner: ‘Aedes albopictus was dancing everywhere and an uncountable number of larvae was found in the outside water tanks’ [Reference Hotta3]. Since Japan was at war in 1942, large numbers of water tanks were located around the houses for preventing fires resulting from bombings, and the tanks were considered as important mosquito breeding sites [Reference Gratz2]. Presumably, this extremely high vector density was the most critical causal factor of the Nagasaki outbreak. In addition, most of the houses did not have window screens, and windows were usually left open for ventilation in summer which provided the mosquitoes with easy access to the houses. People tended to go outside to enjoy the cool breeze in the evening, allowing A. albopictus to easily consume a blood meal on humans [Reference Hawley10]. The traditional Japanese lifestyle and human behaviour were likely to increase the frequency of mosquito–human contacts in and around the houses. The HBR of A. albopictus at that time could be assumed to be almost as high as that of A. aegypti. As our result indicated, the required mosquito density to cause the Nagasaki outbreak was estimated unrealistically high at more than 100–500 mosquitoes per person, if the limited HBR (q = 0·3) was assumed in the simulation (Table 3).
In present-day Japan, such water tanks no longer exist, but a new problem has arisen with regard to potential mosquito breeding sources in urban and suburban areas. There are several catch basins at the bottom of rainwater drainage systems around houses. These catch basins maintain rainwater for several days or weeks following rain, and have recently been implicated as one of the main sources for mosquito breeding. Although A. albopictus is known to be an omnivorous mosquito, it exhibits a relatively high anthropophilic feeding pattern in urban and suburban areas in Japan [Reference Sawabe37]. Therefore, this is an important problem in the context of public health because a high vector abundance in residential areas with a high density of susceptible hosts is clearly undesirable for the prevention of mosquito-borne diseases.
Although a higher vector density can be observed focally where breeding sources are particularly abundant, we believe that the current density of A. albopictus is significantly less than the extremely high density described in the earlier report. On average, a Japanese individual is bitten less than once a day by A. albopictus (data not shown). Most Japanese houses and buildings now have an airtight structure with intact window screens; such structural features help prevent the entry of A. albopictus [Reference Higa38]. Nearly 90% of households contain air conditioners [39], and people tend to stay indoors during the summer. Additionally, several effective repellents and insecticides are available in the market and many people use repellents both indoors and outdoors. We expect that such changes in the living environment, coupled with human behaviour would considerably decrease contact frequency with mosquitoes, regardless of density [Reference Reiter40].
However, we could not directly compare the vector densities between the earlier outbreak and the present, since the actual density of A. albopictus in the natural environment still remains unknown. Although conducting entomological field surveillance is beyond the scope of this study, it is one of the study's limitations; it is important to investigate if the vector density in present-day Japan is definitively lower than the threshold for the prevention of the re-emergence of dengue.
Several studies attempted to estimate R 0 values in dengue outbreaks in areas where dengue is vectored by A. aegypti. R 0 was estimated as 2·0–103 in Brazil [Reference Favier41], 0·49–3·30 in Mexico [Reference Chowell42], 1·89–2·23 in Singapore [Reference Hsieh and Ma43], and 3·93–4·67 in Taiwan [Reference Hsieh and Chen44]. Our estimated R 0 (6·1–13·9) was relatively high but compatible with these values. Nishiura indicated that the proportion of asymptomatic cases should be taken into consideration in the estimation of R 0 [Reference Nishiura45], and our result revealed that R 0 was higher when the majority of infected individuals were asymptomatic (Table 4).
Our study has a number of other limitations. First, due to the deterministic nature of our model, stochastic phenomena involved in the real world transmission dynamics could not be depicted in this study.
Second, the presence of A. albopictus was determined based on seasonality in this model (Fig. 1). We incorporated the effects of ambient temperature on the development and survival of mosquitoes; however, various seasonal climatic factors other than temperature also influence mosquito population dynamics in nature. Precipitation determines breeding site availability, and diurnal length induces egg diapause [Reference Mori, Oda and Wada46]. These factors were assumed to be optimal for emergence and survival of the vector in this model. However, if the effects of these climatic factors were additionally incorporated, they may affect our findings since seasonal mosquito population fluctuations are more complex.
Third, we assumed a slightly lower viral transmissibility of A. albopictus in this model on the basis of a recent meta-analysis [Reference Lambrechts, Scott and Gubler19]; however, the vector competence of A. albopictus, and its comparison with that of A. aegypti is debatable [Reference Chen47–Reference Vazeille49]. As shown by our sensitivity analysis, if the actual values of transmission probability (a vh and a hv) are very different from our assumption, it strongly affects the value of the probable vector densities.
Fourth, we assumed a constant mortality rate of mosquitoes within a viable temperature range (10–35°C), with the rate markedly increasing when the temperature was out of range. The optimal temperature for mosquito survival is believed to be between 15°C and 30°C [Reference Delatte28]. The effect of temperatures in the range of 10–14°C, and 31–35°C on mortality rate is uncertain. If the mortality rate increases at these suboptimal temperatures, our assumption may be overly simplistic to describe the actual survival ability of mosquitoes.
Fifth, our model does not include spatial heterogeneity of vectors and hosts. According to the 20–80 rule in vector-borne diseases, 20% of the host population is responsible for 80% of net transmission [Reference Woolhouse50]. In fact, it has been reported that 70–75% of reported dengue cases occur in limited areas where vector mosquitoes are abundant, and/or several susceptible hosts are clustered together [Reference Burattini51, Reference Barrera52]. However, we assumed that the transmission takes place homogeneously in the entire population in this model.
Despite these limitations, our study highlights that the unusually high vector density due to wartime practices and the traditional Japanese lifestyle were principally responsible for the Nagasaki dengue outbreak in 1942. We do not deny the possibility of re-emergence of dengue outbreaks in present-day Japan, since A. albopictus is still abundant. However, in the event of a recurrence, it is likely that the outbreak will remain focal and not spread as much as the earlier one, since circumstances have changed leading to a modern lifestyle and protective human behaviour.
Finally, we emphasize that there are still several entomological uncertainties with A. albopictus as a dengue vector. Future research is required to evaluate the risk of the diseases such as dengue and chikungunya that are transmitted by this species in Japan and other countries where A. albopictus is present, but epidemics have not yet occurred.
ACKNOWLEDGEMENTS
The authors thank Toshihiko Sunahara, Institute of Tropical Medicine, Nagasaki University, for his technical support with model development. This study was supported by grants from the Ministry of Education, Culture, Sports, Science and Technology and the Global Center for Excellence Program of the Ministry of Education, Culture, Sports, Science and Technology. No funding bodies had any role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
DECLARATION OF INTEREST
None.