INTRODUCTION
Acute respiratory illnesses (ARIs) stand out as the most common health complaint worldwide [Reference Monto1]. They were estimated to cause 4·2 million deaths and 97 million disability adjusted life years (DALYs) in 2004 [Reference Monto1, Reference Mathers, Fat and Boerma2]. The usual syndrome consists of malaise, headache, myalgia, sore throat, coryza, fever, cough, dyspnoea and additional signs of respiratory distress; clinical abnormalities generally arise in that order as severity of disease increases [Reference Doyle, Cohen, Eccles and Weber3, Reference Carrat4].
Although bacteria may be present primarily or as a complication, it is viruses that cause ARIs most commonly (70–90% of cases). Over 200 different causal viruses have been identified, but most ARIs stem from rhinovirus, respiratory syncytial virus (RSV), coronavirus, adenovirus, metapneumovirus, and influenza or parainfluenza viruses [Reference Mathers, Fat and Boerma2, Reference Nokso-Koivisto5–Reference Pica and Bouvier8]. Public health impact of diseases from different viruses is distinct, and more attention has been devoted to those posing higher threats, such as influenza and RSV, through the former's potential for high-mortality pandemics, and the latter's more severe expression in children, often involving the lower airways.
In community settings most cases are mild, and the fraction of patients that seeks medical care usually receive symptomatic treatment without inquiry into the aetiological agent or agents, due to practical and financial constraints. Counts of ARI cases are kept and published in states that are members of the World Health Organization (WHO), and are used to report on global health and health-related economics [Reference Mathers, Fat and Boerma2]. These counts represent a proportion, likely to vary with age group, gender, and severity, of the real number of cases.
ARIs are related to weather; their name in many languages reflects this age-old observation (English: cold; Spanish: resfrío; German: Erkältung; French: froid). Indeed, counts of cases in temperate climates show peaks during their cold, dry, and low solar-radiation winters. On the other hand, tropical climates display an ARI incidence pattern with highs in the rainy season, during their warm summer [Reference Tamerius9–Reference Roberts and Kiang12]. It is of note that for some pathogens capable of causing ARIs, a biennial rhythmicity has been described (RSV, metapneumovirus, parainfluenza) in temperate regions; still, the seasonal variation of ARIs in general is annual [Reference Tamerius9, Reference Walton13].
There have been efforts to quantify the relationship between ARIs and weather. Laboratory and observational studies suggest the existence of effects of low and high meteorological parameters for a variety of viruses on (1) the amount and viability of viruses shed by diseased individuals, (2) the probability of successful transmission by different mechanisms, and (3) host states that determine an individual's immunity and the group's vulnerability to an epidemic. Doyle & Cohen [Reference Doyle, Cohen, Eccles and Weber3] observed that for viruses such as RSV or influenza, temperature, relative humidity, barometric pressure and ultraviolet radiation can explain 40% of the variance in the risk of ARI, and interpret this literature finding as related to the physical conditions favouring virus survival. Indeed, technical reports such as the one by Roberts & Kiang [Reference Roberts and Kiang12] on seasonal influenza transmission classify the meteorological factors recorded in the literature as those affecting virus survivorship (higher temperature, humidity, vapour pressure, and solar irradiance all decrease virus survival), those affecting transmission efficiency (decreased by higher temperature and vapour pressure, increased by higher rainfall, by ENSO, more air travel and holidays, and with varying reports for humidity), and those affecting host susceptibility (decreased by higher sunlight exposure and with varying effects of nutrition). It is likely that the weather's influence on ARIs is mediated at least partially by effects on contact rates, and such effects may vary by type of climate and cultural group, as suggested by empirical observations [Reference Mathers, Fat and Boerma2, Reference Wong-Chew6, Reference Pica and Bouvier8, Reference Brankston14].
Our study used data from a primary-care population in the state of Nuevo León, in northeastern Mexico. Nearly four million inhabitants (about 80% of the state population in 2010) live in the metropolitan area of Monterrey, 537 m above sea level, and ∼270 km north of the Tropic of Cancer. The climate is semi-arid (Köppen classification BSh), with a long hot season (>32°C monthly average of daily maximum, individual readings as high as 45°C, 2004–2010), correspondingly short cool and cold seasons, scarce precipitation (between 0·94 mm and 228·6 mm per day, mostly during the summer), and mild winters (between 4·5°C and 7·4°C annual average of daily minimum). During winter, the region experiences sudden changes in temperature, which may fall by 20°C in a few hours, often accompanied by high humidity and generalized low-intensity rain.
This paper describes a vector error correction model with covariates (VECMX), that relates weekly counts of ARIs in a primary-care setting to weather variables in a specific climate, that of the northeast of Mexico, using data from 2004 to 2010. Models such as the one reported here may provide quantitative support for the role of contact rates in epidemic spread in naturalistic settings, by comparing the weather most likely to make people stay indoors in different cultures. If similar degrees of explanation are attained through the use of different weather variables in contrasting climates and peoples, human behaviour would be the parsimonious explanation. If, on the other hand, the same weather variables are related to increases in counts of cases worldwide, biophysical effects on viruses, hosts and groups should be attested to as more efficiently promoting the rapid dissemination of disease.
METHODS
Weekly ARI counts
The Universidad Autónoma de Nuevo León's (UANL) 11 primary-care clinics in the municipalities of Apodaca and Guadalupe, within the Monterrey metropolitan area, provide medical care in low-income neighbourhoods. The data included weekly counts of the ICD-10 diagnoses listed in Table 1 (chronic ailments were excluded), as well as the age in years and the gender of the patient. Table 2 summarizes the demographical data of the sample.
Table 1. ICD-10 codes and clinical diagnosis scored as acute respiratory illnesses
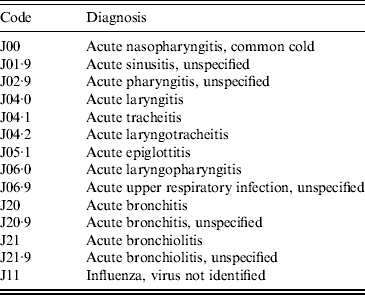
Table 2. Gender and age group of patients in the acute respiratory illness counts (2004–2010)
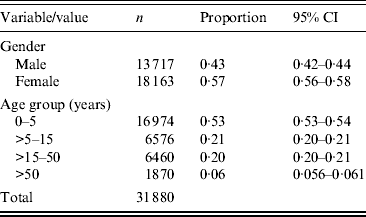
CI, Rounded confidence interval.
Weather data
The study used information from the ‘Monterrey’ weather station (100° 16′ 18″ longitude, 25° 40′ 57″ latitude) for the same years, accessed through the National Water Commission (CONAGUA) website [15]. The readings consisted of mean temperature, maximum temperature, minimum temperature, barometric pressure, relative humidity, wind velocity, wind direction, and rainfall. After exploratory analysis, only the series of observations constituted by three parameters, i.e. minimum temperature during a given week, median of the observations of relative humidity during a given week, and rainfall accumulated during a given week, were retained in the model.
Statistical methods
Database conditioning
(a) Case count database
In order to correct for the bias introduced by non-biological variations in case counts, probably due to changes in the administrative organization of healthcare institutions affecting the number of persons served, such as the introduction of a new federal programme in 2004 known as Seguro Popular (Popular Insurance), the counts of cases for 2004–2006 were scaled using state-wide data published by the State Health Ministry (Secretaría de Salud de Nuevo León), preserving the overall dynamics of the series. In addition, these Poisson counts were transformed to stabilize their variance and to smooth them, by Y = 2[y ½] [Reference Bickel and Doksun16]. In addition, the demographic covariables were standardized, to render them less prone to noise from variation in the number of persons seeking attention related to administrative or political factors.
(b) Meteorological database
A small amount of observations (52/1092, 4·5%) were missing or clear errors (e.g. temperatures incompatible with life, relative humidity of zero accompanied by non-zero rainfall), and were substituted by estimates from a smoothing technique as proposed by Cleveland et al. in 1990 [Reference Cleveland17].
Model building
Weather variables modelling
As stated earlier, exploratory analysis led to inclusion in the model of three weather parameters: the minimum temperature during a week, the median of all readings of relative humidity in a week, and the weekly accumulated rainfall. As expected, variables in the meteorological database displayed linear and nonlinear dependencies, a situation known as multicollinearity. Regression procedures attempted with such data yield unstable and hard to interpret coefficients for the independent variables.
Therefore, we created a weather index through partial least squares (PLS) [Reference Geladi18]. PLS is a technique that exploits the dependency structure in a set of variables to determine a group of coefficients that best relate them to a dependent variable. PLS is similar to principal components analysis (PCA) and factor analysis (FA) in that they are all methods to reduce the dimensionality of a model by projecting a set of variables into a hyperplane that retains most of the information, but under different criteria. FA uses a model determined by the researcher, whereas PCA chooses a number of orthogonal dimensions based on maximizing the variance of the independent variables in each dimension, rendering it a more unspecific technique than PLS. PLS is also different in the fact that both the dependent and the independent variables are projected into a different space, with the aim of maximizing the covariance in them, as opposed to the unique variance maximization that occurs in PCA through the projection of one set of variables. The solution in PLS is a nonlinear function that is best suited for forecasting purposes. In our model, we were only interested in the coefficients of the solution produced, as a single index that captures the information in the three weather variables, and could be used in further statistical procedures [Reference Garthwaite19, Reference Janes and Yaffe20].
Vector error correction modelling
Multivariate time-series models undertake either the explanation or the prediction of the observations in one time-series by the dynamics of one or more other series that may summarize several variables. VECMXs are a subtype that seeks to do this by estimating: (1) long-term effects, (2) short-term or shock effects, and (3) an error term, which in a correctly specified model should be random noise. VECMXs allow the variables to ‘speak by themselves’, producing estimates of the long-term relationship between the time-series, decomposed in parameters of trend (how the series influence each other in the long term), seasonality (the time-frame in which oscillations around the trend are best understood), and autocorrelation [the extent of influence of the previous observation on subsequent one(s)] in the long-term relationship, and of the impact of sudden changes in the independent variables and covariates on the short-term relationship, including the speed with which the dependent series returns to the long-term relationship equilibrium [Reference Sims21]. In a problem such as the one we consider here, VECMX-relevant contribution is to determine if the dynamics present in the weather variables index are capable of reproducing the dynamics present in the ARI counts time-series.
Two covariates were included in the model. Age group and gender data were available for each case diagnosed, and were included since variations over time were observed on exploratory analyses. Once again, a PLS index for the proportions of each category allowed the addition of an age group covariate to the model. The gender covariate was added as the proportion of males. Since these primary-care clinics remained closed for 2 weeks for each Christmas and Easter holiday seasons, a covariable to adjust for these weeks, when zero cases meant that no patient requested attention, was also included. All these covariables were added because of particularities in the data, influenced by non-biological factors in this relatively small healthcare system, and thus will not be interpreted in the discussion of the model in epidemiological or biological terms.
We tested the fit of models with all combinations of three different parameters: trend (none, constant, positive), seasonality (3–52 periods), and lag (1–18 periods). It is of note that a VECMX model is able to provide spurious significance (regression artifacts), therefore the modelling procedure must include a diagnostic phase. In our model's development, residual hypothesis-testing including autocorrelation tests supported the selection of a group of models. They were later tested for co-integration, believed to occur when there is a unique relationship in the series that does not depend on time, through the maximum eigenvalue long-term test [Reference Johansen22–Reference Johansen, Andersen, Davis, Kreiss and Mikosch25]. From the models that remained after performing these diagnostics, we chose the one that maximized fit and plausibility.
Finally, we used an outlier Z test (α = 0·10) to detect atypical counts of cases that could not be explained by the model.
All the analyses were performed using the free open source statistical software R, specifically the packages ‘pls’ and ‘vars’ [26–Reference Mevik and Wehrens28].
RESULTS
Weather index
The PLS solution to the problem of the combination of weather parameters that maximizes the covariance with the case counts, produced the coefficients described in Table 3 and equation (1).
 $$\eqalign{ & {\rm PLS\ weather\ index} = -0\!\cdot\! 26\ {\rm minimum\, temperature}\cr&\quad{\rm in\, the\ week} + 0\!\cdot\! 22\, {\rm weekly\, median\, of\, relative}\cr&\quad{\rm humidity}+ 0\!\cdot\!5\, {\rm weekly\, accumulated\, rainfall}.} $$
$$\eqalign{ & {\rm PLS\ weather\ index} = -0\!\cdot\! 26\ {\rm minimum\, temperature}\cr&\quad{\rm in\, the\ week} + 0\!\cdot\! 22\, {\rm weekly\, median\, of\, relative}\cr&\quad{\rm humidity}+ 0\!\cdot\!5\, {\rm weekly\, accumulated\, rainfall}.} $$
The index is higher when the minimum temperature in the week is lower, and both weekly median of relative humidity and weekly accumulated rainfall are higher; the impact of rainfall is stronger than that of the other two parameters.
Table 3. Partial least squares (PLS) coefficients for weather index and age group index

Covariates
Age group index
The PLS coefficients are described in Table 3. The resulting index assigned a lower weight to the transformed number of diagnosed cases in children aged ⩽5 years, and assigned increasingly higher weights to those aged >50, >5–15, and >15–50 years, in that order. Gender was added as the proportion of males in the counts of a given week. It is important to remember that we introduced this type of covariable only as an adjustment device, due to the sample characteristics, and not for an epidemiological reason.
 $$\eqalign{ & {\rm PLS\ age\ group\ index} = (0\hskip-1.5pt \cdot \hskip-1.5pt24)\ 0\hskip-2pt - \hskip-2pt 5\,{\rm years} \cr & \quad + {\rm (}0 \hskip-1.5pt\cdot \hskip-1.5pt43{\rm )} \gt 5\hskip-2pt - \hskip-2pt15\,{\rm years} + (0 \hskip-1.5pt\cdot \hskip-1.5pt54) \gt 15\hskip-2pt - \hskip-2pt 50\,{\rm years} \cr & \quad + (0 \hskip-1.5pt \cdot \hskip-1.5pt 33){\rm} \gt 50\,{\rm years}.} $$
$$\eqalign{ & {\rm PLS\ age\ group\ index} = (0\hskip-1.5pt \cdot \hskip-1.5pt24)\ 0\hskip-2pt - \hskip-2pt 5\,{\rm years} \cr & \quad + {\rm (}0 \hskip-1.5pt\cdot \hskip-1.5pt43{\rm )} \gt 5\hskip-2pt - \hskip-2pt15\,{\rm years} + (0 \hskip-1.5pt\cdot \hskip-1.5pt54) \gt 15\hskip-2pt - \hskip-2pt 50\,{\rm years} \cr & \quad + (0 \hskip-1.5pt \cdot \hskip-1.5pt 33){\rm} \gt 50\,{\rm years}.} $$
VECMX
In the selected model, the maximum eigenvalue test rejected the first null hypothesis, namely, the lack of a time-independent relationship, and did not reject the second null hypothesis, that there could be only one such relationship. It showed a slight positive trend of 0·01; the long-term equation was also significant, with a coefficient of 1·69 for the weather index (P ⩽ 0·00). In the short-term equation, the week of the year (4·42, P = 0·01), having more older children and adults (1·50, P ⩽ 0·00), and less males (−2·43, P = 0·04), all had a statistically significant effect. The vector of short-term error corrections so formed was also significant (−0·67, P ⩽ 0·00), and the overall degree of explanation was 76% (adj. R 2 = 0·76; for the most important coefficients, see Table 4). As stated earlier, the relevant information in a VECMX model for a problem like the one studied here is to determine the ability of one series, the weather index series in this case, to reproduce the dynamics of the dependent series, the ARI counts in this paper; this is shown graphically in Figure 1. (The full VECMX equation and table of coefficients is available upon request.)

Fig. 1 [colour online]. Smoothed acute respiratory illness (ARI) series (black line) and model fit (grey line). Shaded areas in the background indicate the calendar autumn and winter seasons in each year.
Table 4. VECMX adjusted parameters

VECMX, Vector error correction model with covariates; PLS, partial least squares; n.a., not available.
Bold values indicate statistical significance (P ⩽ 0·05).
Finally, hypothesis testing characterized the residuals as random noise, and values in the uppermost 10% of the observations were defined as atypical (n = 14 weeks in the whole period, see Fig. 2).

Fig. 2 [colour online]. Weeks with atypical counts (outbreaks). 1 = week 51, 2004; 2 = week 13, 2005; 3 = week 51, 2006; 4 = week 1, 2007; 5 = week 6, 2007; 6 = week 8, 2007; 7 = week 36, 2007; 8 = week 42, 2007; 9 = week 1, 2008; 10 = week 15, 2008; 11 = week 17, 2009; 12 = week 36, 2009; 13 = week 12, 2010; 14 = week 15, 2010.
DISCUSSION
We report a VECMX, using commonly kept data and free open source software, to help explain the dynamics of acute respiratory infection counts in terms of the weather in an urban community.
As mentioned, PLS maximizes the covariance in the weather series of observations and the ARI counts. The best possible fit between the transformed counts and the new variable, the PLS weather index that combines the three weather series, is given by awarding a −0·26 weight to the minimum temperature during a given week, a 0·22 weight to the median of relative humidity during a given week, and a 0·5 weight, the heavier influence, to accumulated rainfall during a given week. The signs of the coefficients imply the direction of the relationship: negative for minimum temperature means that the lowest temperatures are responsible for the relationship, while the positive signs for the other two parameters indicate that the highest readings are the ones that bear relation to increases in counts. This is in keeping with the literature on the most common viral agents [Reference Tang7–Reference Tamerius9, Reference Soebiyanto, Adimi and Kiang11, Reference Walton13, Reference Chan29–Reference Grassly and Fraser33].
Both the gender and age-group PLS covariables render the dynamics of the influence of the weather index on the transformed counts clearer. It is known that young children are more vulnerable to ARIs and their complications than adults; and gender has been repeatedly proven not to affect the probability of ARI transmission ([3, p. 162, and references therein]). These covariables merely control for swifts in the covariances of the standardized demographic observations and the transformed counts of ARIs along time-lines. The statistically significant trend in the model is quite small and thus lacks epidemiological importance; it may reflect demographical growth, somewhat blunted since the large non-biological fluctuations in the number of visits to the clinics were corrected for, as explained in the Methods section. The modelled relationship of weather to the ARI counts does have further impact on the short-term relationship, where only the last 3 weeks have significant coefficients, all with a negative sign. In other words, there were more cases in week T when weeks T-1, T-2 and T-3 were characterized by high scores in the weather index, and when considering the dynamics of pairs of weeks, the previous one had a stronger influence (T-3 > T-2 > T-1), while this relationship diluted itself from T-4 onwards. However, the short-term relationship is characterized by a rather quick return to the long-term relationship, as can be inferred from the error correction coefficient of 0·67, meaning that 67% of the changes dissipate over a week. The proportion of the variability explained by the model is very satisfactory, 76% (adj. R 2 = 0·76), the highest we were able to locate in the literature, perhaps owing to its multivariate (as opposed to multiple) nature.
The fitted model has two interesting advantages that, to our knowledge, previously reported models have not provided: (1) it lends itself to replication in different types of climate and different countries, due to its widely available types of data input, and (2) it has a low cost of implementation.
The first difference pertains to what at first may seem a lack of sophistication in the model, which does not consider the different pathogens involved. Indeed, successful efforts to relate weather parameters to the incidences of specific viral pathogens in ARIs have been previously reported [Reference Tang7–Reference Tamerius9, Reference Soebiyanto, Adimi and Kiang11, Reference Walton13, Reference Chan29–Reference Grassly and Fraser33]. Laboratory and special population studies have shown effects of weather variables on the successful transmission by specific mechanisms for different viruses, affecting the length of time spent in the air for aerosol droplets, the survival of viruses on hands and objects, and the ability of the respiratory and immune systems to defend the individual from infection, among other parameters. Even though documented in laboratory conditions, the size of these effects in a naturalistic setting remains unclear.
It has been suggested that the weather's effect on contact rates is larger than the more biophysical virus-specific effects [Reference Mathers, Fat and Boerma2, Reference Brankston14]; further studies on the epidemiological dynamics of ARIs are needed to clarify the ‘efficiency’ of the effects to facilitate epidemics. In our opinion, models such as the one reported here may help to shed light on this issue. When adjusted for diverse climates and communities, they will determine if the kinds of weather that make a particular cultural group stay indoors, different for diverse latitudes and peoples, explain ARIs counts with a comparable degree of completeness. This possible result would weigh in favour of the increased contact rates explanation for the naturalistic spread of epidemics. On the other hand, the same modelling procedure may also be applied to carefully sampled counts of different aetiological agents, and thus inform specific prevention policy makers and their vaccination strategies [Reference Urashima, Shindo and Okabe30].
The model we report does not imply causality. The reasons why cold rainy weeks are consistently associated with higher counts of cases 1–3 weeks later in a semi-arid climate in Mexico are not shown in these data. Yet, the described procedure presents an advantage to healthcare systems of any size, complexity, or global localization: an affordable way to compare the weather's influence on ARIs across the world using commonly kept data and software that is freely available through the internet.
Still another feature in the model, useful for decision-making authorities, is the detection of atypically high numbers of cases. Epidemiological outbreak detection methods are in wide use, and the model provides a further check on this crucial public health function, which is so important because of the serious consequences of falsely reporting either an outbreak or its absence.
This set of procedures is easily reproducible for researchers throughout the world, and may add quantitative information about the means through which the weather influences the number of ARIs in different climates.
ACKNOWLEDGEMENTS
The authors thank Víctor Hugo Muñoz Sánchez, Ph.D. for his help in preparing the figures for this paper. This work was supported by the Consejo Nacional de Ciencia y Tecnología (CONACYT, grant no. 105657).
DECLARATION OF INTEREST
All of the authors hold academic or professional positions in public institutions and do not have any relationship with for-profit organizations, nor have any of them received an extraordinary stipend for the work hereby presented.







