INTRODUCTION
Campylobacter is one of the most common causes of infectious intestinal disease in the developed world. In England and Wales in 2009 there were 57 772 human cases of Campylobacter reported to the UK Health Protection Agency (HPA) [1]. A mean under-reporting factor of 7·6 has previously been recorded [2], implying that for every case reported to the HPA there are, on average, a further seven cases which go unreported. Two serotypes, Campylobacter jejuni and Campylobacter coli, are the most important in human disease and are the cause of about 90% and 10% of human cases of campylobacteriosis, respectively [3].
Poultry are considered to be an important source of Campylobacter infection; many human cases are linked to the handling and consumption of contaminated poultry meat [4, Reference Wagenaar, Nachamkin, Szymanski and Blaser5]. The Food Standards Agency (FSA) has reported that 65·2% of fresh retail chicken in the UK is contaminated with Campylobacter [3]; a Scottish study has estimated that 60–80% of human cases can be attributed to chicken meat [4]. In its current 5-year strategy for 2010–2015 the FSA has listed the reduction of Campylobacter in UK chickens as a main priority [4]. Therefore, control measures that aim to prevent or reduce the likelihood of disease being introduced to a farm are likely to have a large effect on the burden of human illness [Reference Wagenaar, Nachamkin, Szymanski and Blaser5].
Despite much research there is still considerable uncertainty in the area of Campylobacter epidemiology at the farm level, in particular the time at which birds in a flock become colonized with Campylobacter and the source(s) of infection. Many studies report that broilers become colonized after a time-lag of 2–3 weeks [3]. The presence of maternal antibodies in young chickens has been suggested as an explanation for this time-lag [Reference Cawthraw and Newell6]; however, it should be remembered that these studies are reporting detection of Campylobacter infection not the time of first infection. Studies on organic and free-range flocks have shown infection as early as 4 and 7 days, respectively [Reference Allen7] so clearly earlier infection is a possibility in some conditions. Partial depopulation (thinning) of flocks has also been shown to be a risk factor for the introduction of Campylobacter infection into a flock [Reference Lawes8], which typically occurs towards the end of a flock cycle.
The aim of this study is to estimate the time at which broiler flocks first become infected with Campylobacter by applying Bayesian methodologies incorporating within-flock transmission dynamics [Reference Hartnett9, Reference Katsma10] to longitudinal datasets on Campylobacter infection. This information is highly advantageous as it can be associated with known events in the flock cycle to give an indication as to the potential sources of the infection, e.g. thinning. In order to estimate the time at which Campylobacter is introduced into a flock the within-flock transmission dynamics of Campylobacter are mathematically described to allow determination of the prevalence of infection over time.
METHODS
Datasets
Longitudinal data on Campylobacter infection in broiler flocks were collated from a number of studies conducted in commercial UK broiler flocks [Reference Allen7, Reference Allen11–Reference Ridley13]. In each case the original authors were contacted in order that the raw data could be used in this analysis.
Flocks from study 1 [Reference Allen7] were sampled between three and seven times during their cycle, using a combination of individual caecal samples, pooled charcoal swabs and pooled faecal droppings; the number of samples taken and the time of sampling varied between farms in the study. A total of 16 flocks from study 1 were used in our analysis.
In study 2 [Reference Allen11] sampling was initiated at the feed withdrawal stage (usually between days 30 and 35) and continued at 1- to 2-day intervals until Campylobacter-positive samples were detected or the flock was cleared. On each sampling occasion 30 faecal droppings were collected from the growing house in pools of five and caecal samples were collected from 10 carcasses at the processing plant, 33 flocks from study 2 were used in our study.
In study 3 [Reference Ridley12] flocks were sampled on the day of thinning (between 33 and 36 days) by taking 30 faecal droppings (in pools of five) from the growing house and collecting 10 caecal samples from carcasses at the processing plant; a further 10 caecal samples were collected at flock clearance if Campylobacter was not detected during the first round of sampling. Our analysis included 16 flocks from study 3.
In study 4 [Reference Ridley13] flocks were sampled on three occasions during the cycle (on days ranging between 20 and 36). On each occasion 36 faecal droppings were collected in pools of six. The final sampling was timed to coincide with the flock clearance, and when practised, the second sampling took place on the day of thinning; on these occasions 16 pairs of caecal samples were collected from carcasses at the slaughter plant. A total of 53 flocks from study 4 were included in our analysis.
Our final dataset consisted of 108 flocks (94 thinned, 14 not thinned). Flock cycles were only included in the analysis if they became Campylobacter positive over the course of sampling, i.e. those flocks that remained negative until clearance or were positive at the first sampling point were removed from the analysis.
Bayesian model
The time at which a broiler flock becomes infected with Campylobacter was estimated by fitting a Bayesian model to the longitudinal dataset on Campylobacter infection; the model uses estimates of the within-flock prevalence of Campylobacter and the sensitivity of each type of sample to provide an estimate of the true prevalence at each sampling point and the estimated time of infection (t 0).
Within-flock prevalence
The model assumes that the spread of Campylobacter within a broiler flock can be described by a simple susceptible-infected (SI) model, in which birds can be in either one of two states, susceptible or infected at any time [Reference Van14], and that once infected, a bird cannot revert to susceptible status. S(t) is defined as the proportion of birds in a flock which are not infected with Campylobacter at time t, whereas I(t) is the proportion that are infected. The number of new infections caused by an infected bird each day is defined as the transmission rate parameter (β). The change in S(t) and I(t) over time can thus be written as
The within-flock prevalence at time t (p(t)) is equivalent to I(t); equations (1) and (2) can be solved analytically to give an estimate of I(t) and thus the within-flock prevalence of a flock at time t can be written as
where I(t 0) is the proportion of flock i that is Campylobacter positive at the time at which that flock first becomes infected. Infection within a flock is assumed to start with just one bird, i.e. I(t 0) = 1/N(t 0), where N(t 0) is the flock size. To facilitate the Bayesian analysis equation (3) is rearranged in the form
Equation (4) is then adjusted to consider individual flocks i (i = 1, …, 108) at sampling time j (j = 1, …, j i , where j i represents the number of times flock i was sampled). The within-flock prevalence of flock i at sampling time j therefore follows the logistic regression curve shown in equation (5)
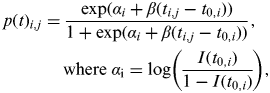 $$\eqalign{ p(t){}_{i,j} = \tab\displaystyle{{\exp (\alpha _i + \beta (t_{i,j} - t_{0,i} ))} \over {1 + \exp (\alpha _i + \beta (t_{i,j} - t_{0,i} ))}},\;\cr \tab{\rm where}\;\alpha _{\rm i} = \log \left( {\displaystyle{{I(t_{0,i} )} \over {1 - I(t_{0,i} )}}} \right),$$
$$\eqalign{ p(t){}_{i,j} = \tab\displaystyle{{\exp (\alpha _i + \beta (t_{i,j} - t_{0,i} ))} \over {1 + \exp (\alpha _i + \beta (t_{i,j} - t_{0,i} ))}},\;\cr \tab{\rm where}\;\alpha _{\rm i} = \log \left( {\displaystyle{{I(t_{0,i} )} \over {1 - I(t_{0,i} )}}} \right),$$
where t has been substituted by (t i,j – t 0,i ) to represent the time since the flock became infected; t i,j is the age of the birds in flock i at sampling time j, and t 0, the unknown parameter, is the time of infection for that flock.
Sample sensitivity
The probability of a caecal sample taken from flock i at sampling time j testing positive (p(t)ce i,j ) is given by the product of the within-flock prevalence and the sample sensitivity (as these were taken from individual birds and not pooled), i.e.
For pooled samples a different approach is required to take into account the fact that several individual birds contributed to each sample, thus increasing the likelihood of including positive birds in the sample. It was assumed that there was no reduction in the sensitivity of mixing of positive and negative samples, and therefore the probability of a positive sample for pooled charcoal and faecal samples is given as
where n is the number of samples in each particular pool.
For each sampling point in the dataset the number of samples testing positive is assumed to follow a Binomial distribution with p equal to the probability of the sample testing positive [as determined by either equations (6), (7) or (8) depending on the type of sample] and n equal to the number of samples taken on that occasion.
Analysis of results
The primary output from the model is the time at which each flock in the dataset is estimated to have become infected with Campylobacter (t 0,i ). These results therefore give some insight into when broiler flocks in the UK become infected with Campylobacter. The collated longitudinal dataset also contains other information such as the day on which infection was detected in each flock (t d,i ) and the time of thinning for each flock (t T,i ). These data can be used to calculate the difference between t 0 and infection detection (D d) and the difference between t 0 and thinning (D T) for each flock.
Such analysis can help identify any correlation between these events and potentially provide evidence for the source of Campylobacter infection in broiler flocks.
Model implementation
The model was implemented in WinBUGS version 1.4.3 and run from Matlab using matbugs, a Matlab interface for WinBUGS (www.code.google.com/p/matbugs). The model was run for a burn-in period of 1000 iterations and updated for a further 4000 iterations. Convergence was verified by running the model for three sets of different starting values and the use of the Gelman–Rubin statistic [Reference Gelman15], and also visual checking of the history plots of each parameter to check a stationary distribution had been arrived at. For each parameter in the model a prior value was assigned (either an informed prior based on data or an uninformed prior where no data are available), and the posterior values for each parameter are generated by the model and recorded for analysis. A summary of the priors for each parameter is presented in Table 1.
Table 1. A description of the model parameters and the prior distributions used for each parameter in the baseline model for estimating the time at which broiler flocks are infected with Campylobacter

n.a., Not applicable.
Estimation of prior values
The prior for the transmission rate parameter is assumed to follow a Normal distribution with a mean of 2·37 (new infections per infected bird each day) [standard deviation (s.d.) = 0·295], as estimated in a previous study of C. jejuni-colonized broiler flocks [Reference Van14].
Previous studies have indicated that flocks do not tend to become infected (or at least infection is not detected) in the first 2–3 weeks of a cycle [Reference Van14, Reference Van16]. However, given that estimating the time of infection was the main aim of our study, and the potential effect of any informative prior, the prior for t 0 was assumed to follow a Uniform distribution ranging between 0 and 50, thus encompassing all possible days of infection.
The BetaBuster software tool (University of California, Davis) was used to define Beta priors for the sensitivity of each sample type (S ce, S ch, S fe) as required in equations (6)–(8). BetaBuster is a software tool that allows specific Beta distributions to be obtained based on a best guess of the mode value and the 95% confidence interval of the desired distribution. For example, when the best guess of the sensitivity of a test is given as 0·9 and the assertion is that there is 95% certainty that the sensitivity is > 0·75, a Beta(22·99, 3·44) distribution is obtained (example taken from http://www.epi.ucdavis.edu/diagnostictests/betabuster.html).
For non-pooled caecal samples (S ce) a previous study involving the parallel sampling of flocks with boot swabs, pooled faecal samples and caecal samples, and analysis of the data using Bayesian methods, indicated that the sensitivity when testing a caecal sample from an individual bird is between 83% and 89% [Reference Vidal17]. The Beta distribution was therefore fitted assuming 95% confidence that the sensitivity was >0·83 with a mode of 0·86. This resulted in a Beta prior [Beta(a, b)] for caecal sample sensitivity with parameters a = 374·2 and b = 61·7. For pooled faecal samples a sensitivity of 0·82 (0·73, 0·89), median (2·5%, 97·5%) has been reported [Reference Vidal17], therefore for pooled samples a Beta prior with parameters a = 57·2, b = 13·3 was estimated.
Sensitivity analysis
A number of sensitivity analyses were performed to test to what extent the model results were affected by the choice of prior distributions. Parameters relating to the within-flock prevalence and the spread of Campylobacter within a flock (α and β) are some of the most important in the model and therefore the sensitivity analyses focused on these parameters. In the baseline model the transmission parameter was given a Normally distributed prior with a mean of 2·37 (infections per infected bird per day) (s.d. = 0·295) [Reference Van14]. An earlier study by the same authors gave a much lower value of 1·04 infections per day for the transmission rate [Reference Van16] and therefore an alternative Normally distributed prior with a mean of 1·04 (s.d. = 0·295) was used in the sensitivity analysis; a second analysis assigned a non-informative prior to this parameter.
Another assumption in the baseline model is that infection within a broiler flock starts with a single bird, i.e. the parameter I(t 0,i ) = 1/N(t 0,i ). However, it is possible that many birds could become infected when Campylobacter is first introduced to a flock; infection would therefore be likely to spread to a greater number of birds over the subsequent days compared to the baseline. The assumption was therefore considered in the sensitivity analysis by assigning a higher value for I(t 0,i ) corresponding to a scenario where 10 birds are infected when Campylobacter is introduced into a flock, i.e. I(t 0,i ) = 10/N(t 0,i ).
RESULTS
For each flock in the dataset a separate estimate of the time of infection is produced by the model. A histogram of the median t 0 for each flock is given in Figure 1. The peak of this histogram is between 30 and 35 days, implying that a large number of the flocks became infected between 4 and 5 weeks of age. However, the median time of infection for the flocks ranges from 10–45 days thus suggesting that the time of initial infection can vary greatly between flocks.

Fig. 1. The median estimate for the time at which each of the 108 broiler flocks in the dataset first became infected with Campylobacter (t 0).
Analysis of the posterior distributions shows that only 5·55% of results fall outside the 10–45 days range given above; the average probability across all flocks of the estimated time of infection being before day 10 is 3·28%. This rises to 8·11%, 19·31% and 30·96% for times of infection before days 20, 25 and 30, respectively.
Using additional information from the dataset it is possible to calculate the duration of time between the estimated time of infection (t 0 as given by the model) and the actual time of detection of Campylobacter in each flock, i.e. the day on which the first positive sample was recorded (D d,i ). These results suggest that Campylobacter is often introduced into a flock around a week before the infection is detected (Fig. 2), although in some cases it can be as long as 2 weeks.
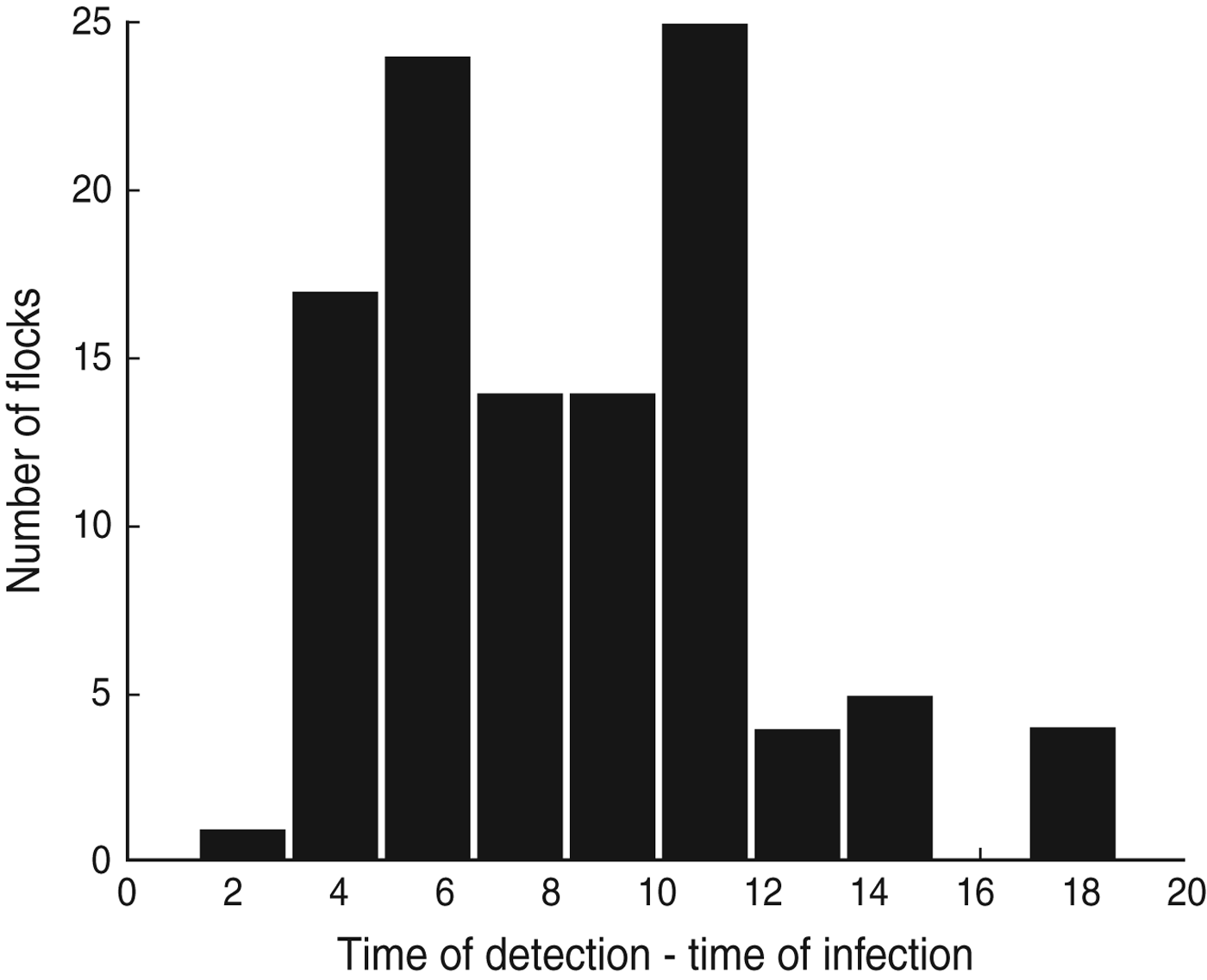
Fig. 2. The difference between the day of first observed Campylobacter detection and the median estimated day of infection for each of the 108 UK broiler flocks (D d).
Posterior estimates
The posterior estimates for each of the model parameters are given in Table 2. The posterior estimate for the transmission rate parameter (β = 1·78) is lower than the prior value (β = 2·37) implying that Campylobacter spread through the flocks contained in the dataset at a slower rate than those flocks in the study that were used to estimate the prior value [Reference Van14]. For the sensitivity of caecal samples the posterior is higher than the prior value, suggesting that this sample type may be even more sensitive than that estimated in the study from which the prior was derived [Reference Wagenaar, Nachamkin, Szymanski and Blaser5].
Table 2. The posterior parameter estimates from a Bayesian model applied to longitudinal data on Campylobacter infection in 108 UK broiler flocks in order to estimate the time at which each flock became infected with Campylobacter

For the pooled sample types the median posterior values are lower than prior value (78% and 74% compared to a median prior of 82% for charcoal and faecal samples, respectively), suggesting these sample types are not as sensitive as in the previous study [Reference Vidal17]. However, our posteriors have narrower credible intervals for the sensitivity estimates compared to the previous study, implying a greater certainty in the results.
Analysis of thinned flocks
Of the 108 flocks/cycles included in the final dataset, 94 were thinned while the remaining 14 were not. Thinning has previously been noted as a potential risk factor for the introduction of Campylobacter into broiler flocks [Reference Lawes8]. When the results from thinned flocks were separated from those that were not thinned the mean estimated time of infection for thinned flocks was day 32 while for non-thinned flocks the mean value was day 26. A hypothesis test (by use of the Deviance Information Criterion [Reference Spiegelhalter18]) showed no difference between these values; however, given the small number of non-thinned flocks in the dataset, it was considered that there was limited power to detect such a difference. We therefore looked at the relationship between the estimated time of infection and the time of thinning in the thinned flocks in order to gain more insight into the dynamics of Campylobacter infection in these flocks.
Campylobacter was detected before the day of thinning in 13 of the 94 flocks in the dataset, therefore in these flocks it is not possible that thinning was the cause for the introduction of Campylobacter. For the remaining 81 flocks the difference between the day of thinning and the median estimated day of infection, D T,i [equation (10)], was calculated to give a distribution of how close the estimated day of infection is to the day at which the flock was thinned (Fig. 3). The peak of this distribution is around 0, indicating an association between thinning and Campylobacter infection in a large number of the flocks. Of the 81 flocks where infection was not detected prior to thinning, 39 (48%) had a median estimated day of infection within 2 days of the day the flock was thinned. Analysis of the posterior distributions shows 37·9% of the predicted days of infection being within 2 days of the day of thinning, with only 17·3% of results falling after this period later in the cycle. The substantial number of flocks with a predicted time of infection close to the day in which the flock was thinned is further evidence of an association between thinning and the introduction of Campylobacter.

Fig. 3. The difference between the day on which UK broiler flocks were thinned and the median estimated day of Campylobacter infection (D T).
Sensitivity analysis
The results of these sensitivity analyses are given in Table 3. These results indicate that a change in the prior values given to the within-flock prevalence and transmission rate parameters has only a small effect on the final results; neither the posterior estimates for the time of infection nor the other parameters are substantially affected. The median time of infection is slightly later when infection is seeded with a higher number of birds, as would be expected as the time from initial infection to full prevalence would be shorter when a higher number of infected birds seed the infection. However, overall the changes observed are relatively small and therefore would not affect any conclusions derived in this analysis. Therefore the choice of priors was deemed to be appropriate.
Table 3. A summary of the results of a sensitivity analysis giving posterior parameter estimates from a Bayesian model applied to longitudinal data on Campylobacter in UK broiler flocks
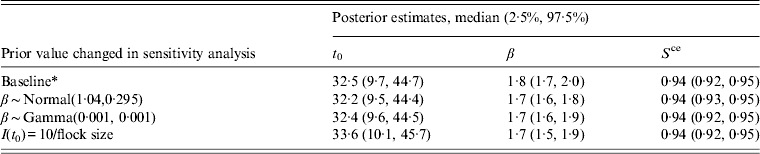
* Baseline prior values β ∼ Normal(2·37, 0·295), I(t 0) = 1/flock size.
DISCUSSION
In this study we have applied a Bayesian model to a longitudinal dataset on Campylobacter infection in broiler flocks in the UK, which has estimated that for the majority of flocks the time of initial infection is between 30 and 35 days. The thinning (partial depopulation) of a flock is an event that has previously been identified as a risk factor for the introduction of Campylobacter into a broiler flock [Reference Lawes8], possibly due to a reduction in biosecurity when catchers enter the housing to remove a proportion of the birds. The time and proportion of birds thinned will vary between flocks; however, in almost half of the thinned flocks the estimated day of infection is within 2 days of the day at which those flocks were thinned. The model results therefore suggest a link between thinning and the introduction of Campylobacter into a broiler flock.
It has also been suggested that a change in feed may be an important risk factor for Campylobacter introduction due to changes in the gut of the birds [19] making the birds more susceptible to infection. While the exact time of feed change varies between production companies there is often a change around 10 days and again around 30 days (R. Davies, AHVLA, personal communication). It is possible that the large number of results between 30 and 35 days is an indication that feed change is a contributor to the introduction or spread of Campylobacter within broiler flocks. However, given that there is no specific longitudinal data considering the timing of feed changes and that the time of feed change is similar to the time of thinning it is hard to discriminate between the two potential risk factors and therefore not possible to conclude with any certainty that feed change is a contributor to the initiation of Campylobacter infection.
The model results suggest that infection often occurs at least a week before it could be detected. This may be because the prevalence during early stages of flock infection is too low to be detected by the sampling methods. Additionally, the frequency of sampling within a particular study will have a significant effect on the duration of time between infection and detection of a Campylobacter-positive sample. The within-flock prevalence for a hypothetical flock of 28 500 birds (about the average flock size in the dataset) after seeding of infection with a single bird at day 0 is shown in Figure 4; this shows that infection can spread to 95% prevalence in a flock within ∼8 days of the initial infection (β = 1·78). In some of the flocks used in the dataset there were intervals between samples of >10 days. Given that infection can spread to almost 100% of the flock in 8 days it is possible that intervals of this length between samples could provide little or no longitudinal data on the change in Campylobacter prevalence over time. In those flocks where the interval between samples was very long there is therefore more uncertainty associated with the estimated time of infection; however, more accurate results cannot be achieved without better input data for the model. It is therefore recommended that in future studies sampling should occur at intervals of ⩽1 week, with perhaps more frequent sampling once the birds have reached age 3 weeks, as the results suggest that most flocks may not be infected until after this point. Following these sampling recommendations would provide the best data for Bayesian models such as the one developed in this study.
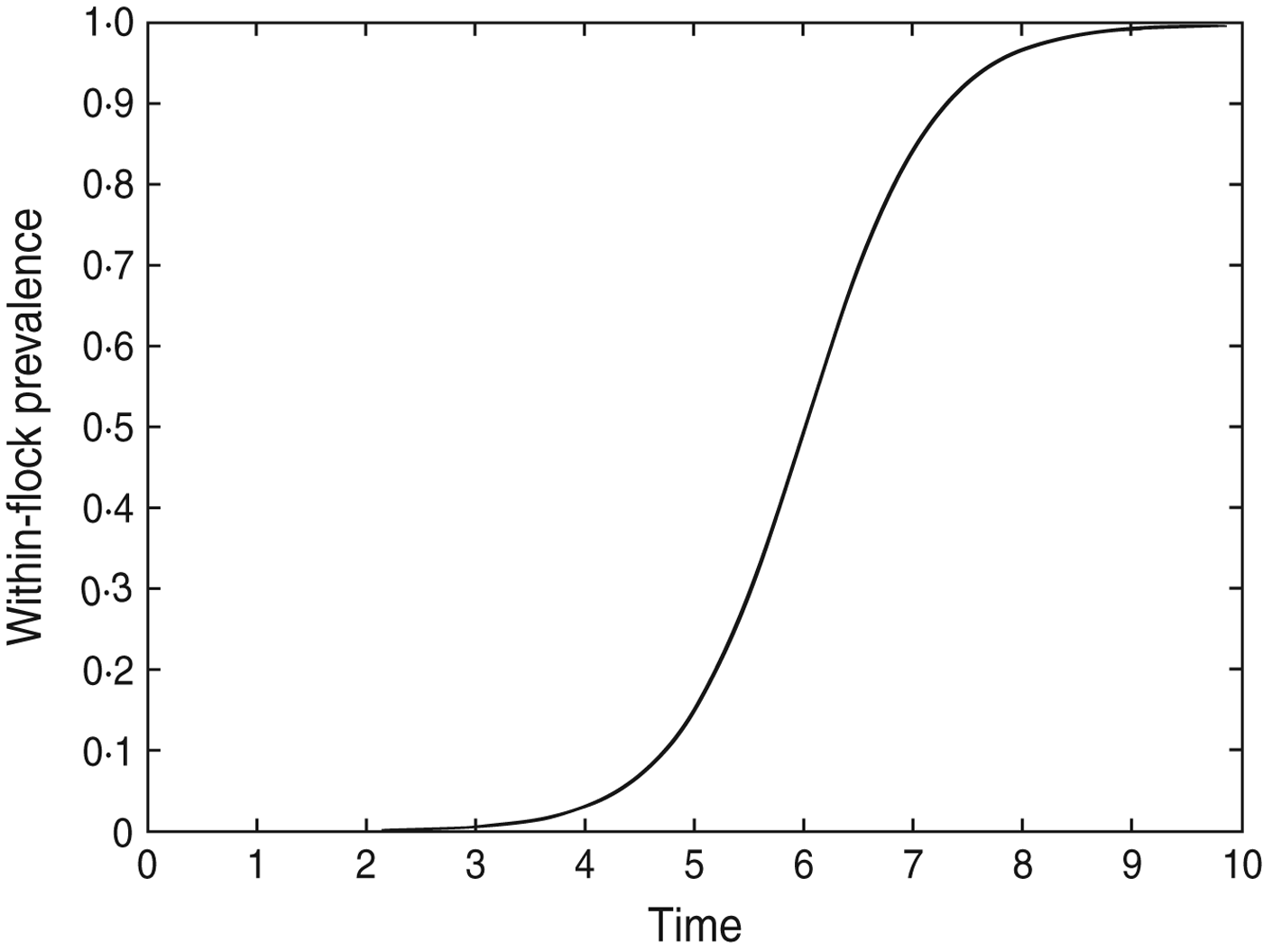
Fig. 4. The within-flock prevalence curve for a 28 500 bird flock in which Campylobacter infection is initiated on day 0 by a single bird, β = 1·78.
The transmission rate of Campylobacter within a flock is an important parameter in the model; the median value for the posterior estimate of this parameter is 1·78, i.e. each infected bird causes about 1·8 secondary infections per day. This parameter is lower than the assigned prior value of 2·37 estimated from a 2009 study [Reference Van14], but higher than the value of 1·04 given by the same authors in an earlier paper [Reference Van16]. In the earlier study, broiler flocks were inoculated with various Campylobacter strains [Reference Van16] whereas the later study used longitudinal datasets collected in Queensland, Australia [Reference Van14]. Different strains of Campylobacter are likely to spread throughout flocks at different rates and therefore the posterior estimates of the transmission rate given here represent the average transmission rate across all of the flocks in the UK dataset. In individual flocks, Campylobacter may be expected to spread between birds at a faster or slower rate depending on the environment the flock is kept in and the transmission ability of the particular strain or strains of Campylobacter causing the infection.
In this study, the time at which a flock becomes infected with Campylobacter has been estimated to range between 10 and 45 days, with a most likely value around 30–35 days. These results are consistent with a previous study on the transmission of Campylobacter within commercial broiler flocks which concluded that flocks become infected after day 21 [Reference Van14]; the most common day of infection in that particular study was around day 30. In a previous AHVLA maximum-likelihood model, the day of infection was estimated to range between 18 and 48 days [Reference Snary, Kosmider and Haq20], again a similar range of results to those estimated here; however, only two of the 13 thinned flocks analysed showed a strong link between thinning and Campylobacter infection. The results of the current analysis suggest a stronger association between the time at which a flock is thinned and the time that flock becomes infected with Campylobacter.
The Bayesian methodologies used in this analysis utilize longitudinal data on Campylobacter infection in broiler flocks; these methods rely on flocks becoming positive over the sampling period and provide the most accurate results when multiple samples are taken over many time periods. In the raw data taken from the previous studies a number of flocks were only sampled on one occasion and thus could not be used in the analysis. Other flocks were Campylobacter positive on the first day of sampling and could therefore also not be used. The removal of these Campylobacter-positive flock cycles from the analysis potentially adds bias to the results as these flocks are likely to have an earlier time of first infection than those which were negative at the first sampling point. One study in particular took samples on very few occasions, a number of which were positive at the first sampling point [Reference Ridley13] and could not be used. The remaining flocks from this study could therefore be skewing the results. This potential bias was considered by removing that study from the dataset and re-running the model (results not shown). This removal of this data did not significantly alter the outputs, and would not have affected any conclusions made in this study. Thus it can be concluded that the inclusion of this study in the model is not introducing a significant bias to the results.
To the authors' knowledge this study represents the first time that Bayesian methodologies have been applied to a large dataset compiled from commercial UK broiler flocks to estimate the time at which Campylobacter was first introduced into these flocks. This work extends previously used methods [Reference Van14, Reference Van16] by considering multiple sample types at each time of sampling and comparing the model results with on-farm risk factors for Campylobacter, such as thinning and feed changes. These results give insights into potential sources of infection and can also be used in on-farm transmission models and Campylobacter risk assessments. These methods could easily be applied to other zoonoses or livestock systems with similar disease dynamics and management structures by changing the zoonoses/species dependent parameter values such as the transmission rate and test sensitivities.
ACKNOWLEDGEMENTS
This work was funded by the UK Department for Environment, Food and Rural Affairs (Defra) under project OZ0619. The authors thank the UK Food Standards Agency for granting permission to use the B15004 and B15020 longitudinal datasets within this project. In addition, we acknowledge Joanna Lawes of the Animal Health and Veterinary Laboratories Agency (AHVLA) for providing expertise in Campylobacter epidemiology, Dr Neil Donaldson (formerly of the AHVLA) for helping to collate the data for use in the model and Dr Louise Kelly (AHVLA/University of Strathclyde) for providing a mathematical review of the techniques used in this study.
DECLARATION OF INTEREST
None.








