Impact Statement
Snow on sea ice is a critical component of the earth system; however, its current representation in climate models is limited because of the high computational needs of models like SnowModel. This work introduces a data-driven approach to emulate SnowModel while following the underlying physics of the snowpack evolution.
1. Introduction
Snow is a critical component of the Arctic sea ice system, with unique thermal and optical properties that control sea ice thermodynamics. Snow has low thermal conductivity values that hinder sea ice growth in winter (Sturm et al., Reference Sturm, Perovich and Holmgren2002; Macfarlane et al., Reference Macfarlane, Löwe, Gimenes, Wagner, Dadic, Ottersberg, Hämmerle and Schneebeli2023), and high albedo that delays the sea ice from melting in summer. Both the thermal and optical properties of snow are affected by the state of the snowpack, i.e., the snow depth, density, and the snow grain size and type of different snow layers. Information on the spatial distribution and temporal evolution of the snowpack states is important for both process modeling and remote sensing applications. A big challenge associated with scaling is that snowpack states demonstrate large spatial variations at scales of a few meters that are beyond the coarse spatial resolution of both satellite observations and large-scale sea ice models.
SnowModel is a numerical process model that simulates the evolution and spatial distribution of snow physical properties and structural characteristics in a multilayer snowpack framework (Liston and Elder, Reference Liston and Elder2006). It is applicable to any environment experiencing snow, including sea ice applications (Liston et al., Reference Liston, Polashenski, Rösel, Itkin, King, Merkouriadi and Haapala2018). SnowModel is a collection of modeling tools designed to be versatile in terms of spatial domain (from regional to global applications), temporal domain (for past, current, and future climates), spatial resolution (e.g., 1 m to 100 km), and temporal resolution (e.g. 1 hour to daily). Meteorological information is required as an input to drive the SnowModel. It specifically requires meteorological station, or atmospheric datasets, that include air temperature, relative humidity, precipitation, wind speed, and wind direction. Topography information is also required for simulating snow distributions because in SnowModel snow is blown and redistributed by the wind, accumulating in the lee side of wind obstruction features.
A significant limitation of physical numerical models, like SnowModel, lies in their high computational requirements, which makes them less feasible for some practical applications due to the high resources required. SnowModel specifically is written in Fortran 77 and has no model components that can be run in parallel, making its performance even slower. On the other hand, machine learning (ML) has shown potential in enhancing climate models, particularly in replacing or supplementing components of traditional models. This is evident in applications such as simulating cloud convection using random forests and deep learning models (Beucler et al., Reference Beucler, Ebert-Uphoff, Rasp, Pritchard and Gentine2023) and in emulating ocean general circulation models through neural networks (Agarwal et al., Reference Agarwal, Kondrashov, Dueben, Ryzhov and Berloff2021). In the cryosphere, recent developments include the creation of emulators for Ice Sheet Models to project sea level rise using Gaussian processes (Berdahl et al., Reference Berdahl, Leguy, Lipscomb and Urban2021) and long short-term memory (LSTM) networks (Van Katwyk et al., Reference Van Katwyk, Fox-Kemper, Seroussi, Nowicki and Bergen2023).
Despite the progress made with ML, data-driven emulators face their own set of challenges. First, there is the concern of generalizability: these models often struggle to extend their applicability beyond the conditions and data they were trained on Jebeile et al. (Reference Jebeile, Lam, Majszak and Räz2023). Second, the opacity of ML models poses a significant issue. Often referred to as “black box” models, they lack transparency, offering little to no insight into the reasoning behind their predictions (McGovern et al., Reference McGovern, Ebert-Uphoff, Gagne and Bostrom2022). Third, a critical limitation is their inability to adhere to fundamental physical laws, including the conservation of mass, which is an important principle in process-guided models (Kashinath et al., Reference Kashinath, Mustafa, Albert, Wu, Jiang, Esmaeilzadeh, Azizzadenesheli, Wang, Chattopadhyay and Singh2021; Sudakow et al., Reference Sudakow, Pokojovy and Lyakhov2022). To tackle these challenges, physics-guided ML has recently emerged as a promising approach. This involves incorporating physical laws within the ML framework. It can be achieved by softly constraining the loss function of the model, thereby guiding it to make predictions that are not only accurate but also consistent with physical principles (Kashinath et al., Reference Kashinath, Mustafa, Albert, Wu, Jiang, Esmaeilzadeh, Azizzadenesheli, Wang, Chattopadhyay and Singh2021). In broader climate science, recent studies have demonstrated that physics-guided ML models exhibit robustness and have a higher adherence to physical principles. Additionally, these models demonstrate increased data efficiency, requiring fewer data points for training compared to traditional ML models that do not incorporate physical constraints (Kashinath et al., Reference Kashinath, Mustafa, Albert, Wu, Jiang, Esmaeilzadeh, Azizzadenesheli, Wang, Chattopadhyay and Singh2021; Beucler et al., Reference Beucler, Pritchard, Rasp, Ott, Baldi and Gentine2021). In our work, we develop and evaluate ML-based emulators of SnowModel for modeling snow on sea ice. Our key contributions are as follows:
-
• We develop and compare ML architectures for predicting the density of snow on sea ice.
-
• We explore the use of physics-guided loss functions to constrain the emulator using the underlying physics of snowpack formation.
2. Methods
2.1. Study region and dataset construction
We utilized the SnowModel to generate a comprehensive dataset covering the snow dynamics in various regions in the Arctic. Due to the lack of availability of high-resolution sea-ice topography data, we synthetically created ice topographic features in these regions by generating random sea-ice ridges based on the minimum, maximum, and standard deviation of the sea ice ridges described in Sudom et al. (Reference Sudom, Timco, Sand and Fransson2011). The dataset for the emulator was created by running the SnowModel across five distinct Arctic regions (Figure 1) over 10 years. The selected regions spanned over different Arctic Seas that are influenced by a wide range of atmospheric conditions (Central Arctic, Beaufort, Chuckhi, Laptev, and Barents Seas), resulting in a broad variety of snowpack characteristics.

Figure 1. Arctic study regions.
2.2. SnowModel configuration
We used NASA’s Modern Era Retrospective Analysis for Research and Application Version 2 (MERRA-2; Global Modeling and Assimilation Office (GMAO), 2015) as meteorological forcing to SnowModel. Specifically, SnowModel was forced with 10-m wind speed and direction, 2-m air temperature and relative humidity, and total water-equivalent precipitation from MERRA-2 (Table 1). The simulations began in August 2010 and ran through August 2020. Temporal resolution was 3 hours to capture diurnal variations of the snow properties. The outputs were saved daily at the end of each day.
Table 1. Variables driving SnowModel and inputs for emulators

2.3. LSTM architecture
LSTM networks are a special class of recurrent neural networks (RNNs) that are designed to address the challenge of learning long-term dependencies in sequential data (Hochreiter and Schmidhuber, Reference Hochreiter and Schmidhuber1997). Traditional RNNs often struggle with the vanishing or exploding gradient problem, which hampers their ability to retain information over extended sequences (Bengio et al., Reference Bengio, Simard and Frasconi1994). LSTMs mitigate this issue through a unique architecture consisting of memory cells and multiple gates. Each LSTM unit contains three gates: input, forget, and output. The input gate controls the influx of new information into the cell state, the forget gate manages the retention or removal of information, and the output gate influences the contribution of the cell state to the output. This gating mechanism is used for preserving information across long sequences, allowing LSTMs to effectively learn tasks involving sequential data, such as time-series data. In our model, the input layer accommodates the five primary features. This is followed by two LSTM layers with 128 units each, for capturing the sequential patterns in the data. Dropout layers, set at a rate of 0.25, are used after each LSTM layer to prevent overfitting. A dense layer with 64 units featuring a ReLU activation function is integrated, succeeded by a dropout layer at a rate of 0.25. The final output layer is structured to predict snow density and two additional variables, snow depth and snow temperature. We use these additional variables while constructing the physics-constrained loss function for the LSTM. The models were implemented in Python using PyTorch (Paszke et al., Reference Paszke, Gross, Massa, Lerer, Bradbury, Chanan, Killeen, Lin, Gimelshein and Antiga2019).
2.4. Physics-guided LSTM
We developed a loss function to incorporate the physics of snowpack formation in the LSTM model. As snow accumulates, the lower layers of the snowpack are subjected to increasing pressure due to the weight of the snow above. This pressure causes the snow grains in the lower layers to compact or press closer together. As a result, the density of the snow in these lower layers increases. This process of density increase due to compaction is included in SnowModel’s SnowPack component and it provides key equations explaining the snow compaction dynamics (Liston and Elder, Reference Liston and Elder2006). The equation for density increase due to compaction is given by
 $$ \frac{\partial {\rho}_s}{\partial t}={A}_1\cdot {h}_w^{\ast}\cdot \frac{\rho_s\exp \left(-B\left({T}_f-{T}_s\right)\right)}{\exp \left(-{A}_2{\rho}_s\right)} $$
$$ \frac{\partial {\rho}_s}{\partial t}={A}_1\cdot {h}_w^{\ast}\cdot \frac{\rho_s\exp \left(-B\left({T}_f-{T}_s\right)\right)}{\exp \left(-{A}_2{\rho}_s\right)} $$
where
![]() $ {\rho}_s $
is the snow density (kg/m3),
$ {\rho}_s $
is the snow density (kg/m3),
![]() $ t $
represents time (s),
$ t $
represents time (s),
![]() $ {h}_w^{\ast }=\frac{1}{2}{h}_w $
is the weight of snow defined as half of the snow water equivalent
$ {h}_w^{\ast }=\frac{1}{2}{h}_w $
is the weight of snow defined as half of the snow water equivalent
![]() $ {h}_w $
,
$ {h}_w $
,
![]() $ {T}_f $
is the freezing temperature of water (K), and
$ {T}_f $
is the freezing temperature of water (K), and
![]() $ {T}_s $
is the average snow-ground interface and surface temperatures (K). Constants
$ {T}_s $
is the average snow-ground interface and surface temperatures (K). Constants
![]() $ {A}_1 $
,
$ {A}_1 $
,
![]() $ {A}_2 $
, and
$ {A}_2 $
, and
![]() $ B $
are derived from empirical studies:
$ B $
are derived from empirical studies:
![]() $ {A}_1=0.0013 $
m−1 s−1,
$ {A}_1=0.0013 $
m−1 s−1,
![]() $ {A}_2=0.021 $
m3 kg−1, and
$ {A}_2=0.021 $
m3 kg−1, and
![]() $ B=0.08 $
K−1.
$ B=0.08 $
K−1.
The snow water equivalent,
![]() $ {h}_w $
(m), is defined as
$ {h}_w $
(m), is defined as
Here,
![]() $ {\rho}_w $
is the density of water (kg/m3), and
$ {\rho}_w $
is the density of water (kg/m3), and
![]() $ {\zeta}_s $
is the snow depth (m).
$ {\zeta}_s $
is the snow depth (m).
In other words,
 $$ {\rho}_{s,\mathrm{phys}}\left(t+\Delta t\right)={\rho}_{s,\mathrm{phys}}(t)+0.5\cdot \Delta t\cdot {A}_1\cdot \frac{\rho_{s,\mathrm{pred}}(t)}{\rho_w}\cdot {\zeta}_{s,\mathrm{pred}}(t)\cdot \frac{\rho_{s,\mathrm{pred}}(t)\exp \left(-B\left({T}_f-{T}_{s,\mathrm{pred}}(t)\right)\right)}{\exp \left(-{A}_2{\rho}_{s,\mathrm{pred}}(t)\right)} $$
$$ {\rho}_{s,\mathrm{phys}}\left(t+\Delta t\right)={\rho}_{s,\mathrm{phys}}(t)+0.5\cdot \Delta t\cdot {A}_1\cdot \frac{\rho_{s,\mathrm{pred}}(t)}{\rho_w}\cdot {\zeta}_{s,\mathrm{pred}}(t)\cdot \frac{\rho_{s,\mathrm{pred}}(t)\exp \left(-B\left({T}_f-{T}_{s,\mathrm{pred}}(t)\right)\right)}{\exp \left(-{A}_2{\rho}_{s,\mathrm{pred}}(t)\right)} $$
To align the LSTM model’s predictions with these physical principles, we constructed a physics-informed loss function,
![]() $ {L}_{\mathrm{physics}} $
. This loss function consists of the mean squared errors (MSE) between the model’s predicted values for snow density, depth, and temperature, and their corresponding values from the SnowPack equations.
$ {L}_{\mathrm{physics}} $
. This loss function consists of the mean squared errors (MSE) between the model’s predicted values for snow density, depth, and temperature, and their corresponding values from the SnowPack equations.
The combined loss function is therefore expressed as
where
![]() $ {L}_{\mathrm{LSTM}} $
represents the initial loss from the LSTM model predictions, and
$ {L}_{\mathrm{LSTM}} $
represents the initial loss from the LSTM model predictions, and
![]() $ \lambda $
is a regularization parameter that balances the contribution of the physics-informed loss in the overall objective function. This objective function was then used in the LSTM architecture described in Section 2.3.
$ \lambda $
is a regularization parameter that balances the contribution of the physics-informed loss in the overall objective function. This objective function was then used in the LSTM architecture described in Section 2.3.
2.4.1. Training details
In both the LSTM architectures, we used Adam optimizer, with a learning rate of 0.001, for training the models for 150 epochs with a batch size of 32. We used an early stopping mechanism, considering the validation loss after 10 epochs, to prevent overfitting. We selected model hyperparameters (number of layers, dropout, batch size, and epochs) by random search with 5-fold cross-validation. We gave the random search a budget of 50 iterations for each model.
2.5. Random forest
We chose Random Forest to compare our LSTM-based emulators. Random Forest (Breiman, Reference Breiman2001) is an ensemble learning method used for classification and regression. It operates by constructing multiple decision trees at training time and outputting the class, that is, the mode of the classes (classification) or mean prediction (regression) of the individual trees. This method is effective for prediction tasks because it reduces the risk of overfitting by averaging multiple trees, thus improving the model’s generalizability. We used Random Forest to predict snow density. The Random Forest model was configured with 500 trees.
3. Results
3.1. Predictive performance
For training and testing our emulator models, we used a cross-validation approach, specifically opting for a leave-one-out cross-validation (LOOCV) method. In this method, data from four out of five Arctic regions were used for training, while the remaining fifth region’s data served for testing purposes. This process was systematically rotated, ensuring each region was used as a test set in turn, thus providing a comprehensive assessment of the models across varied Arctic conditions. We chose the LOOCV approach as opposed to a time-based split because the distinct climatic and geographical characteristics of each Arctic region can significantly influence the model’s performance. A time-based split would not adequately capture these spatial variabilities and could lead to models that are well-tuned for temporal patterns but less robust to spatial differences. LOOCV ensures that each model is tested against the unique conditions of an unseen region, enhancing our ability to generalize our findings across the different regions, despite the diverse environmental conditions present within each region.
While evaluating the models, we also calculated the daily climatology of snow density in every region. This climatology served as a baseline for us to compare and contrast the emulator models’ predictions with a standard reference point that reflects typical conditions.
For assessing the predictive performance of our emulators (Table 2), we consider the Root mean squared error (RMSE). RMSE provides a measure of the average magnitude of the models’ prediction errors, and it is defined as
 $$ \mathrm{RMSE}=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2} $$
$$ \mathrm{RMSE}=\sqrt{\frac{1}{n}\sum \limits_{i=1}^n{\left({y}_i-{\hat{y}}_i\right)}^2} $$
where
![]() $ {y}_i $
is the observed value,
$ {y}_i $
is the observed value,
![]() $ {\hat{y}}_i $
is the predicted value, and
$ {\hat{y}}_i $
is the predicted value, and
![]() $ n $
is the number of observations.
$ n $
is the number of observations.
Table 2. Comparison of RMSE across the study regions for different emulator models. Lower values are better

The results showed that all of the model’s predictions closely matched the SnowModel outputs in all regions. All of the emulators performed better than the climatological baseline. Figures 2 and 3 show a comparison of the Snow Density as predicted by the SnowModel and physics-guided LSTM for Region 2. During this evaluation, the emulator was trained with data from Regions 1, 3, 4 and 5, and Region 2 was the test site. The emulator’s prediction aligns closely with the SnowModel which shows that the emulator can generalize to regions where it has not been trained before. The LSTM with the physics-guided Loss function performed better than the LSTM with only MSE loss in four out of five regions. The overall better performance of the PG-LSTM across the other Arctic regions suggests that incorporating physical constraints through the physics-guided loss function was generally beneficial. However, every region has its own unique characteristics in terms of meteorology, topography, and snowpack evolution dynamics. In Region 4, there may have been some conditions or processes that deviated from the assumptions made by the physics constraints used to guide the LSTM model. On the other hand, the Random Forest, being an ensemble of decision trees, has a more flexible model structure allowing to better perform in that region without being bound by explicit physical constraints.
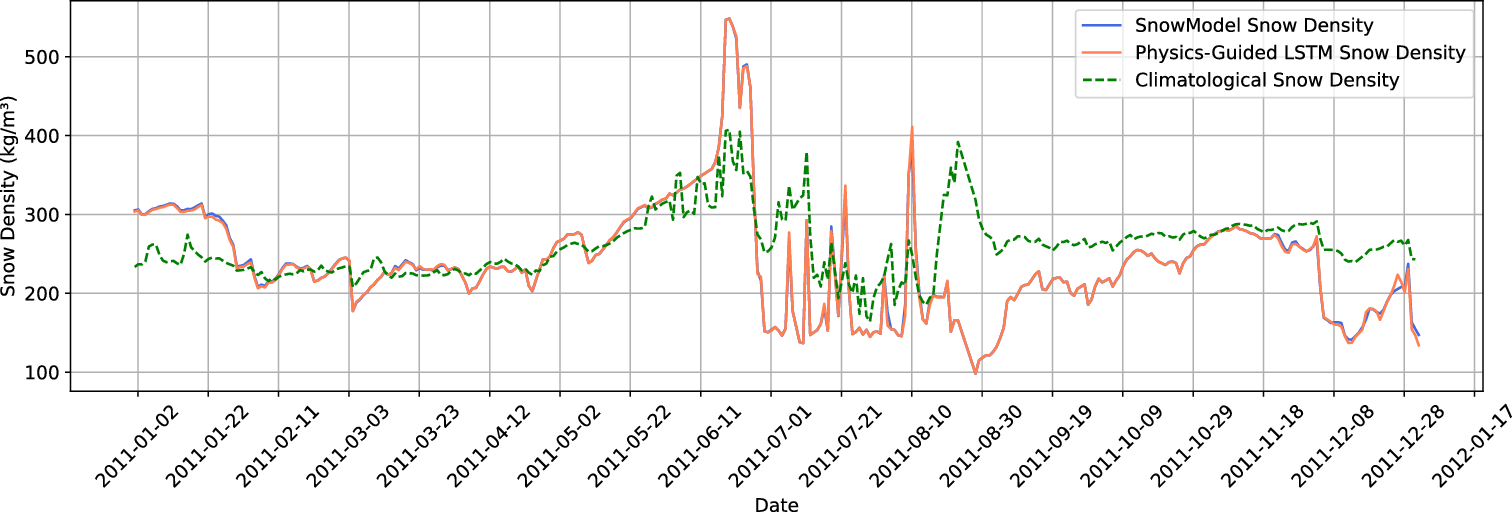
Figure 2. Predicted average snow density across all the points in Region 3 by emulator compared with the snow density from SnowModel.

Figure 3. Spatial maps showing snow density as predicted by the emulator and compared with those from the SnowModel for Region 2. The third column shows the error percentage (lower values are better), highlighting the differences between the SnowModel and the emulator.
3.2. Runtime
We conducted a runtime analysis (Table 3) by comparing the Python runtime for all of the emulators with the Fortran runtime of the original SnowModel. The runtime measurements were conducted on a high-performance computing system with NVIDIA Volta V100 GPU and Xeon Gold 6230 CPUs with 2 × 20 cores operating at 2.1 GHz. The LSTM-based models took 8 hours to train. We measured the time required to process the data for one region of resolution 1500 × 1500 in the SnowModel. As shown in Table 3, the speed-up achieved by the ML models is significant. The Random Forest, LSTM, and physics-guided LSTM models demonstrated speed-ups of 2400, 13,714, and 9931 times, respectively, compared to the SnowModel.
Table 3. Comparison of runtime between SnowModel and emulators. Lower values are better

4. Feature importances
To identify the most influential variables in estimating snow density within the physics-guided LSTM model, we used permutation importance. This method involved systematically shuffling the values of each feature within the dataset for each specific Arctic site independently. We repeated this shuffling process multiple for 10 iterations to ensure reliability and measured the effect on the model’s accuracy by observing the increase in the RMSE. This increase in RMSE, plotted on the y-axis in Figure 4, quantitatively represents the impact of each feature’s disruption on model performance. We found that air temperature and the day of the year were critical for capturing the seasonal variations in snow density, reflecting their direct influence on thermodynamics. Similarly, topography significantly affected spatial variations, influencing patterns of snow accumulation and melting due to its role in redistributing snow across the landscape. These features align with the dynamic processes in SnowModel, where snow density evolves under the influence of overlying snow weight (compaction), wind speed, sublimation of non-blowing snow, and melting processes.
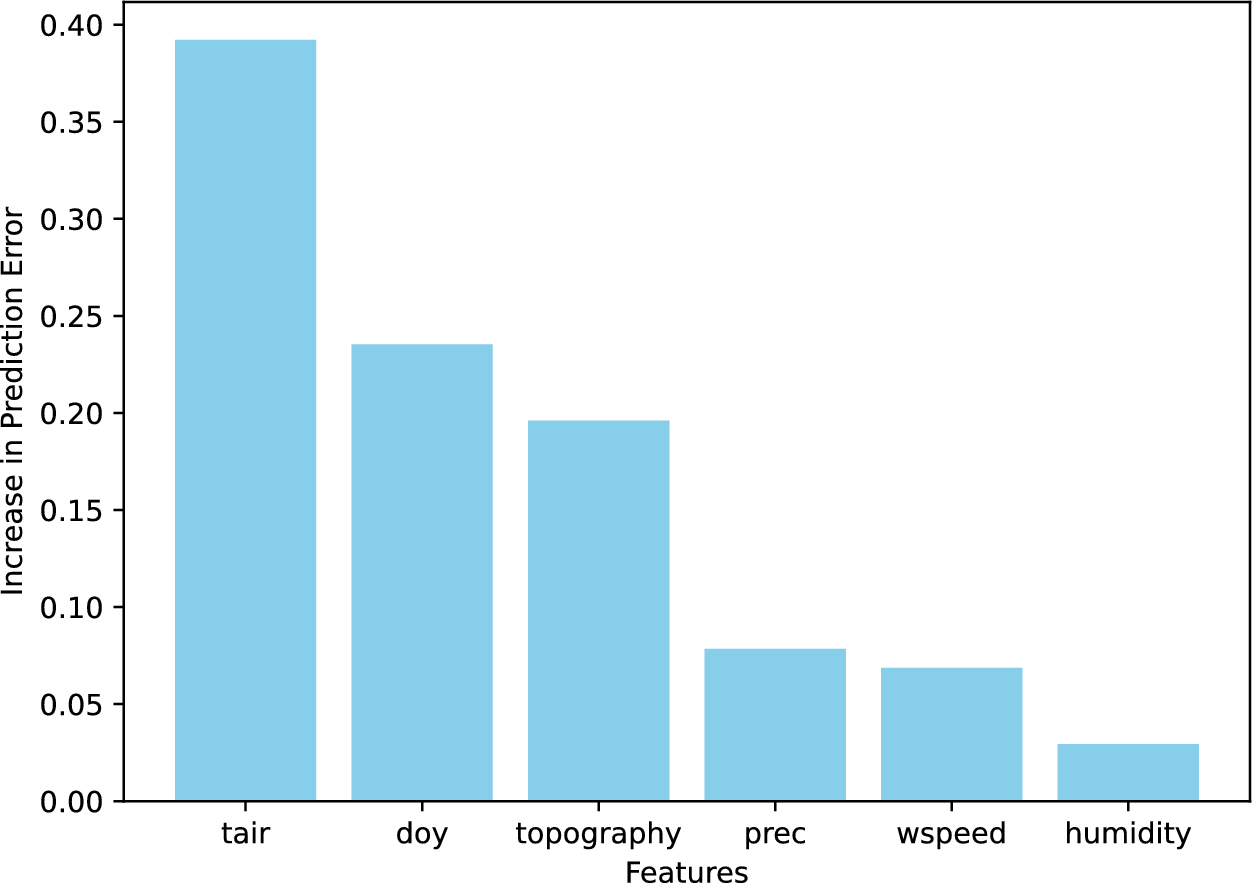
Figure 4. Feature importance derived from permutation shuffling in the physics-guided LSTM.
5. Conclusion
In this work, we explored the use of ML to emulate SnowModel. We developed and assessed various ML frameworks—Random Forest, LSTM, and physics-guided LSTM—to effectively emulate the SnowModel. The physics-guided LSTM model, in particular, showed significant improvement in prediction accuracy, as indicated by a lower RMSE. Moreover, it demonstrated a notable increase in computational speed, operating approximately 9000 times faster than SnowModel. It is worth noting that while the LSTM model benefited from incorporating the physics of snowpack formation, due to the nature of these “soft” regularizations, the constraints are not required to be strictly satisfied during runtime. In our study, we focused on emulating snow density; a similar approach could be used for emulating other variables like snow depth in SnowModel.
A potential direction for future research could be the integration of the emulator within a climate model to improve simulations of snow on sea ice, which are currently limited by the computational demands of numerical models like SnowModel. Additionally, the emulator itself could be developed further by exploring recent ML architectures like Fourier Neural Operators, which are capable of operating at arbitrary resolutions without requiring resolution-specific training. Enhancing the interpretability of these models could also be a valuable direction to ensure a clearer understanding of the model predictions and their alignment with physical processes.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/eds.2024.40.
Acknowledgments
The authors wish to acknowledge CSC—IT Center for Science, Finland, for computational resources.
Author contribution
Conceptualization: A.P., I.M., A.N.; Methodology: A.P., I.M.; Data visualization: A.P.; Writing original draft: A.P., I.M., A.N. All authors approved the final submitted manuscript.
Competing interest
None.
Data availability statement
Data used in this study is available at https://zenodo.org/records/12794391.
Ethical standard
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by the Research Council of Finland grant 341550.










Comments
Dear Environmental Data Science editors,
This is our manuscript which was accepted and presented at Climate Informatics 2024 and accepted for publication in Environmental Data Science. In this work, we develop a Physics-guided Machine learning model to emulate SnowModel in the Arctic.