Impact Statement
Weather and climate predictions are relied on by users from industry, charities, governments, and the general public. The largest source of uncertainty in these predictions arises from approximations made when building the computer model used to make them. In particular, the representation of small-scale processes such as clouds and thunderstorms is a large source of uncertainty because of their complexity and their unpredictability. Machine learning (ML) approaches, trained to mimic high-quality datasets, present an unparalleled opportunity to improve the representation of these small-scale processes in models. However, it is important to account for the unpredictability of these processes while doing so. In this article, we demonstrate the untapped potential of such probabilistic ML approaches for improving weather and climate prediction.
1. Introduction
Weather and climate models exhibit long-standing biases in mean state, modes of variability, and the representation of extremes. These biases hinder progress across the World Climate Research Programme grand challenges. Understanding and reducing these biases is a key focus for the research community.
At the heart of weather and climate models are the physical equations of motion, which describe the atmosphere and ocean systems. To predict the evolution of the climate system, these equations are discretized in space and time. The resolution ranges from order 100 km and 30–60 minutes in a typical climate model, through 10 km and 5–10 minutes in global numerical weather prediction (NWP) models, to one km and a few tens of seconds for state-of-the-art convection-permitting runs. The impact of unresolved scales of motion on the resolved scales is represented in models through parametrisation schemes (Christensen and Zanna, Reference Christensen and Zanna2022). Many of the biases in weather and climate models stem from the assumptions and approximations made during this parametrization process (Hyder et al., Reference Hyder, Edwards, Allan, Hewitt, Bracegirdle, Gregory, Wood, Meijers, Mulcahy, Field, Furtado, Bodas-Salcedo, Williams, Copsey, Josey, Liu, Roberts, Sanchez, Ridley, Thorpe, Hardiman, Mayer, Berry and Belcher2018). Furthermore, despite their approximate nature, conventional parametrization schemes account for twice as much compute time as the dynamical core in a typical atmospheric model (Wedi et al., Reference Wedi, Hamrud and Mozdzynski2013).
Replacing existing parametrization schemes with statistical models trained using ML has great potential to improve weather and climate models both in terms of reduced computational cost and increased accuracy. For example, ML has been used to emulate existing parametrization schemes, including radiation (Chevallier et al., Reference Chevallier, Cheruy, Scott and Chedin1998; Krasnopolsky et al., Reference Krasnopolsky, Fox-Rabinovitz and Chalikov2005; Ukkonen et al., Reference Ukkonen, Pincus, Hogan, Nielsen and Kaas2020) and convection (O’Gorman and Dwyer, Reference O’Gorman and Dwyer2018), realizing speed-ups of up to 80 times in the case of radiation. By emulating more complex (and therefore expensive) versions of a parametrization scheme, the accuracy of the weather or climate model can also be improved compared to the control simulation at minimal computational cost (Chantry et al., Reference Chantry, Hatfield, Dueben, Polichtchouk and Palmer2021; Gettelman et al., Reference Gettelman, Gagne, Chen, Christensen, Lebo, Morrison and Gantos2021). The accuracy of the climate model can be further improved by training ML models on high-fidelity data sets. For example, several authors have coarse grained high-resolution models which explicitly resolve deep convection to provide training data for ML models, leading to improved parametrizations (Gentine et al., Reference Gentine, Pritchard, Rasp, Reinaudi and Yacalis2018; Brenowitz et al., Reference Brenowitz, Beucler, Pritchard and Bretherton2020). Recent research has focused on challenges, including online stability (Brenowitz and Bretherton, Reference Brenowitz and Bretherton2018; Brenowitz et al., Reference Brenowitz, Beucler, Pritchard and Bretherton2020; Yuval and O’Gorman, Reference Yuval and O’Gorman2020; Yuval et al., Reference Yuval, O’Gorman and Hill2021), conservation properties (Beucler et al., Reference Beucler, Pritchard, Rasp, Ott, Baldi and Gentine2021), and the ability of ML emulators to generalize and perform well in climate change scenarios (Beucler et al., Reference Beucler, Pritchard, Rasp, Ott, Baldi and Gentine2021).
The schemes referenced above all implicitly assume that the grid-scale variables of state fully determine the parametrized impact of the subgrid scales (Palmer, Reference Palmer2019). This assumption is flawed. An alternative approach is stochastic parametrisation (Leutbecher et al., Reference Leutbecher, Lock, Ollinaho, Lang, Balsamo, Bechtold, Bonavita, Christensen, Diamantakis and Dutra2017), where the subgrid tendency is drawn from a probability distribution conditioned on the resolved scale state. Stochastic parametrization schemes are widely used in the weather and subseasonal-to-seasonal forecasting communities, where they have been shown to improve the reliability of forecasts (Leutbecher et al., Reference Leutbecher, Lock, Ollinaho, Lang, Balsamo, Bechtold, Bonavita, Christensen, Diamantakis and Dutra2017). Furthermore, the inclusion of stochastic parametrizations from the weather forecasting community into climate models has led to dramatic improvements in long-standing biases (Berner et al., Reference Berner, Achatz, Batte, De La Cámara, Christensen, Colangeli, Coleman, Crommelin, Dolaptchiev and Franzke2017; Christensen et al., Reference Christensen, Berner, Coleman and Palmer2017). While rigorous theoretical ideas exist to demonstrate the need for stochasticity in fluid dynamical models (Gottwald et al., Reference Gottwald, Crommelin, Franzke, CLE and O’Kane2017), the approaches currently used tend to be pragmatic and ad hoc in their formulation (Berner et al., Reference Berner, Achatz, Batte, De La Cámara, Christensen, Colangeli, Coleman, Crommelin, Dolaptchiev and Franzke2017). There is therefore great potential for data-driven approaches in this area, in which the uncertainty characteristics of subgrid scale processes are derived from observational or high-resolution model data sets (Christensen, Reference Christensen2020). In this article, we discuss the potential for ML to transform stochastic parametrization. In Section 2, we provide the physical motivation for stochastic parametrizations and give an overview of their benefits and limitations. In Section 3, we discuss the potential for ML and highlight some preliminary studies in this space. We conclude in Section 4 by issuing an invitation to the ML parametrization community to move toward such a probabilistic framework.
2. Stochastic parametrization
2.1. Deterministic versus stochastic closure
The conceptual framework utilized by the ML parametrizations typically mirrors that of the schemes they replace. The Navier-Stokes and thermodynamic equations, which describe the atmosphere (and ocean), are discretized onto a spatial grid. The resultant grid-scale variables of state (e.g. temperature, horizontal winds, and humidity in the atmospheric case) for a particular location in space and time provide inputs to the parametrization schemes. The tendencies in these variables over one time step are computed by each scheme. The schemes are deterministic, local in horizontal space and time, but generally nonlocal in the vertical, and thus can be thought of as acting within a subgrid column [for a review, see (Christensen and Zanna, Reference Christensen and Zanna2022)].
Deterministic parametrization schemes typically assume that the grid box is large enough to contain many examples of the unresolved process while simultaneously being “small enough to cover only a fraction of a large-scale disturbance” (Arakawa and Schubert, Reference Arakawa and Schubert1974). The parametrization scheme is then tasked with computing the mean impact of a large ensemble of small-scale phenomena, all experiencing the same background state, onto the resolved scales: a well-posed problem. However, the Navier-Stokes equations are scale invariant (Lovejoy and Schertzer, Reference Lovejoy and Schertzer2013), leading to the emergence of power-law behavior in fluid flows, including in the atmosphere (Nastrom and Gage, Reference Nastrom and Gage1985) and oceans (Storer et al., Reference Storer, Buzzicotti, Khatri, Griffies and Aluie2022). In other words, fluid motions are observed at a continuum of scales, and the spectral gap between resolved and unresolved scales required by deterministic parametrization schemes does not exist. There will always be variability in the real flow on scales similar to the truncation scale, such that it is not possible to determine the impact of the subgrid processes back on the grid-scale with certainty: the grid-scale variables cannot fully constrain the subgrid motions. Deterministic parametrizations will always be a source of error in predictions.
Evidence supporting these theoretical considerations can be provided by coarse-graining studies. For example, Christensen (Reference Christensen2020) takes a km-scale simulation that accurately captures small-scale variability as a reference. This simulation is coarse-grained to the resolution of a typical NWP model and used to initialize a low-resolution forecast model which uses deterministic parametrization schemes. The true evolution of the coarse-grained high-resolution model is compared to that predicted by the forecast model. For a given deterministic forecast tendency, the high-resolution simulation shows a distribution of tendencies, as shown in Figure 1. While the mean of this distribution is captured by the parametrized model, there is substantial variability about the mean, which is not captured.

Figure 1. Coarse-graining studies provide evidence for stochastic parametrizations. (a), the pdf of ‘true’ subgrid temperature tendencies derived from a high-resolution simulation is conditioned on the tendency predicted by a deterministic forecast model (
![]() $ {T}_{fc} $
: colors in legend). (b) Mean ‘true’ tendency conditioned on
$ {T}_{fc} $
: colors in legend). (b) Mean ‘true’ tendency conditioned on
![]() $ {T}_{fc} $
. For this forecast model, positive temperature tendencies are well calibrated, while negative temperature tendencies are biased cold. (c) Standard deviation of “true” tendency conditioned on
$ {T}_{fc} $
. For this forecast model, positive temperature tendencies are well calibrated, while negative temperature tendencies are biased cold. (c) Standard deviation of “true” tendency conditioned on
![]() $ {T}_{fc} $
. For this forecast model, the uncertainty in the “true” tendency increases with the magnitude of the low-resolution forecast tendency. Figure adapted from (Christensen, Reference Christensen2020).
$ {T}_{fc} $
. For this forecast model, the uncertainty in the “true” tendency increases with the magnitude of the low-resolution forecast tendency. Figure adapted from (Christensen, Reference Christensen2020).
Stochastic parametrizations provide an alternative paradigm to deterministic schemes. Instead of representing the mean subgrid tendency, a stochastic approach represents one possible realization of the subgrid scale process (Arnold et al., Reference Arnold, Moroz and Palmer2013). This means a stochastic scheme can be constructed to capture the variability observed in high-resolution datasets but missing from deterministic schemes (Buizza et al., Reference Buizza, Miller and Palmer1999), as shown in Figure 1.
To design a stochastic parametrization, a probability distribution must be specified, which represents the distribution of possible subgrid scale processes, which can be conditional on the observed scale state. A random number is then generated and used to draw from the modeled distribution. Importantly, spatio-temporal correlations can be included in the draw. The resultant parametrization is no longer a subgrid scheme, but a sur-grid scheme, being nonlocal in space and time. This is better able to capture the scale invariance of the Navier-Stokes equations (Palmer, Reference Palmer2019). Evidence for the optimal spatio-temporal correlation scales can be provided by coarse-graining studies (Christensen, Reference Christensen2020).
We stress that it is impossible to know what the true subgrid tendency would have been. A stochastic scheme acknowledges this. Different calls to the stochastic scheme will produce different tendencies, for example, at different points in time in the model integration or in different realizations of an ensemble forecast. It is then possible to assess how the uncertainty in the parametrized subgrid tendency interacts with the rest of the model physics and ultimately leads to differences in the forecast. For this reason, we commonly refer to stochastic parametrizations as representing model uncertainty.
2.2. Benefits of stochastic parametrizations for weather and climate prediction
In Section 2.1, we argued that deterministic parametrization inevitably leads to errors in the predicted subgrid tendencies and that stochastic approaches allow us to capture the true variability in the impact of the subgrid scales. It is important to highlight that this is not simply a theoretical nicety but instead has large implications for the skill of the forecast model. This is because these small-scale errors in the forecast will not remain confined to the smallest scales. Instead, the chaotic nature of the atmosphere means errors will exponentially grow in time and cascade upscale in space (Lorenz, Reference Lorenz1969), causing model simulations to diverge substantially from the true atmosphere.
Since errors in our forecasts are inevitable, instead of a single “best guess” prediction, operational centers typically make a set (or “ensemble”) of equally likely weather forecasts (Bauer et al., Reference Bauer, Thorpe and Brunet2015). The goal is to produce a reliable forecast in which the observed evolution of the atmosphere is indistinguishable from individual ensemble members (Wilks, Reference Wilks2006). To generate the ensemble, the initial conditions of the members are perturbed to represent uncertainties in estimates of the current state of the atmosphere. However, if only initial condition uncertainty is accounted for, the resultant ensemble is overconfident, such that the observations routinely fall outside of the ensemble forecast. A reliable forecast must also account for model uncertainty (Buizza et al., Reference Buizza, Miller and Palmer1999). Stochastic parametrizations have transformed the reliability of initialized forecasts (Buizza et al., Reference Buizza, Miller and Palmer1999; Weisheimer et al., Reference Weisheimer, Corti, Palmer and Vitartn.d.; Berner et al., Reference Berner, Achatz, Batte, De La Cámara, Christensen, Colangeli, Coleman, Crommelin, Dolaptchiev and Franzke2017; Ollinaho et al., Reference Ollinaho, Lock, Leutbecher, Bechtold, Beljaars, Bozzo, Forbes, Haiden, Hogan and Sandu2017), and so are widely used across the weather and subseasonal-to-seasonal forecasting communities. New developments in stochastic parametrizations can further improve the reliability of these forecasts (Christensen et al., Reference Christensen, Lock, Moroz and Palmer2017)
Climate prediction is a fundamentally different problem from weather forecasting (Lorenz, Reference Lorenz1975). It seeks to predict the response of the Earth system to an external forcing (greenhouse gas emissions). The goal is to predict the change in the statistics of the weather over the coming decades, as opposed to a specific trajectory. It has been shown that stochastic parametrizations from the weather forecasting community can substantially improve climate models (Berner et al., Reference Berner, Achatz, Batte, De La Cámara, Christensen, Colangeli, Coleman, Crommelin, Dolaptchiev and Franzke2017; Christensen et al., Reference Christensen, Berner, Coleman and Palmer2017; Strommen et al., Reference Strommen, Christensen, Macleod, Juricke and Palmer2019). Including stochasticity in models can improve long-standing biases in the mean state, such as the distribution of precipitation (Strommen et al., Reference Strommen, Christensen, Macleod, Juricke and Palmer2019), as well as biases in climate variability, such as the El Niño–Southern Oscillation (Christensen et al., Reference Christensen, Berner, Coleman and Palmer2017; Yang et al., Reference Yang, Christensen, Corti, von Hardenberg and Davini2019). Some evidence indicates that stochastic parametrizations can mimic the impacts of increasing the resolution of models (Dawson and Palmer, Reference Dawson and Palmer2015; Vidale et al., Reference Vidale, Hodges, Vanniere, Davini, Roberts, Strommen, Weisheimer, Plesca and Corti2021), likely by improving the representation of small-scale variability.
2.3. Current stochastic approaches
Stochastic parametrizations often couple with existing deterministic parametrizations. They can therefore be thought of as representing random errors in the deterministic scheme. One approach, the “Stochastically Perturbed Parametrisation tendencies” (SPPT) scheme, multiplies the sum of the output of the deterministic parametrizations by a spatio-temporally correlated random number with a mean of one (Buizza et al., Reference Buizza, Miller and Palmer1999; Sanchez et al., Reference Sanchez, Williams and Collins2016; Leutbecher et al., Reference Leutbecher, Lock, Ollinaho, Lang, Balsamo, Bechtold, Bonavita, Christensen, Diamantakis and Dutra2017). An alternative approach takes parameters from within the parametrizations schemes and varies these stochastically to represent uncertainty in their values [Stochastically Perturbed Parameters (SPP): (Christensen et al., Reference Christensen, Moroz and Palmer2015; Ollinaho et al., Reference Ollinaho, Lock, Leutbecher, Bechtold, Beljaars, Bozzo, Forbes, Haiden, Hogan and Sandu2017). Both these approaches are holistic (treating all the parametrized processes) but make key assumptions about the nature of model error. Other approaches are more physically motivated. For example, the Plant-Craig scheme (Plant and Craig, Reference Plant and Craig2008) represents convective mass flux as following a Poisson distribution, motivated using ideas from statistical mechanics (Craig and Cohen, Reference Craig and Cohen2006). The scheme predicts the convective mass flux at cloud base, which can be used as the closure assumption in an existing deterministic deep convection scheme. These ideas were subsequently extended for shallow convection by Sakradzija et al. (Reference Sakradzija, Seifert and Dipankar2016).
A common conclusion across stochastic schemes is the need to include spatio-temporal correlations into the stochasticity in order for the scheme to have a significant impact on model skill. The need for correlations from a practical point of view complements the physical justification put forward in Section 2.1. Correlations are typically implemented using a first-order auto-regressive process in time and using a spectral pattern in space (Christensen et al., Reference Christensen, Moroz and Palmer2015; Johnson et al., Reference Johnson, Stockdale, Ferranti, Balmaseda, Molteni, Magnusson, Tietsche, Decremer, Weisheimer and Balsamo2019; Palmer et al., Reference Palmer, Buizza, Doblas-Reyes, Jung, Leutbecher, Shutts, Steinheimer and Weisheimer2009). The correlation scale parameters can be tuned to maximize forecast skill.
3. ML for stochastic parametrization
3.1. Why could ML be useful?
ML solutions are a natural fit for stochastic parametrization. There is a long history of data-driven approaches proposed by the stochastic parametrization research community. For example, Christensen et al. (Reference Christensen, Moroz and Palmer2015) use statistics derived from a data-assimilation approach to constrain the joint distribution of four uncertain parameters in a stochastic perturbed parameter scheme. Alternatively, the Markov Chain–Monte Carlo approaches of Crommelin and Vanden-Eijnden (Reference Crommelin and Vanden-Eijnden2008) and Dorrestijn et al. (Reference Dorrestijn, Crommelin, Siebesma and Jonker2013) begin by clustering high–fidelity data to produce a discrete number of realistic tendency profiles, before computing the conditional transition statistics between the states defined by the cluster centroids. On the other hand, operationally used stochastic parametrizations (e.g. SPPT, SPP) are pragmatic, with only limited evidence for the structure that they assume. There is therefore substantial room for improvement. We note that the cost of existing stochastic parametrizations, such as SPPT, are generally low, so parametrization improvement, not computational speed-up, is the principal goal here.
3.2. Predicting the PDF
Common to deterministic ML parametrizations, stochastic ML schemes must obey physical constraints, such as dependency on resolved-scale variables, correlations between subgrid tendencies, and conservation properties. In addition, there are two further challenges unique to ML for stochastic parametrization. The first is the need to learn the distribution, which represents uncertainty in the process of interest.
One approach is to couple a stochastic ML approach to an existing deterministic parametrization. A sub-component of the existing scheme can be identified, and the uncertainty in that component is represented using an ML framework. For example, Miller et al. (Reference Miller, Stier and Christensensubmitted) developed a probabilistic ML approach to replace a deterministic convection trigger function (see also (Ukkonen and Mäkelä, Reference Ukkonen and Mäkelä2019)). A random forest was trained on large-scale atmospheric variables, such as temperature and humidity, selected from the variational analysis over the Southern Great Plains (USA) observational site (Tang et al., Reference Tang, Tao, Xie and Zhang2019). Since multiple subgrid atmospheric states are possible for single large-scale state, the random forest is used to predict the probability of convection occurrence thereby capturing uncertainty in the convective trigger. Figure 2 shows the reliability curve for the random forest estimates of convection occurrence. For this dataset, the random forest produced reliable convection estimates (i.e. the predicted probabilities match the conditional observed frequency of convection) with minimal hyperparameter adjustment (Miller et al., Reference Miller, Stier and Christensensubmitted). This is potentially because of the random forest’s feature bootstrapping and ensemble averaging methods. In addition, the random forest assigned a relatively even distribution of predicted probabilities greater than zero (Figure 2), indicating good resolution. Having trained a skillful and reliable model, explainable ML methods can be used to learn about the predictability of unresolved processes such as convection (Miller et al., Reference Miller, Stier and Christensensubmitted). In general, both random forests and neural networks have been found to produce reliable probabilities without postprocessing calibration, in comparison to other ML methods (Niculescu-Mizil and Caruana, Reference Niculescu-Mizil and Caruana2005).
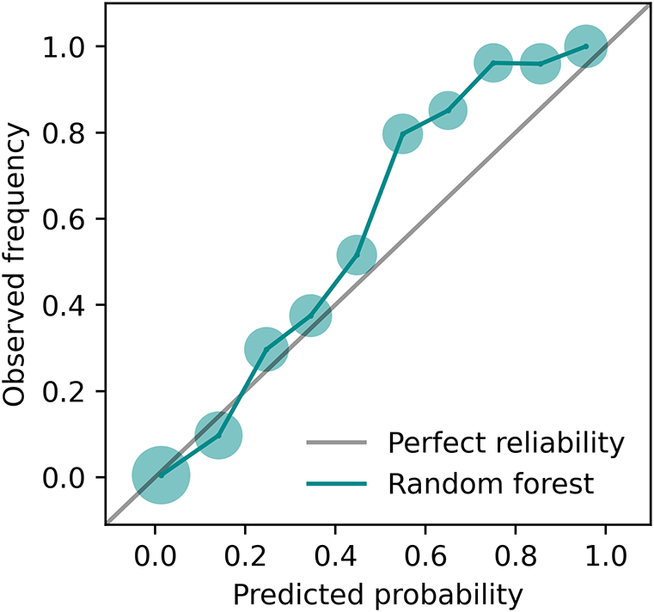
Figure 2. Reliability curve for convection occurrence estimated by the random forest (green line), which is close to perfect reliability (grey line). The random forest was developed for use as a stochastic convection trigger function. The circle sizes are proportional to the log of the number of samples per bin; there are many more non-convection events (91%) than convection events (9%). Figure adapted from Miller et al. (Reference Miller, Stier and Christensensubmitted).
Instead of coupling to an existing parametrization, an alternative approach is to replace a conventional parametrization with an ML approach, which generates samples from the subgrid distribution, conditioned on the grid-scale variables. For example, Guillaumin and Zanna (Reference Guillaumin and Zanna2021) model subgrid momentum forcing using a parametric distribution, and train a neural network to learn the state-dependent parameters of this distribution (Guillaumin and Zanna, Reference Guillaumin and Zanna2021). The distribution is then sampled from during model integration (Cheng et al., Reference Cheng, Perezhogin, Gultekin, Adcroft, Fernandez-Granda and Zannan.d.). Alternatively, Gagne et al. (Reference Gagne, Christensen, Subramanian and Monahan2020) use a generative adversarial network (GAN) to generate samples conditioned on the resolved scale variables. When tested in online mode, the GAN was found to outperform baseline stochastic models and could produce reliable weather forecasts in a simple system. Nadiga et al. (Reference Nadiga, Sun and Nash2022) extend this work and demonstrate that a GAN trained using atmospheric reanalysis data can generate realistic profiles in offline tests. However, it is not known whether a GAN truly learns the target distribution (Arora et al., Reference Arora, Risteski and Zhang2018). Behrens et al. (Reference Behrens, Beucler, Iglesias-Suarez, Yu, Gentine, Pritchard, Schwabe and Eyring2024) train a Variational Encoder-Decoder (VED) network to represent unresolved moist-physics tendencies derived from a superparametrised run with the community atmosphere model: variability in the output profiles is generated by perturbing in the latent space of the encoder–decoder, giving improvements over a simple monte-carlo dropout approach.
Learning to predict the subgrid distribution is not sufficient for the implementation of a stochastic ML scheme. The second half of the problem concerns how to draw from the predicted distribution. Implementations of ML stochastic parametrizations to date have not generally addressed this half of the problem. For example, Cheng et al. (Reference Cheng, Perezhogin, Gultekin, Adcroft, Fernandez-Granda and Zannan.d.) choose to use noise uncorrelated in space and time to implement the mesoscale eddy parametrization of Guillaumin and Zanna (Reference Guillaumin and Zanna2021) in the Modular Ocean Model. Behrens et al. (Behrens et al., Reference Behrens, Beucler, Iglesias-Suarez, Yu, Gentine, Pritchard, Schwabe and Eyring2024) also use uncorrelated noise to sample from the VED network, which could explain the muted impact observed when using the scheme. In contrast, Gagne et al. (Gagne et al., Reference Gagne, Christensen, Subramanian and Monahan2020) feed correlated noise into their GAN to draw from the generator, though the characteristics of this noise, including standard deviation and correlation statistics, were tuned according to forecast skill and not learnt from the data.
3.3. Spatio-temporal correlations
The second key challenge is developing an ML approach to capture the correlations in subgrid tendencies across neighboring columns in space and time while still being practical to implement in a climate model. Any skillful ML approach must address this challenge.
Some early work has addressed temporal correlations. For example, Shin and Baik (Shin and Baik, Reference Shin and Baik2022) modeled entrainment into convective clouds as a stochastic differential equation with parameters predicted by NNs. The resultant solution is analogous to the first-order autoregressive models widely used in stochastic parametrizations but for the case of continuous time. Alternatively, Parthipan et al. (Parthipan et al., Reference Parthipan, Christensen, Hosking and Wischik2023) use recurrent neural networks (RNNs) in a probabilistic framework to learn the temporal characteristics of subgrid tendencies in a toy atmospheric model. An RNN is a natural data-driven extension to simple autoregressive models. It can learn nonlinear temporal associations and also learn how many past states to use when predicting future tendencies. Parthipan et al. (Reference Parthipan, Christensen, Hosking and Wischik2023) found that using an RNN to model the temporal dependencies resulted in improved performance over a first-order auto-regressive baseline (Gagne et al., Reference Gagne, Christensen, Subramanian and Monahan2020). This indicates that more complex correlation structures may improve forecasts in atmospheric models.
Spatial correlations are arguably more difficult to address. This is because of the need to implement any scheme in a model where subgrid columns are typically treated independently at integration stage, and the model is parallelized accordingly. However, inspiration can be taken from the approaches used in existing stochastic parametrization schemes. For example, the Neural GCM NWP emulator (Kochkov et al., Reference Kochkov, Yuval, Langmore, Norgaard, Smith, Mooers, Klöwer, Lottes, Rasp, Düben, Hatfield, Battaglia, Sanchez-Gonzalez, Willson, Brenner and Hoyer2024) uses spatio-temporally correlated fields much like those used in operational models to perturb the learnt physics module. The spatio-temporal scales were optimized during training, though most changed very little from their initialized values. Alternatively, Bengtsson et al. (Bengtsson et al., Reference Bengtsson, Körnich, Källén and Svensson2011; Bengtsson et al., Reference Bengtsson, Steinheimer, Bechtold and Geleyn2013) have used a “game of life” cellular automaton (CA: Figure 3. a) to generate correlated fields for use in convection parametrization. The CA operates on a grid finer than that used by the model parametrizations, such that each CA grid cell represents one convective element. The CA self-organises in space and persists in time, introducing spatio-temporal correlations which can be coupled to an existing deterministic convection scheme (Bengtsson et al., Reference Bengtsson, Steinheimer, Bechtold and Geleyn2013). However, the spatial correlations generated through this approach are extremely difficult to tune by hand (L. Bengtsson, pers. comm., 2018). One possible ML approach is to use a genetic algorithm (GA), which breeds and mutates successful rule sets, to navigate the large rule space. By using a fitness function based on the fractal dimension of the state after a certain number of model steps [e.g. following Christensen and Driver, Reference Christensen and Driver2021], a GA can discover cellular automata that produce a distribution of cells that more closely match those observed in clouds, as shown in Figure 3. Further work is needed to fully explore this possibility.

Figure 3. a. The classic cellular automata, the game of life, after 70 rule iterations on random initial conditions. b. A set of rules discovered through the use of a genetic algorithm after 70 iterations from a random initial condition. c. An example of fitness convergence for a genetic algorithm scheme.
An alternate approach to address spatial correlations incorporates information from neighboring grid cells, as is utilized in the stochastic convection scheme of Plant and Craig (Plant and Craig, Reference Plant and Craig2008) or in the deterministic convolutional neural network proposed by Wang et al. (Wang et al., Reference Wang, Yuval and O’Gorman2022). Here, accuracy gain from nonlocal inputs may be found to outweigh the increase in computational cost.
3.4. Structure
The question of finding the optimal structure for an ML model is common to all domains. Whilst tremendous success has come in the language domain from transformer-based models (Vaswani et al., Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser and Polosukhin2017), the same tools have not similarly transformed the modeling of continuous processes. In fact, in the physical domain, there is an ongoing search for the most appropriate architecture. For example, the data-driven NWP model GraphCast (Lam et al., Reference Lam, Sanchez-Gonzalez, Willson, Wirnsberger, Fortunato, Pritzel, Ravuri, Ewalds, Alet and Eaton-Rosen2022) uses a graph neural network as the backbone, while FourCastNet (Pathak et al., Reference Pathak, Subramanian, Harrington, Raja, Chattopadhyay, Mardani, Kurth, Hall, Li and Azizzadenesheli2022) and Pangu-Weather (Bi et al., Reference Bi, Xie, Zhang, Chen, Gu and Tian2023) each develop separate inductive biases to use on top of a transformer backbone.
This problem is also encountered when building stochastic ML parametrizations. For example, developing a custom ML architecture was key when developing a probabilistic ML parametrization for cloud cover for the European Centre for Medium-range Weather Forecasts single-column model (SCM) (Parthipan, Reference Parthipan2024). It was found that a simple feed-forward neural network struggled to create and remove clouds appropriately. This is because transitions between cloud-containing and cloudless states are relatively rare in the training data. One solution to this problem was to use a mixed continuous-discrete model, which separated the task into i) predicting the probability of a cloud-containing state and ii) given a cloud-containing state, predicting the amount of cloud. Such models are often used for situations when the probability distribution has a discrete spike at the origin combined with a continuous positive distribution (Weld and Leemis, Reference Weld and Leemis2017). Figure 4 shows how this improvement in ML model structure results in substantial improvements in predicted cloud cover. However, this was a bespoke solution for the chosen problem. It is not clear whether a general architectural leap could bring enormous benefits to the field of physical modeling, as the transformer did for language.
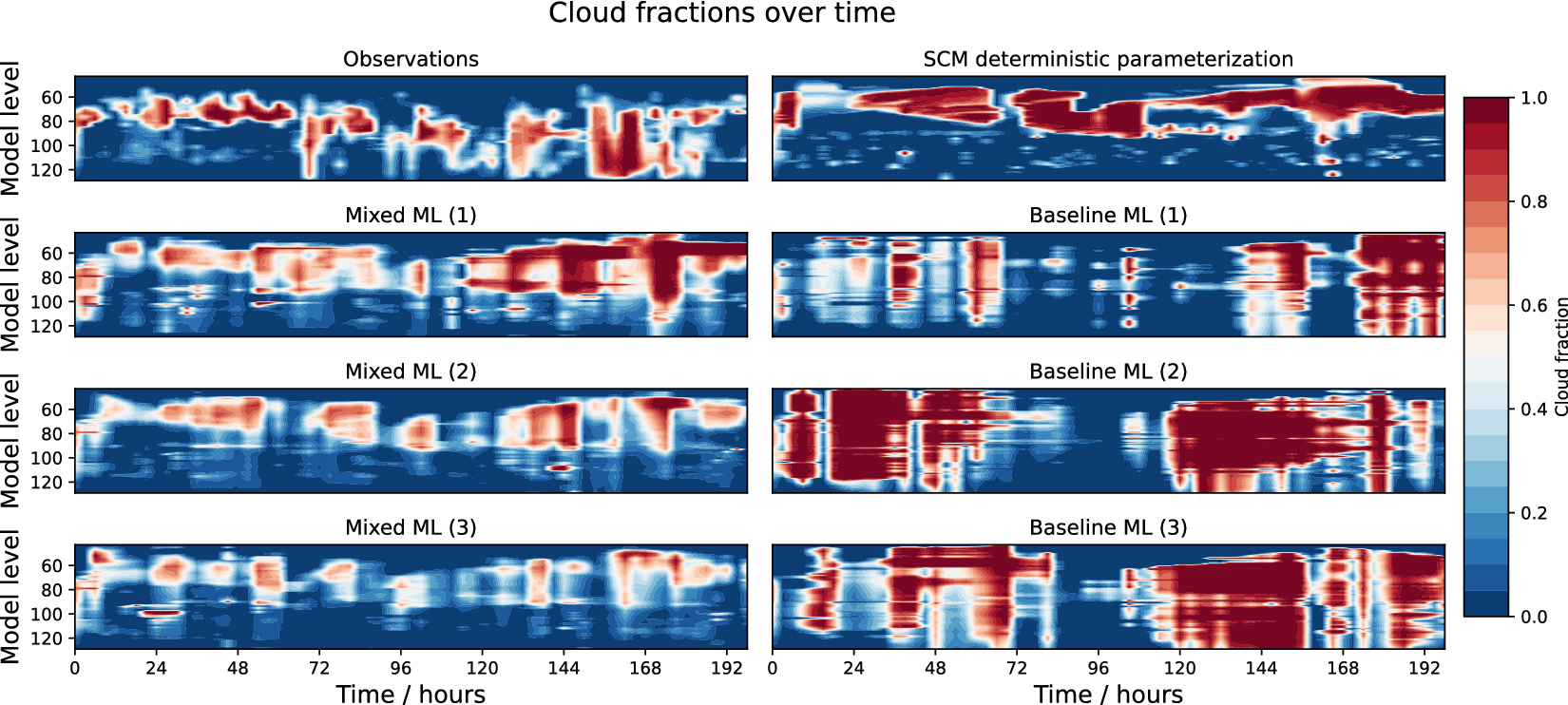
Figure 4. Cloud fractions as a function of height (model levels) for forecasts of 200 hours. Observed cloud fraction is compared to that from the operational deterministic parametrization, and to two stochastic ML models. The Baseline ML model is a simple feed-forward neural network, whilst the Mixed ML model separates the task of modeling into a binary categorization and continuous prediction problem. These are probabilistic models, and three sampled trajectories are shown for both. The mixed model is better able to create and remove cloud. Adapted from Parthipan (Reference Parthipan2024).
4. Conclusions
Sub-grid parametrizations are a large source of error in weather and climate forecasts. ML is transforming this field, leading to reduced errors and large speed-ups in model predictions. However, a key widely used assumption in ML parametrization is that of determinism. We have argued that this assumption is flawed and that substantial progress could be made by moving to a probabilistic framework. We discuss the first attempts to develop such stochastic ML parametrizations and highlight remaining challenges including learning sur-grid correlation structures and suitable architectures. Fortunately, ample training data exists to learn such probabilistic parametrizations. The high-resolution datasets, which are coarse-grained and used to train deterministic ML parametrizations are suitable for this task [e.g. Brenowitz et al., Reference Brenowitz, Beucler, Pritchard and Bretherton2020; Yuval and O’Gorman, Reference Yuval and O’Gorman2020; Beucler et al., Reference Beucler, Gentine, Yuval, Gupta, Peng, Lin, Yu, Rasp, Ahmed, O’Gorman, Neelin, Lutsko and Pritchard2021]. In addition, a new multi-model training dataset is in production as part of the Model Uncertainty Model Intercomparison Project (MUMIP: https://mumip.web.ox.ac.uk), which will be ideal for ML stochastic parametrizations. Exploring this dataset will be the focus of future work.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/eds.2024.45.
Author contribution
Conceptualization, supervision: HC; investigation, methodology, software, visualization, writing—original draft, and writing—review and editing: HC, SK, GM, RP. All authors approved the final submitted draft.
Competing interest
None
Data availability statement
The coarse-grained data used in Figure 1 are archived at the Centre for Environmental Data Analysis (http://catalogue.ceda.ac.uk/uuid/bf4fb57ac7f9461db27dab77c8c97cf2). The ARM variational analysis dataset used to produce Figure 2 can be downloaded from https://www.arm.gov/capabilities/science-data-products/vaps/varanal. The cloud fraction experiments in Figure 4 were run using the ECMWF OpenIFS single-column model version 43r3, available for download from https://confluence.ecmwf.int/display/OIFS.
Provenance statement
This article is part of the Climate Informatics 2024 proceedings and was accepted in Environmental Data Science on the basis of the Climate Informatics peer review process.
Funding statement
SK and GM were supported by the UK National Environmental Research Council Award NE/S007474/1. GM further acknowledges the University of Oxford Clarendon Fund. RP was funded by the Engineering and Physical Sciences Research Council grant number EP/S022961/1. HC was supported by UK Natural Environment Research Council grant number NE/P018238/1, by a Leverhulme Trust Research Leadership Award and through a Leverhulme Trust Research Project Grant “Exposing the nature of model error in weather and climate models.” This publication is part of the EERIE project (Grant Agreement No 101081383) funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Climate Infrastructure and Environment Executive Agency (CINEA). Neither the European Union nor the granting authority can be held responsible for them. HC’s contribution to EERIE is funded by UK Research and Innovation (UKRI) under the UK government’s Horizon Europe funding guarantee (grant number 10049639).
Ethical standard
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.









Comments
Dear Editor,
I can confirm this paper has already undergone review for the Climate Informatics 2024 conference. I uploaded a brief response to reviewers comments with my other files. No changes were required.
All the best,
Hannah