1. Introduction
Attaining sustainable agriculture entails the pursuance of resilient agricultural practices that support synergies in increasing agricultural productivity and maintaining the ecosystem. This requires judicious use of farm inputs including fertilizers. With the ever-growing human population, the demand for fertilizers, especially nitrogen (N) fertilizers to support food production, will continue to increase. Erisman et al. (Reference Erisman, Sutton, Galloway, Klimont and Winiwarter2008) note that, while over 78 per cent of the atmosphere is composed of nitrogen, the supply of N fertilizers in commercial quantities is mainly facilitated through the Haber–Bosch process of industrial ammonia synthesis. Galloway et al. (Reference Galloway, Townsend and Erisman2008) indicate that about 80 per cent of nitrogen from the Haber–Bosch process is used in the production of mineral fertilizers.
In spite of the tremendous benefits from the Haber–Bosch process, it is estimated that only half of the fertilizers applied to crops are utilized, and the rest lost to the atmosphere, soil and aquatic ecosystems (Galloway et al., Reference Galloway, Townsend and Erisman2008). The unintended consequence from the Haber–Bosch process has been linked to some negative environmental externalities, including increases in air and water pollution. Notwithstanding the potential adverse impacts of fertilizers, estimates show that global fertilizer consumption is expected to increase from about 183 to 201 million metric tonnes between 2013 and 2018, with about 60 per cent share from N fertilizers. Although fertilizer application rates are currently low in Sub-Saharan Africa (SSA), the use of N fertilizers is projected to double within this same period (FAO, 2015).
Given that maize is a staple crop in many countries in SSA including Zambia, significant amounts of fertilizers are normally applied to increase maize output in order to meet demand in the region. While output growth is required to meet the increasing demand for food in SSA, continuous increases in fertilizer use without considering options to mitigate losses from runoff, leaching and volatilization of N fertilizers could have negative environmental consequences.
Dobermann and Cassman (Reference Dobermann and Cassman2002) point out that, with good management practices, nitrogen recovery from maize could be improved from 37 to 80 per cent, suggesting the relevance of enhanced agricultural technologies in mitigating greenhouse gas (GHG) emissions in the coming years. In line with the Nebraska declaration on conservation agriculture and other conventions, conservation agriculture (CA)Footnote 1 is regarded as one technology that could enhance food productivity and environmental efficiency (EE) relative to conventional farming (Stevenson et al., Reference Stevenson, Serraj and Cassman2014). The FAO (2010) describes CA as a concept for resource-saving agricultural crop production which strives to achieve acceptable profits through higher and sustained production levels, and concurrently conserving the natural environment. Valuing social cost with regard to carbon dioxide emission suggests that CA technology is a potential candidate to harness the desired economic, environmental and social synergies of sustainable agriculture (Wei et al., Reference Wei, White, Hu and Willett2010).
Assessing the environmental impact of CA with particular reference to the utilization of N fertilizers largely depends on the ability to generate a nitrogen balance sheet of quantity of nitrogen (N) consumed in producing the output and quantity of nitrogen that is unutilized (surplus). This may require vigorous laboratory analysis, with complex computer models and technical expertise in modelling soil biogeochemistry and nitrogen dynamics. Hence, some studies account for nitrogen surplus using weights such as the International Panel on Climate Change (IPCC) default value of 1 per cent of N applied or N released through mineralization of organic matter in mineral soils (e.g., the eutrophication power of 1 adopted by Coelli et al., Reference Coelli, Lauwers and Huylenbroeck2007).Footnote 2 However, in their recent study on Mexico, Saynes et al. (Reference Saynes, Delgado, Tebbe, Etchevers, Lapidus and Otero-Arnaiz2014) demonstrate that this approach underestimates nitrogen emission by more than two-fold. Some other related literature employs National Farm Accountancy Data (for example, Reinhard et al., Reference Reinhard, Lovell and Thijssen1999, Reference Reinhard, Lovell and Thijssen2002), while others have used national nutrient management tools (for example, Ramilan et al., Reference Ramilan, Scrimgeour and Marsh2009). In economies such as Zambia there are no standard national nutrient management tools, soil nutrients testing is beyond the reach of many subsistence farmers, and soil testing laboratories are either of lower standards or non-existent. The current study differs from other studies in the generation of farm-level nitrogen balance sheets by using the Nitrogen Index Tier Zero tool (NITZ; developed and validated by Saynes et al., Reference Saynes, Delgado, Tebbe, Etchevers, Lapidus and Otero-Arnaiz2014).Footnote 3
Over the past two decades, numerous studies have analyzed technical efficiency (TE) and allocative efficiency of farmers in SSA (for example, Abdulai and Huffman, Reference Abdulai and Huffman2000). A meta-analysis by Ogundari (Reference Ogundari2014) summarizes the findings of these studies. What is clearly missing is an examination of the environmental externalities of agricultural production in this region. This study contributes to the literature by examining the impact of CA technology on the EE of maize farmers in Zambia. In particular, it explores crop utilization of N fertilizers among farms practising CA and conventional farming technologies. We also consider potential technology heterogeneity among these farms and employ a multi-stage approach to examine EE in a meta-frontier (MF) framework, while correcting for selection bias that may arise from both observable and unobservable factors.
Although the study follows TE and EE estimation strategies, it is unique in several ways (for example, Reinhard et al., Reference Reinhard, Lovell and Thijssen2002; Nguyen et al., Reference Nguyen, Hoang and Seo2012; Rao et al., Reference Rao, Brümmer and Qaim2012). First, it differs from other productivity and efficiency studies on CA that assume a common technology for all production units by accounting for technology heterogeneity among farm households (for example, Ng'ombe and Kalinda, Reference Ng'ombe and Kalinda2015). In spite of recent applications of a selectivity-corrected stochastic frontier model in efficiency measurement, this study is the first to employ the framework in the estimation of EE (for example, Bravo-Ureta et al., Reference Bravo-Ureta, Greene and Solis2012; González-Flores et al., Reference González-Flores, Bravo-Ureta, Solís and Winters2014; Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015). As in González-Flores et al. (Reference González-Flores, Bravo-Ureta, Solís and Winters2014) and Villano et al. (Reference Villano, Bravo-Ureta, Solis and Fleming2015), we use both the propensity score matching (PSM) method and Greene's (Reference Greene2010) sample selection approach to address these issues in a MF framework. To the best of our knowledge, this is also the first study to employ the NITZ tool data set within a frontier framework.
The rest of the paper is organized as follows. In section 2, CA from the perspective of Zambia is described. Sections 3 and 4 discuss the conceptual framework and the analytical strategy employed, respectively. The data and empirical specification are presented in section 5, while section 6 discusses the empirical results. The final section presents conclusions and policy recommendations.
2. Conservation agriculture in Zambia
There are three main CA implementing agencies in Zambia: namely, the government through the FAO and the Ministry of Agriculture and Livestock (MAL); the Zambian National Farmers Union (ZNFU); and other agencies broadly regarded as non-governmental organizations. The ZNFU considers CA as an integrated technology with three main linked principles, namely: minimum soil disturbance; maintenance of permanent or semi-permanent organic soil cover; and diversification of crop species. The CA technology entails localizing tillage and fertilizers in permanent rip lines or planting stations, ensuring adequate weed control, retaining crop residues and intercropping, or rotating crops with nitrogen-fixing legumes.
The ZNFU also promotes the cropping of complementary perennial vegetation such as Faiderbia albida (a leguminous tree), and live fences. Completing land preparation before the onset of planting rains is equally considered a critical CA technology requirement in Zambia, in order to take advantage of nitrogen flush and to reduce the waiting time to planting. In particular, Haggblade and Tembo (Reference Haggblade and Tembo2003) indicate that, on the onset of the first possible planting rains, maize yields decline by 1–2 per cent for each day of delayed planting. CA technology therefore ensures that these losses are reduced to a minimum, thus contributing to higher output and improving food and nutrition security, as well as reducing environmental degradation in Zambia (Neubert, Reference Neubert2011).
3. Conceptual framework
The conceptual framework used in this study follows the Law of Conservation of Mass, which states that matter can be changed from one form to another, mixtures can be made or separated, and pure substances can be decomposed, but the total amount of mass remains constant. In effect, the total quantity of N fertilizers applied in a system is fixed, only part of it may contribute to the generation of the farm output, and the surplus may be environmentally detrimental. More importantly, as much as nitrogen is a macro-nutrient for maize, reactive nitrogen cascade from leaching, runoff and volatilization of synthetic nitrogen tend to modify the balance of GHG. It also decreases stratospheric ozone, increases soil acidification, enhances tropospheric ozone, and catalyzes the formation of secondary particulates in the atmosphere (Erisman et al., Reference Erisman, Sutton, Galloway, Klimont and Winiwarter2008). More so, nitrous oxide (N2O) is considered one of the major non-CO2 GHG emitters, with agriculture regarded as the biggest anthropogenic source (Reay et al., Reference Reay, Davidson, Smith, Smith, Melillo, Dentener and Crutzen2012). For instance, in 2005 emissions from agricultural activities, largely from soil tillage and application of N fertilizers, accounted for approximately 60 per cent of total global anthropogenic emissions of N2O (Smith et al., Reference Smith, Metz, Davidson, Bosch, Dave and Meyer2007).
In essence, it might be problematic to quantify the exact economic and environmental consequences of inputs such as N fertilizers. However, the ability to reasonably establish a nitrogen balance sheet at the farm level with respect to nitrogen recovered and nitrogen surplus is an indication of the potential economic benefits and environmental burden that may arise from the application of N fertilizers. Here, the NITZ tool is used in generating the nitrogen balance. Saynes et al. (Reference Saynes, Delgado, Tebbe, Etchevers, Lapidus and Otero-Arnaiz2014) are the first to use it in their study of N2O emissions from N fertilizer in Mexico based only on nutrient management practices. In this study, we argue that, beyond nutrient management practices, other farm and household confounding factors may influence household nitrogen use efficiency. We therefore examine household EE with respect to nitrogen efficiency, using nitrogen balance scores from the NITZ tool in a stochastic production frontier (SPF) framework. Figure A1, available in the online appendix at (https://doi.org/10.1017/S1355770X16000309), displays quantitative and qualitative results of the NITZ (see Saynes et al., Reference Saynes, Delgado, Tebbe, Etchevers, Lapidus and Otero-Arnaiz2014 for details on the implementation of the NITZ).Footnote 4
In empirical analysis of EE, the potential environmentally detrimental element is either considered an input, with input-orientation strategies (for example, Reinhard et al., Reference Reinhard, Lovell and Thijssen1999, Reference Reinhard, Lovell and Thijssen2002) or an output, and efficiency estimates follow an output orientation (for example, Färe, Reference Färe, Grosskopf, Lovell and Pasurka1989; Cuesta et al., Reference Cuesta, Lovell and Zofio2009). On assuming weak disposability in the output orientation, an extra pollution variable is incorporated into the production model and estimated by distance and directional functions. For instance, Färe, (Reference Färe, Grosskopf, Lovell and Pasurka1989) and Cuesta et al. (Reference Cuesta, Lovell and Zofio2009) employed deterministic and stochastic hyperbolic and enhanced hyperbolic distance approaches, respectively. Coelli et al. (Reference Coelli, Lauwers and Huylenbroeck2007) indicate that, although previous applications did not consider material balance in their empirical study, specifications that follow the approach by Färe (Reference Färe, Grosskopf, Lovell and Pasurka1989) violate the material balance condition. Materials balance is fundamentally an adding-up condition, which essentially indicates that ‘what goes in must come out’.
To the extent that nitrogen is applied as an input and only the unexpected surplus may be environmentally detrimental, the material balance of a product like nitrogen is calculated as the amount of nitrogen that enters the farm in inputs minus the amount that leaves the farm bound up in useful output. We follow the input-oriented estimation strategy by Reinhard et al. (Reference Reinhard, Lovell and Thijssen2002), which draws from the material balance framework adopted by Coelli et al. (Reference Coelli, Lauwers and Huylenbroeck2007) for phosphorous. This approach avoids the introduction of an extra pollution variable into the model, be it input or weak disposable bad output. This also complies with the underlying adding-up condition in material balance and demonstrates that environmental pollution can be reduced under efficient use of inputs. This approach is pragmatic, particularly when the potential environmental burden is directly linked to the application of inputs such as N fertilizers.
4. Analytical strategy
This study employs the SPF model to estimate the TE and EE of maize-producing households in Zambia, with the assumption that farmers in our sample exclusively practise either CA technology or otherwise. The SPF model is specified as:
where
![]() ${\bi Y}_{{\bi ij}_{i}}$
denotes a scalar of outputs of farmer i using technology j;
${\bi Y}_{{\bi ij}_{i}}$
denotes a scalar of outputs of farmer i using technology j;
![]() ${\bi X}$
is a vector of inputs and other explanatory variables;
${\bi X}$
is a vector of inputs and other explanatory variables;
![]() ${\bi D}_{\bi C}$
is a dummy variable capturing the effect of CA technology; and
${\bi D}_{\bi C}$
is a dummy variable capturing the effect of CA technology; and
![]() ${\bf \varepsilon}_{\bi ij}$
is the error term, which is composed of
${\bf \varepsilon}_{\bi ij}$
is the error term, which is composed of
![]() ${\bi v}_{\bi ij}$
, the random term (white noise) and
${\bi v}_{\bi ij}$
, the random term (white noise) and
![]() ${\bi u}_{\bi ij}$
, the systematic error term capturing inefficiency (Aigner et al., Reference Aigner, Lovell and Schmidt1977). Given that farmers self-select themselves into adoption and non-adoption, selectivity bias may arise from both observable and unobservable factors.
${\bi u}_{\bi ij}$
, the systematic error term capturing inefficiency (Aigner et al., Reference Aigner, Lovell and Schmidt1977). Given that farmers self-select themselves into adoption and non-adoption, selectivity bias may arise from both observable and unobservable factors.
4.1. Sample selection in stochastic production frontier
PSM is used to construct statistically comparable counterfactual groups of adopters and non-adopters to correct for observable biases from the sample (Abdulai and Binder, Reference Abdulai and Binder2006). This entails using a binary choice model (a Probit model in this case) to generate a propensity score, conditional on pre-treatment observed covariates of adopters and non-adopters, and expressed as
where d i is a binary variable, equal to 1 for adopters and 0 for non-adopters, z is a vector of explanatory variables in the sample selection model, β is a vector of parameters to be estimated, and ω i is the error term in the selection equation (Greene, Reference Greene2010).
In the literature it is assumed that unobserved factors in the PSM model may be correlated with the error term in the SPF model, resulting in selection bias. Sample selection correction models are then employed to correct for sample selection bias due to unobservable factors (for example, Kumbhakar et al., Reference Kumbhakar, Tsionas and Sipilainen2009; Lai et al., Reference Lai, Polachek and Wang2009; Greene, Reference Greene2010). The specifications in these applications are very similar, but differ in their assumptions about how the selection mechanism relates to the error terms. Specifically, Greene (Reference Greene2010) assumes that selection bias is attributable to v
i
, whereas Kumbhakar et al. (Reference Kumbhakar, Tsionas and Sipilainen2009) and Lai et al. (Reference Lai, Polachek and Wang2009) assume selectivity is related to u
i
and
![]() $\varepsilon_{i}$
, respectively. The models by Kumbhakar et al. (Reference Kumbhakar, Tsionas and Sipilainen2009) and Lai et al. (Reference Lai, Polachek and Wang2009) require computationally demanding log likelihood functions (Greene, Reference Greene2010; Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015).
$\varepsilon_{i}$
, respectively. The models by Kumbhakar et al. (Reference Kumbhakar, Tsionas and Sipilainen2009) and Lai et al. (Reference Lai, Polachek and Wang2009) require computationally demanding log likelihood functions (Greene, Reference Greene2010; Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015).
We follow the framework presented by Bravo-Ureta et al. (Reference Bravo-Ureta, Greene and Solis2012) and Villano et al. (Reference Villano, Bravo-Ureta, Solis and Fleming2015), using PSM to correct for biases stemming from observable factors, and Greene's (Reference Greene2010) SPF sample selection correction model to account for selection bias from unobservable factors. Murphy and Topel's (Reference Murphy and Topel2002) correction is employed to adjust the standard errors. Greene (Reference Greene2010) indicates that (
![]() ${\bi Y}{\bi i}\comma \; {\bi X}{\bi i}\rpar $
in equation (1) is observed only when d
i
= 1 in equation (2). The error structure is such that:
${\bi Y}{\bi i}\comma \; {\bi X}{\bi i}\rpar $
in equation (1) is observed only when d
i
= 1 in equation (2). The error structure is such that:
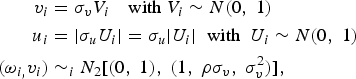 $$\eqalign{v_{i} & = \sigma_{v}V_{i}\quad \hbox{with}\ V_{i}\sim N\lpar 0\comma \; 1\rpar \cr u_{i} & = \vert \sigma_{u}U_{i} \vert =\sigma_{u}\vert U_{i}\vert \; \; \hbox{with}\; \; U_{i}\sim N\lpar 0\comma \; 1\rpar \cr \lpar \omega_{i\comma }v_{i} \rpar & \sim_{i} N_{2}\lsqb \lpar 0\comma \; 1\rpar \comma \; \lpar 1\comma \; \rho \sigma_{v}\comma \; \sigma_{v}^{2}\rpar \rsqb \comma \; } $$
$$\eqalign{v_{i} & = \sigma_{v}V_{i}\quad \hbox{with}\ V_{i}\sim N\lpar 0\comma \; 1\rpar \cr u_{i} & = \vert \sigma_{u}U_{i} \vert =\sigma_{u}\vert U_{i}\vert \; \; \hbox{with}\; \; U_{i}\sim N\lpar 0\comma \; 1\rpar \cr \lpar \omega_{i\comma }v_{i} \rpar & \sim_{i} N_{2}\lsqb \lpar 0\comma \; 1\rpar \comma \; \lpar 1\comma \; \rho \sigma_{v}\comma \; \sigma_{v}^{2}\rpar \rsqb \comma \; } $$
where ρ is the sample selection correction variable for nonlinear models. The model parameters are estimated using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm approach and asymptotic standard errors are obtained using the Berndt–Hall–Hall–Hausman (BHHH) algorithm estimator.Footnote 5 Selectivity bias due to unobservable factors is considered to exist if ρ is statistically significant (Greene, Reference Greene2010).
4.2. Meta-frontier approach
A single production frontier is normally employed to estimate TE and EE when firms use the same technology. Given that adopting CA technology may improve farmers' access to better technology, using a meta-production frontier is a more suitable approach (Hayami and Ruttan, Reference Hayami and Ruttan1985).
Battese et al. (Reference Battese, Rao and O'Donnell2004) developed an MF model for the estimation of technology gaps among producers under different technologies relative to the potential technology available to the whole industry. The MF model facilitates reliable decomposition of efficiency into group specific efficiencies and meta-technology ratio, which enables the interpretation of group efficiency as well as technology gap scores. Following the EE framework of Reinhard et al. (Reference Reinhard, Lovell and Thijssen1999, Reference Reinhard, Lovell and Thijssen2002) and Battese et al.'s (2004) MF logic, we estimate both TE and EE for N fertilizer application in the MF framework. In this framework, EE is measured as the ratio of minimum feasible nitrogen surplus to observed quantities of nitrogen surplus, at given conventional input and output levels (Reinhard et al., Reference Reinhard, Lovell and Thijssen2002).
In this context, an SPF is defined as
where Y ij denotes the output for the i th farm, of the j th group; X ij is a vector of inputs used by the i th farm, under the j th technology; E ij is the quantity of nitrogen surplus of farm i under group j; α j denotes the parameters of the j th technology to be estimated; and v ij and u ij are the random (white noise) and systematic inefficiency error terms, respectively. We assume heteroscedasticity of the one-sided error term (v ij ) to reflect factors under the farmer's control (Caudill and Ford, Reference Caudill and Ford1993).
The deterministic MF model for both CA adopters and non-adopters can be expressed as
where
![]() $Y_{i}^{\ast}$
denotes the output for the MF function, X
i
is a vector of inputs including N fertilizers, and α* denotes the vector of parameters to be estimated.Footnote
6
The observed output for the i
th
firm defined by the SPF for the j
th
group in (4) and (5) is alternatively expressed in terms of the MF function as
$Y_{i}^{\ast}$
denotes the output for the MF function, X
i
is a vector of inputs including N fertilizers, and α* denotes the vector of parameters to be estimated.Footnote
6
The observed output for the i
th
firm defined by the SPF for the j
th
group in (4) and (5) is alternatively expressed in terms of the MF function as
where the first term on the right-hand side in (6) is the TE of farmer i relative to the stochastic frontier of group j.
As in Reinhard et al. (Reference Reinhard, Lovell and Thijssen2002) and Kouser and Qaim (Reference Kouser and Qaim2015), we argue that the logarithm of the output of an environmentally efficient producer can be obtained by replacing the observed quantity of nitrogen surplus (E
i
) in equation (4) with the minimum feasible nitrogen surplus and setting u
i
= 0. Setting equation (4) and the output of the environmentally efficient producer equal, and solving for
![]() $ln{EE}_{i}=lnE_{i}^{\ast}-lnE_{i}$
, yields the EE estimator
$ln{EE}_{i}=lnE_{i}^{\ast}-lnE_{i}$
, yields the EE estimator
 $$\eqalign{ln{EE}_{i} & = \left[-\left(\alpha_{e}+\sum\limits_j {\alpha_{je}lnX_{ij}lnE_{i}} \right)\pm \left\{\left(\alpha_{e}+\sum\limits_j {\alpha_{je}lnX_{ij}lnE_{i}} \right)\right.\right. \cr & \quad\left.\left. -2\alpha_{ee}u_{i}\vphantom{\sum_0^{1}}\right\}^{0.5}\right]\Bigg/\alpha_{ee}.} $$
$$\eqalign{ln{EE}_{i} & = \left[-\left(\alpha_{e}+\sum\limits_j {\alpha_{je}lnX_{ij}lnE_{i}} \right)\pm \left\{\left(\alpha_{e}+\sum\limits_j {\alpha_{je}lnX_{ij}lnE_{i}} \right)\right.\right. \cr & \quad\left.\left. -2\alpha_{ee}u_{i}\vphantom{\sum_0^{1}}\right\}^{0.5}\right]\Bigg/\alpha_{ee}.} $$
In this case, we calculate EE by assuming a positive squared root term in equation (8)Footnote 7 . The EE estimation is simply a mathematical derivation of equation (4) at full efficiency. In relation to the MF, the EE of farmer irelative to the stochastic frontier of j th can be expressed as
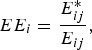 $$EE_{i}=\displaystyle{{E^{\ast}_{ij}} \over {E_{ij}}}\comma \; $$
$$EE_{i}=\displaystyle{{E^{\ast}_{ij}} \over {E_{ij}}}\comma \; $$
where E* is the minimum feasible nitrogen surplus and E is the observed quantity of nitrogen surplus as in equation (7).
The second term on the right-hand side of equation (6) is the MF technology ratio (MTR) for farmer i in group j, and can be expressed as
The TEs and EEs relative to the MF functions are therefore a product of group-specific TEs and EEs and the MTR. TEs and EEs of the MF are then expressed as
The MTR captures productivity and EE differences between CA and non-CA adopters and lies between 0 and 1.
We obtain the MF parameters by either minimizing the sum of the squared, or sum of the absolute deviation of the distance between the MF and the group frontiers at the observed vector of inputs for farms in the groups (Battese et al., Reference Battese, Rao and O'Donnell2004).Footnote 8 This involves solving the optimization equation below:
 $$\eqalign{min\; \; L & \equiv \sum \sum\limits_{i=1}^N {\lpar \hbox{ln}\; f\lpar X_{i}}\comma \; E_{i}\comma \; \alpha^{\ast}\rpar - \hbox{ln}\; f\lpar X_{i}\comma \; E_{i}\comma \; \hat{\alpha}_{j}\rpar \rpar ^{2} \cr s.t.\ln f\lpar X_{i}\comma \; E_{i}\comma \; \alpha^{\ast}\rpar & \ge \ln f\lpar X_{i}\comma \; E_{i}\comma \; \hat{\alpha}_{j}\rpar \; \; for\; all\; \; i} $$
$$\eqalign{min\; \; L & \equiv \sum \sum\limits_{i=1}^N {\lpar \hbox{ln}\; f\lpar X_{i}}\comma \; E_{i}\comma \; \alpha^{\ast}\rpar - \hbox{ln}\; f\lpar X_{i}\comma \; E_{i}\comma \; \hat{\alpha}_{j}\rpar \rpar ^{2} \cr s.t.\ln f\lpar X_{i}\comma \; E_{i}\comma \; \alpha^{\ast}\rpar & \ge \ln f\lpar X_{i}\comma \; E_{i}\comma \; \hat{\alpha}_{j}\rpar \; \; for\; all\; \; i} $$
By minimizing the objective function (
![]() $L^{\ast} \equiv {\bar X}\alpha^{\ast}\rpar $
, equation (12) can be solved, subject to the linear restrictions, where
$L^{\ast} \equiv {\bar X}\alpha^{\ast}\rpar $
, equation (12) can be solved, subject to the linear restrictions, where
![]() ${\bar X}$
is the mean of
x
-vector elements for all observations.Footnote
9
Here,
${\bar X}$
is the mean of
x
-vector elements for all observations.Footnote
9
Here,
![]() ${\hat \alpha}_{j}$
is treated as fixed, so that the second term in the summation is constant with respect to the minimization. By simulation, the standard errors for the MF parameters can be estimated (Battese et al., Reference Battese, Rao and O'Donnell2004).
${\hat \alpha}_{j}$
is treated as fixed, so that the second term in the summation is constant with respect to the minimization. By simulation, the standard errors for the MF parameters can be estimated (Battese et al., Reference Battese, Rao and O'Donnell2004).
5. Data and specification
The data used in this study are drawn from a recent farm household survey conducted between August and November 2013 in the Central, Eastern, Western and Southern provinces of Zambia. These provinces contribute more than 60 per cent to maize production in Zambia and are considered the prominent CA technology provinces.Footnote 10 A multi-stage sampling technique was employed to select 407 farm households across 12 districts in these provinces. In the first stage, all four provinces were purposively selected, such that there would be equal opportunity for all CA technology farmers in these provinces to be included in the sample. Each province became a stratum, and in consultation with farmers and extension agents, and also given that there were no differences in the estimated number of adopters in all provinces, three districts each were randomly selected per province. In each district, five agricultural campsFootnote 11 were then randomly drawn, within which three farmer groups were randomly selected. Individual CA farmers and their non-CA counterparts were then randomly selected from the groups.
Face-to-face interviews were conducted with the selected farmers by enumerators who spoke both English and the local language, and supervised by one of the authors, using a detailed structured questionnaire. The survey gathered information on household characteristics, output, input use and other related characteristics. As argued by Feder and Umali (Reference Feder and Umali1993), components of the agricultural package may complement each other, although some of them may be adopted independently. From the logic of Feder and Umali (Reference Feder and Umali1993), farmers who practised one or more of the main CA principles (minimum tillage, crop rotation and permanent crop cover) are termed adopters.
Because this study is focused on EE with respect to the use of N fertilizers, we employ the NITZ tool to examine the difference between total N in the system and total above-ground uptake as nitrogen surplus.
We account for heterogeneity in farm and household characteristics by including variables like gender, education and age of household head, access to extension and credit, soil quality and distance to market in the analysis of the determinants of TE and EE. We account for access to information from institutional sources using visits by extension agents (Krishnan and Patnam, Reference Krishnan and Patnam2014). The access to credit ranges from formal sources (like banks and micro-credit agencies) to informal ones (like money lenders, friends and family relations), and captures the extent to which farmers are liquidity constrained. The variable is measured as whether farmers obtained credit in the production season, and whether they tried to access more credit than they obtained. We consider farmers as liquidity-constrained if they either sought, and were unable to obtain credit, or obtained less than their requirement. Access to credit is expected to shift farmers' liquidity constraint outward and facilitate their timely procurement of inputs, thereby improving farm efficiency.
Heterogeneous environmental production conditions such as soil condition may influence the production process. Following Sherlund et al. (Reference Sherlund, Barrett and Adesina2002) we include soil quality and regional fixed effect dummies as proxies for environmental conditions. Available evidence suggests that the subjective reporting of soil condition by African farmers is quite accurate (for example, Suri, Reference Suri2011). Since dry season land preparation is considered a unique CA technology principle, and considered to influence input use and output, we include seasonal dummies for land preparation in the model (Haggblade and Tembo, Reference Haggblade and Tembo2003). We also include a variable on distance to the nearest market, measured as the distance to the nearest bigger village or town with a market for farm inputs and output. The definitions of the variables employed in the econometric estimation are presented in table 1.
Table 1. Descriptive statistics of conservation agriculture technology adopters and non-adopters

Notes: Coefficients followed by *** indicate significance at the 1% level.
5.1. Empirical strategy
A translog functional form is employed to estimate TE and EE.Footnote
12
To be able to directly interpret the coefficients of the first-order terms as elasticities at the sample mean, we start by employing the log input mean correction strategy (
![]() $\log X_{i}- \log {\bar X}\rpar $
, with
$\log X_{i}- \log {\bar X}\rpar $
, with
![]() ${\bar X}$
denoting mean of X (Coelli et al., Reference Coelli, Estache, Perelman and Trujillo2003). A multi-stage empirical estimation strategy is employed to account for sample selection and technology heterogeneity.
${\bar X}$
denoting mean of X (Coelli et al., Reference Coelli, Estache, Perelman and Trujillo2003). A multi-stage empirical estimation strategy is employed to account for sample selection and technology heterogeneity.
We start by estimating a Probit model using observable farm and household characteristics to generate adoption propensity scores. This facilitates matching of CA technology adopters and non-adopters to correct for observable selectivity bias. We employ the nearest neighbour and kernel matching algorithms.Footnote 13 . In the nearest neighbour case, a maximum of five matches per
adopter with maximum tolerance (caliper) of 0.01 is used. We also employed an Epanechnikov kernel matching with bandwidth of 0.05. By comparing the means, the nearest neighbour produced better matched samples; thus the analysis is based on the samples obtained from the nearest neighbour matching method. Out of the 407, the procedure yielded a total of 372 matched observations, comprising 202 adopters and 170 non-adopters.
Table 1 reports the means of the variables for unmatched and matched samples of CA technology adopters and non-adopters. In contrast to the significant differences in most of the variables in the unmatched samples, the estimates indicate that there are no significant differences between the means of observable characteristics of adopters and non-adopters after matching. Thus, the balancing condition of the covariates is fulfilled (Leuven and Sianesi, Reference Leuven and Sianesi2003). The region of common support (see figure A2 in the online appendix) indicating the area with positive density within d = 1 and d = 0 distributions is between 0.017 and 0.99. Based on the propensity scores, the Greene (Reference Greene2010) selectivity correction variable is then estimated and included in the stochastic frontier model.
The empirical specification of the translog function for the stochastic frontier TE for a particular technology is expressed as
 $$\eqalign{ln\; Y_{i} & =\alpha_{0}+\sum\limits_j {\alpha_{j}\ ln\; X} +\alpha _{e}\; ln\; E_{i}+0.5 \sum\limits_j \sum\limits_m {\alpha_{jm}\; ln\; X_{ij}\; ln\; X_{im}} \cr & \quad +\sum\limits_j {\alpha_{je}\; ln\; X_{ij}\; ln\; E_{i}} +0.5 \alpha_{ee}\lpar ln\; E_{i} \rpar ^{2}+v_{i}-u_{i}\comma \; } $$
$$\eqalign{ln\; Y_{i} & =\alpha_{0}+\sum\limits_j {\alpha_{j}\ ln\; X} +\alpha _{e}\; ln\; E_{i}+0.5 \sum\limits_j \sum\limits_m {\alpha_{jm}\; ln\; X_{ij}\; ln\; X_{im}} \cr & \quad +\sum\limits_j {\alpha_{je}\; ln\; X_{ij}\; ln\; E_{i}} +0.5 \alpha_{ee}\lpar ln\; E_{i} \rpar ^{2}+v_{i}-u_{i}\comma \; } $$
where ln denotes natural logarithm, Y
i
, is total output, and the independent variables X
i
denote vector of input quantities (including land, seed and N fertilizers) and E
i
is the quantity of environmentally detrimental input (nitrogen surplus), v
i
is the random term (white noise), and u
i
is the nonnegative systematic error term accounting for inefficiency. It is assumed that
![]() $\alpha_{jm} = \alpha_{mj}$
. To avoid potential multicollinearity in the model, and given that labour and capital inputs have zero nitrogen content to support the EE estimation, we follow previous studies on EE (for example, Coelli et al., Reference Coelli, Lauwers and Huylenbroeck2007; Nguyen et al., Reference Nguyen, Hoang and Seo2012), and limit the input variables to land, seeds, nitrogen in output and nitrogen surplus. Specifically, Coelli et al. (Reference Coelli, Lauwers and Huylenbroeck2007) demonstrate that the material balance analogy, which is the focus of our study, allows for the possibility of some inputs (or outputs) having zero amounts of the material of interest.
$\alpha_{jm} = \alpha_{mj}$
. To avoid potential multicollinearity in the model, and given that labour and capital inputs have zero nitrogen content to support the EE estimation, we follow previous studies on EE (for example, Coelli et al., Reference Coelli, Lauwers and Huylenbroeck2007; Nguyen et al., Reference Nguyen, Hoang and Seo2012), and limit the input variables to land, seeds, nitrogen in output and nitrogen surplus. Specifically, Coelli et al. (Reference Coelli, Lauwers and Huylenbroeck2007) demonstrate that the material balance analogy, which is the focus of our study, allows for the possibility of some inputs (or outputs) having zero amounts of the material of interest.
Various factors including farm household characteristics could be responsible for technical and environmental inefficiency. Wang and Schmidt (Reference Wang and Schmidt2002) demonstrate that in the stochastic frontier framework, a single-stage procedure is the appropriate approach to jointly estimate inefficiency and the determinants of inefficiency. The technical inefficiency and EE across farms is modelled as a linear function of the inefficiency term u i and of a set of covariates as
where z
i
is an m × 1 vector of exogenous variables that influence inefficiency, γ is an m × 1 vector of parameters and ω
i
is a random variable truncating the normal distribution with mean zero and variance, σ2 at point of truncation
![]() $z_{i}^{\prime}\gamma$
(Battese and Coelli, Reference Battese and Coelli1995).
$z_{i}^{\prime}\gamma$
(Battese and Coelli, Reference Battese and Coelli1995).
Unlike jointly estimating the determinants of TE with the deterministic component of the SPF, Reinhard et al. (Reference Reinhard, Lovell and Thijssen2002) indicate that the determinants of EE are not required to be jointly estimated with the production frontier. We therefore estimate the determinants of EE in a two-stage approach. In the first stage, EE is calculated from parameter estimates describing the structure of production technology at full efficiency. Since EE is calculated (as in equation (8)) without a predetermined distributional assumption as in the case of TE, this phenomenon does not violate the independently identically distributed assumption raised by Battese and Coelli (Reference Battese and Coelli1995). Hence, EE can be estimated by expressing the logarithm of the minimum feasible nitrogen surplus as a function of other covariates of equation (14) in the second stage.
The choice of an appropriate model for the second-stage regression to avoid misleading results is not trivial in empirical analysis (for example, Simar and Wilson, Reference Simar and Wilson2007; Ramalho et al., Reference Ramalho, Ramalho and Henriques2010)Footnote 14 . Because of the bounded nature of efficiency scores [0,1], linear specifications or Tobit models are used to relate inefficiency scores to exogenous factors in Reinhard et al.'s (2002) EE framework (for example, Reinhard et al., Reference Reinhard, Lovell and Thijssen2002; Kouser and Qaim, Reference Kouser and Qaim2015). As in linear Probit models, Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010) argue that linear specification of the second-stage regression may not be appropriate since it violates the conceptual requirement that the predicted values of efficiency scores lie within a range of 0 to 1. Moreover, the marginal effect in the second-stage regression of constant change in covariate over the entire range of efficiency scores is not compatible with the bounded nature of efficiency scores.
Simar and Wilson (Reference Simar and Wilson2007) and McDonald (Reference McDonald2009) indicate that, rather than considering the efficiency score as a censoring mechanism, as implied in a Tobit model, observed efficiency scores are products of the way the scores are defined. Furthermore, the Tobit model is originally devised for censored dependent variables that are by nature limited to the so-called ‘corner solution’ variables. Since efficiency scores do not generally take on values of 0, the Tobit model is not a plausible specification for conditional mean of a variable like second-stage regression for efficiency defined on the interval [0,1] (Ramalho et al., Reference Ramalho, Ramalho and Henriques2010). To avoid the problems associated with using linear and Tobit models for second-stage regressions, Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010) demonstrate that using fractional regression models (FRM) is the most natural way of modelling bounded, proportional variables like efficiency scores.
The FRM provides several alternative functional forms for dealing with the typical asymmetric nature of efficiency scores and can be estimated by the quasi-maximum likelihood approach. This does not require assumptions about the conditional distribution of efficiency scores or heteroscedasticity patterns. Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010) indicate that in the FRM framework a single model is employed to explain efficiency scores of all households, including those that are fully efficient. But where there is a relatively high proportion of fully efficient households, a two-sided model is employed to explain separately, first, why some firms are efficient while others are not, and then the relative efficiency of inefficient firms. We follow the approach by Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010) and treat efficiency scores as descriptive measures of the relative EE of the sampled households. We employ alternative models including FRM logit, Probit, log-logistic (loglog) and complementary log-logistic (cloglog) for the second-stage estimation, and then test for the appropriate functional form. This generalization contrasts with the studies by Hoff (Reference Hoff2007) and McDonald (Reference McDonald2009) who employed only a logit FRM.
6. Empirical results
6.1. Production frontier
Table 2 presents estimates of the deterministic component of six separate SPF models with columns (1) and (2) for pooled sample, (3) and (4) for adopters and (5) and (6) for non-adopters. The pooled sample case gives an indication of technology heterogeneity and includes technology and non-technology corrected models. The group sample estimates are comprised of with and without selectivity-corrected term models. While the non-selectivity corrected model accounts for only observable biases, the selectivity-corrected model corrects for both observable and unobservable biases. Before discussing the estimates, we first test for inefficiency and selectivity. The likelihood ratio (LR) test of the null hypothesis of no technical inefficiency effects, given the specifications of the SPF model, yields
![]() ${\bi \chi}^{2} = 3.05$
against a critical value of σ
u
= 0. Thus, the null hypothesis is rejected, suggesting that most of the farmers are producing below the production frontier.Footnote
15
${\bi \chi}^{2} = 3.05$
against a critical value of σ
u
= 0. Thus, the null hypothesis is rejected, suggesting that most of the farmers are producing below the production frontier.Footnote
15
Table 2. Translog estimates of conventional and selectivity-corrected stochastic production frontier for the matched sample

Notes: Coefficients followed by *, ** and *** indicate significance at the 10%, 5% and 1% levels, respectively.
In the selectivity-corrected model estimates, the coefficient for the selectivity term (ρ) for adopters and non-adopters is significant at the conventional level. This suggests that estimating the SPF model without accounting for selection bias in this study will lead to biased TE and EE scores (Bravo-Ureta et al., Reference Bravo-Ureta, Greene and Solis2012; Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015).
As indicated earlier, the reported coefficients of the first-order terms are elasticities. The reported partial elasticities for most of the variables in the selectivity-corrected models for adopters and non-adopters are lower compared to those of the conventional models, suggesting that sample selection bias tends to overestimate average partial elasticities (Villano et al., Reference Villano, Bravo-Ureta, Solis and Fleming2015). The first-order term estimates indicate positive and significant effects of land, seeds and nitrogen on maize output, fulfilling the regularity condition of monotonicity. These results are consistent with the MF estimates of Moreira and Bravo-Ureta, (Reference Moreira and Bravo-Ureta2010) for dairy farms in Argentina, Uruguay and Chile.
The coefficient for the nitrogen surplus variable is, however, negative and significantly different from zero. Cuesta et al. (Reference Cuesta, Lovell and Zofio2009) also report a negative coefficient for the first-order term of the environmental burden product (sulphur-oxide) for US electricity firms. The estimates of nitrogen in the output and nitrogen surplus are intuitive and have both economic and environmental interpretations. Specifically, while increasing levels of nitrogen uptake by the crop contribute to higher output (or economic returns) and lower environmental burden from nitrogen, increasing levels of nitrogen surplus tend to reduce economic returns and increase potential environmental burden from nitrogen.
In line with Battese et al. (Reference Battese, Rao and O'Donnell2004), the LR test of the null hypothesis of homogenous technology is calculated after estimating the stochastic frontier by pooling the data from both technologies. The LR statistic is 152.92 and significant at the 1 per cent level (using a chi-square distribution with 26 degrees of freedom). The null hypothesis of technology homogeneity is therefore rejected, supporting the use of the MF approach in the estimation of TE and EE.
6.2. Technical and environmental efficiency
To compute the MF estimates, we first estimate individual group frontiers, which are simulated to derive the MF estimates for the entire sample. Results for the group frontiers as well as parameter estimates for the MFs (quadratic programming) and the simulated standard errors are presented in table 3 Footnote 16 . The estimates for CA and non-CA technology adopters and the quadratic programing indicate that the coefficients of all the inputs significantly influence the level of output, hence the tendency to influence TE and EE. For instance, while higher levels of nitrogen utilized to produce output contribute to increased output and TE, higher levels of nitrogen surplus tend to reduce output and increase environmental inefficiency.
Table 3. Stochastic production frontier estimates

Notes: Coefficients followed by * ** and *** indicate significance at the 10%, 5% and 1% levels, respectively.
As indicated previously, the MF function is used in the estimation of meta-technology ratio, as well as TE and EE for CA and non-CA technologies. The parameters of the MF are used in the estimation of MTR and TE and EE. Table 4 reports a summary of TE and EE scores for the pooled, CA and non-CA technology group frontiers, respectively. The group-specific inefficiency scores relate to individual group frontiers with no common reference between groups. For a reasonable interpretation and comparison of the differences in efficiencies between CA and non-CA technology farms, we use the meta-technology ratio and MF scores.
Table 4. Meta-frontier technical and environmental efficiency estimates

Notes: Coefficients followed by *** indicate significance at the 1% level.
The estimates indicate statistically significant differences in the meta-technology ratio, TE and EE between CA and non-CA technology farms. The reported meta-technology ratios indicate the specific technology-related productivity gaps between CA and non-CA technologies relative to the MF, with a higher score indicating better returns from the technology. The results show an average meta-technology ratio score of about 0.94 for CA farms, ranging from 0.34 to 1.00. On the other hand, an average meta-technology ratio of 0.76 is reported for non-CA farms, ranging from 0.17 to 1.00.
The MF scores indicate that, on average, while CA technology farms are about 80 per cent technically efficient, their non-CA technology counterparts are 59 per cent technically efficient. These findings suggest that with the same level of inputs the CA technology tends to contribute to increasing average farm output by 19 per cent more than conventional farming. Similarly, while average EE for CA farms is about 52 per cent (48 per cent inefficient), average EE for non-CA farms is 32 per cent (68 per cent inefficient). This indicates that CA technology is more likely to contribute to reducing potential environmental degradation and GHG equivalent from nitrogen sources by 20 per cent more than non-CA technology farms. These differences can be attributed to better production technologies associated with CA technology, which includes incorporating fertilizers into the rip lines, minimum tillage and retention of crop cover to conserve soil and water, as well as reducing nitrogen losses resulting from volatilization, runoff and leaching.
As suggested by Wei et al. (Reference Wei, White, Hu and Willett2010), the estimates can be related to social cost in terms of equivalent impacts of a tonne of CO2 emission into the atmosphere. The relatively higher EE from CA compared to conventional technology indicates that CA technology tends to lower carbon dioxide and GHG emission equivalence from N fertilizers; hence CA technology will generate less social cost. Coupled with better TE, CA technology is likely to enhance the desired prosperity, people and planet synergies of the Sustainable Development Goals of agriculture (UN, 2015).
6.3. Determinants of technical and environmental efficiency
The determinants of efficiency indicate the potential sources of efficiency that could enhance policy, irrespective of technology. In table 5 we present translog maximum likelihood estimates of the determinants of technical inefficiency, as well as the FRM estimates of the determinants of environmental efficiency. The translog maximum likelihood frontier estimates are from a single-stage selectivity-corrected pooled sample SPF and inefficiency models. Given that there were no environmentally efficient households at unity in our sample, we use one-part models for our estimation of the determinants of EE. The results obtained for the one-part FRM for logit, Probit, loglog and cloglog follow the second-stage procedure of Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010)Footnote 17 .
Table 5. Determinants of efficiency Environmental efficiency (fractional regression model estimates for one-part models)

Notes: Coefficients followed by ** and *** indicate significance at the 5% and 1% levels, respectively.
For each FRM, we report the R 2 and test statistic. The R 2 is calculated as the square of the correlation between the actual and predicted efficiency scores. We find that most of the R 2 values are similar – evidence that all the competing models fit the data. Consistent with Ramalho et al. (Reference Ramalho, Ramalho and Henriques2010), the test statistic results clearly show that only the cloglog model is not rejected at the 10 per cent levelFootnote 18 . We therefore select the cloglog model as the most suitable model and for the interpretation of our results. The coefficients are interpreted by their signs, such that a positive (negative) coefficient for the technical inefficiency results indicates a positive (negative) effect on inefficiency, and the opposite for the EE determinants. In the interest of brevity, we only discuss the determinants focusing on variables that are statistically significant at conventional levelsFootnote 19 .
The inefficiency model estimates show that, while technical inefficiency is influenced by education, access to credit and distance to markets, EE appears to be influenced by age, education, access to extension, access to credit and distance to markets. The coefficient of the variable representing education in the TE (EE) model is negative (positive) and significantly different from zero, indicating that higher levels of education have the potential to reduce inefficiency. The result of the TE model is consistent with findings from other studies like Kibaara (Reference Kibaara2005) for Kenya, and Ng'ombe and Kalinda (Reference Ng'ombe and Kalinda2015) for Zambia.
The variable age is used as a proxy for experience of the farm household head, especially in the study area where farming is the main source of livelihood for most households. The estimate for age is positive and significantly different from zero for the EE model, suggesting that more experienced farmers are environmentally efficient. This is related to the fact that advancing years of farming experience improve farmers' ability to process relevant farm information for decision making. The results also reveal a negative (positive) and significant relationship between the variable representing access to credit and technical (environmental) inefficiency model, suggesting that liquidity-constrained farmers tend to be less efficient. This finding is in line with the results reported by Ng'ombe and Kalinda (Reference Ng'ombe and Kalinda2015), who showed that access to credit reduces farmers' cash constraints for farm input in Zambia, thereby increasing farm efficiency.
The access to extension variable also has positive relationship with EE, indicating the significance of information from extension services to improving EE. The reported positive (negative) and statistically significant relationship between the distance to market and technical (environmental) inefficiency suggests that farmers closer to markets tend to be more environmentally efficient. The reason for this could be linked to lower transaction cost in acquiring information from input markets on environmentally friendly inputs and acquiring the needed farm implements for soil and water conservation measures.
7. Conclusions
In this study, we examined EE among maize farmers in Zambia, with particular reference to N fertilizers. In generating a nitrogen balance sheet, we used a NITZ tool to establish that the quantity of applied N ferti-lizers is split into quantity of nitrogen that yielded the output and quantity of nitrogen surplus. We employed a MF approach to account for technology differences among farmers practising CA technology and those using conventional farming technology. We accounted for observable and unobservable selection bias, using PSM and Greene's (Reference Greene2010) sample selection SPF approach.
The empirical results revealed that CA technology farmers are technically and environmentally more efficient than conventional farming technology farmers, a finding that suggests that CA has the potential to reduce the economic drain and environmental burden that may arise from nitrogen surplus. The MF estimates also showed that CA technology farms are technically and environmentally more efficient than the non-CA technology farms. This demonstrates that CA technology has a potential to improve farm economic returns from farm output and reduce environmental burden from nitrogen losses. Less environmental burden from CA technology is an indication of less social cost from CA technology (Wei et al., Reference Wei, White, Hu and Willett2010).
The findings also established statistically significant differences in key determinants of TE and EE. In particular, we found positive and statistically significant relations between TE and access to credit, as well as education of the household head and shorter distance to markets. Similarly, EE was found to be positively related to access to credit, access to extension services, age, years of education and shorter distances to markets, indicating that there is scope for using policy measures to influence TE and EE.
In terms of policy, this study revealed that policy makers should continue with encouraging farm households to adopt CA technology, which has the potential to fulfil synergies between reducing social cost, enhancing economic empowerment and reducing environmental pollution. Specifically, encouraging soil and water conservation measures such as minimum tillage and retaining permanent crop cover would contribute to improving soil nutrients and water conservation. Also crop rotation, including the use of legumes in the rotation, could enhance nitrogen fixation, and timely land preparation would help to take advantage of nitrogen flush, hence improving output and reducing environmental pollution. Moreover, investment in rural infrastructure, including better roads and transport, will reduce farm transaction costs and improve the economic wellbeing of farmers. Improving farmers' access to timely credit packages, including cash and input credit, would also contribute to decreasing farm-level technical and environmental inefficiency.
Supplementary material and methods
To view supplementary material for this article, please visit https://doi.org/10.1017/S1355770X16000309.






