Article contents
Sobolev Estimation of Approximate Regressions
Published online by Cambridge University Press: 11 February 2009
Abstract
This paper focuses on the estimation of an approximated function and its derivatives. Let us assume that the data-generating process can be described by a family of regression models 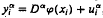 , where a is a multi-index of differentiation such that Dαϕ(xi) is the αth derivative of ϕ(xi) with respect to xi. The estimated model is characterized by a family Dαf(Xi|θ), where Dαf(Xi|θ) is the αth derivative of f(xi,|θ) and θ is an unknown parameter. The model is in general misspecified; that is, there is no θ such that Dαf(Xi|6) is equal to Dαϕ(Xi). Three different problems are discussed. First, the asymptotic behavior of the seemingly unrelated regression estimator of θ is shown to achieve the best approximation, in the Sobolev norm sense, of ϕ by an element of (f(Xi|θ)|θ ε Θ). Second, in the case of polynomial approximations, the expected derivatives of the limit of the estimated regression and of the true regression are proved to be equal if and only if the set of explanatory variables has a normal distribution. Third, different sets of α are introduced, and the different limits of estimated regressions characterized by these sets are proved to be equal if and only if the explanatory variables have a normal distribution. This result leads to a specification test.
, where a is a multi-index of differentiation such that Dαϕ(xi) is the αth derivative of ϕ(xi) with respect to xi. The estimated model is characterized by a family Dαf(Xi|θ), where Dαf(Xi|θ) is the αth derivative of f(xi,|θ) and θ is an unknown parameter. The model is in general misspecified; that is, there is no θ such that Dαf(Xi|6) is equal to Dαϕ(Xi). Three different problems are discussed. First, the asymptotic behavior of the seemingly unrelated regression estimator of θ is shown to achieve the best approximation, in the Sobolev norm sense, of ϕ by an element of (f(Xi|θ)|θ ε Θ). Second, in the case of polynomial approximations, the expected derivatives of the limit of the estimated regression and of the true regression are proved to be equal if and only if the set of explanatory variables has a normal distribution. Third, different sets of α are introduced, and the different limits of estimated regressions characterized by these sets are proved to be equal if and only if the explanatory variables have a normal distribution. This result leads to a specification test.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1996
References
REFERENCES
- 7
- Cited by

