Article contents
IDENTIFYING RESTRICTIONS FOR FINITE PARAMETER CONTINUOUS TIME MODELS WITH DISCRETE TIME DATA
Published online by Cambridge University Press: 22 December 2015
Abstract
This paper revisits the question of parameter identification when a linear continuous time model is sampled only at equispaced points in time. Following the framework and assumptions of Phillips (1973), we consider models characterized by first-order, linear systems of stochastic differential equations and use a priori restrictions on the model parameters as identifying restrictions. A practical rank condition is derived to test whether any particular collection of at least 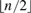 $\left\lfloor {n/2} \right\rfloor$ general linear restrictions on the parameter matrix is sufficient for identification. We then consider extensions to incorporate prior restrictions on the covariance matrix of the disturbances, to identify the covariance matrix itself, and to address identification in models with cointegration.
$\left\lfloor {n/2} \right\rfloor$ general linear restrictions on the parameter matrix is sufficient for identification. We then consider extensions to incorporate prior restrictions on the covariance matrix of the disturbances, to identify the covariance matrix itself, and to address identification in models with cointegration.
Information
- Type
- MISCELLANEA
- Information
- Copyright
- Copyright © Cambridge University Press 2015
Footnotes
I am grateful to John Geweke, Robert de Jong, Matt Masten, Tucker McElroy, Peter Phillips, and three anonymous referees for useful comments and discussions.
References
REFERENCES
- 9
- Cited by

