Article contents
IDENTIFICATION AND ESTIMATION IN A CORRELATED RANDOM COEFFICIENTS TRANSFORMATION MODEL
Published online by Cambridge University Press: 04 June 2021
Abstract
This study examines identification and estimation in a correlated random coefficients (CRC) model with an unknown transformation of the dependent variable, namely 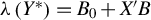 $\lambda \left (Y^{*}\right)=B_{0}+X^{\prime }B$, where the latent outcome
$\lambda \left (Y^{*}\right)=B_{0}+X^{\prime }B$, where the latent outcome 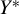 $Y^{*}$ may be subject to a certain kind of censoring mechanism,
$Y^{*}$ may be subject to a certain kind of censoring mechanism, 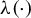 $\lambda (\cdot)$ is an unknown, one-to-one monotone function, and the random coefficients
$\lambda (\cdot)$ is an unknown, one-to-one monotone function, and the random coefficients 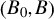 $\left (B_{0},B\right)$ are allowed to be correlated with one or several components of X. Under a conditional median independence plus a conditional median zero restriction, the mean of B is shown to be identified up to scale. Moreover, we show the derivative of the median structural function (MSF) is point identified. This derivative of MSF resembles the marginal treatment effect introduced by Heckman and Vytlacil (2005, Econometrica 73, 669–738).
$\left (B_{0},B\right)$ are allowed to be correlated with one or several components of X. Under a conditional median independence plus a conditional median zero restriction, the mean of B is shown to be identified up to scale. Moreover, we show the derivative of the median structural function (MSF) is point identified. This derivative of MSF resembles the marginal treatment effect introduced by Heckman and Vytlacil (2005, Econometrica 73, 669–738).
It generalizes the usual average treatment effect in a linear CRC model and coincides with 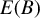 $E(B)$ when
$E(B)$ when 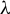 $\lambda $ is equal to the identity function; it is invariant to both location and scale normalization on the coefficients. We develop estimators for the identified parameters and derive asymptotic properties for the derivative of MSF. An empirical example using the U.K. Family Expenditure Survey is provided.
$\lambda $ is equal to the identity function; it is invariant to both location and scale normalization on the coefficients. We develop estimators for the identified parameters and derive asymptotic properties for the derivative of MSF. An empirical example using the U.K. Family Expenditure Survey is provided.
Information
- Type
- ARTICLES
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
We are grateful to the editor Peter C.B. Phillips, the co-editor Arthur Lewbel, and four anonymous referees for their insightful comments. This research is supported by the National Science Foundation of China (71873080), the Key Project of the National Science Foundation of China (71833004), the Fundamental Research Funds for the Central Universities (2021110070), and the 2018 Program for Innovative Research Team of the Shanghai University of Finance and Economics.
References
REFERENCES
- 2
- Cited by

