Article contents
ESTIMATION OF THE KRONECKER COVARIANCE MODEL BY QUADRATIC FORM
Published online by Cambridge University Press: 17 December 2020
Abstract
We propose a new estimator, the quadratic form estimator, of the Kronecker product model for covariance matrices. We show that this estimator has good properties in the large dimensional case (i.e., the cross-sectional dimension n is large relative to the sample size T). In particular, the quadratic form estimator is consistent in a relative Frobenius norm sense provided 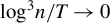 ${\log }^3n/T\to 0$. We obtain the limiting distributions of the Lagrange multiplier and Wald tests under both the null and local alternatives concerning the mean vector
${\log }^3n/T\to 0$. We obtain the limiting distributions of the Lagrange multiplier and Wald tests under both the null and local alternatives concerning the mean vector 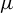 $\mu $. Testing linear restrictions of
$\mu $. Testing linear restrictions of 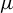 $\mu $ is also investigated. Finally, our methodology is shown to perform well in finite sample situations both when the Kronecker product model is true and when it is not true.
$\mu $ is also investigated. Finally, our methodology is shown to perform well in finite sample situations both when the Kronecker product model is true and when it is not true.
Information
- Type
- ARTICLES
- Information
- Econometric Theory , Volume 38 , Issue 5: YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS: PART I , October 2022 , pp. 1014 - 1067
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
We thank the Editor Peter C.B. Phillips, the Co-Editor Yuichi Kitamura, and two anonymous referees for detailed comments, which greatly improved the article. For useful discussions, we are grateful to Liang Jiang, Chen Wang, Tengyao Wang, and the participants at the Celebration of Peter C.B. Phillips’ Forty Years at Yale held at Yale University on October 19-20, 2018 and the CUHK Workshop on Econometrics 2019. Any remaining errors are our own. Oliver B. Linton thanks the Cambridge INET and the Keynes Fund for financial support. Haihan Tang is sponsored by the National Natural Science Foundation of China (grant number 71903034) and Shanghai Pujiang Program (grant number 2019PJC015).
References
REFERENCES
- 1
- Cited by

