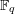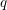Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bernasconi, Fabio
and
Tanaka, Hiromu
2022.
ON DEL PEZZO FIBRATIONS IN POSITIVE CHARACTERISTIC.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 1,
p.
197.
Hacon, Christopher
and
Witaszek, Jakub
2023.
On the relative minimal model program for fourfolds in positive and mixed characteristic.
Forum of Mathematics, Pi,
Vol. 11,
Issue. ,
Bernasconi, Fabio
and
Kollár, János
2023.
Vanishing Theorems for Three-folds in Characteristicp> 5.
International Mathematics Research Notices,
Vol. 2023,
Issue. 4,
p.
2846.
Filipazzi, Stefano
and
Waldron, Joe
2024.
Connectedness Principle for 3-Folds in Characteristic p>5.
Michigan Mathematical Journal,
Vol. 74,
Issue. 4,
Xie, Lingyao
and
Xue, Qingyuan
2024.
On the Termination of the MMP for Semistable Fourfolds in Mixed Characteristic.
Michigan Mathematical Journal,
Vol. 74,
Issue. 5,
Bernasconi, Fabio
and
Filipazzi, Stefano
2025.
Rational points on 3‐folds with nef anti‐canonical class over finite fields.
Proceedings of the London Mathematical Society,
Vol. 130,
Issue. 1,