Article contents
Universal polynomials for singular curves on surfaces
Published online by Cambridge University Press: 06 June 2014
Abstract
Let 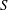 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ be a complex smooth projective surface and
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ be a complex smooth projective surface and 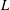 $L$ be a line bundle on
$L$ be a line bundle on 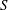 $S$. For any given collection of isolated topological or analytic singularity types, we show the number of curves in the linear system
$S$. For any given collection of isolated topological or analytic singularity types, we show the number of curves in the linear system 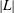 $|L|$ with prescribed singularities is a universal polynomial of Chern numbers of
$|L|$ with prescribed singularities is a universal polynomial of Chern numbers of 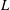 $L$ and
$L$ and 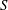 $S$, assuming
$S$, assuming 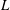 $L$ is sufficiently ample. More generally, we show for vector bundles of any rank and smooth varieties of any dimension, similar universal polynomials also exist and equal the number of singular subvarieties cutting out by sections of the vector bundle. This work is a generalization of Göttsche’s conjecture.
$L$ is sufficiently ample. More generally, we show for vector bundles of any rank and smooth varieties of any dimension, similar universal polynomials also exist and equal the number of singular subvarieties cutting out by sections of the vector bundle. This work is a generalization of Göttsche’s conjecture.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 8
- Cited by

