Article contents
Topological Fukaya category and mirror symmetry for punctured surfaces
Published online by Cambridge University Press: 14 March 2019
Abstract
In this paper we establish a version of homological mirror symmetry for punctured Riemann surfaces. Following a proposal of Kontsevich we model A-branes on a punctured surface 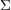 $\unicode[STIX]{x1D6F4}$ via the topological Fukaya category. We prove that the topological Fukaya category of
$\unicode[STIX]{x1D6F4}$ via the topological Fukaya category. We prove that the topological Fukaya category of  $\unicode[STIX]{x1D6F4}$ is equivalent to the category of matrix factorizations of a certain mirror LG model
$\unicode[STIX]{x1D6F4}$ is equivalent to the category of matrix factorizations of a certain mirror LG model 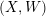 $(X,W)$. Along the way we establish new gluing results for the topological Fukaya category of punctured surfaces which are of independent interest.
$(X,W)$. Along the way we establish new gluing results for the topological Fukaya category of punctured surfaces which are of independent interest.
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
Current address: School of Mathematics, Statistics and Actuarial Science (SMSAS), University of Kent, Sibson Building, Parkwood Road, Canterbury, CT2 7FS, UKemail N.Sibilla@kent.ac.uk
References
- 6
- Cited by

