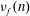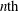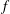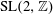Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fouvry, Étienne
Kowalski, Emmanuel
and
Michel, Philippe
2015.
Algebraic twists of modular forms and Hecke orbits.
Geometric and Functional Analysis,
Vol. 25,
Issue. 2,
p.
580.
Hou, Fei
2015.
Oscillations of coefficients of symmetric square L-functions over primes.
Frontiers of Mathematics in China,
Vol. 10,
Issue. 6,
p.
1325.
Hou, Fei
and
Lü, Guangshi
2016.
Oscillations of Fourier coefficients of cusp forms over primes.
Journal of Number Theory,
Vol. 159,
Issue. ,
p.
370.
Hou, Fei
2016.
On exponential sums involving Fourier coefficients of cusp forms over primes.
Journal of Number Theory,
Vol. 164,
Issue. ,
p.
375.
Hou, Fei
Jiang, Yujiao
and
Lü, Guangshi
2016.
ON EXPONENTIAL SUMS INVOLVING COEFFICIENTS OFL-FUNCTIONS FOR SL(3, ℤ) OVER PRIMES.
The Quarterly Journal of Mathematics,
Vol. 67,
Issue. 2,
p.
285.
Zaghloul, Giamila
2016.
Quadratic forms connected with Fourier coefficients of holomorphic and Maass cusp forms.
Journal of Number Theory,
Vol. 167,
Issue. ,
p.
118.
Jiang, Yujiao
and
Lü, Guangshi
2017.
Exponential sums formed with the von Mangoldt function and Fourier coefficients of $${ GL}(m)$$ G L ( m ) automorphic forms.
Monatshefte für Mathematik,
Vol. 184,
Issue. 4,
p.
539.
Acharya, Ratnadeep
2018.
An analogue of the Bombieri–Vinogradov Theorem for Fourier coefficients of cusp forms.
Mathematische Zeitschrift,
Vol. 288,
Issue. 1-2,
p.
23.
Acharya, Ratnadeep
2019.
Strong orthogonality between the Möbius function, additive characters and the coefficients of the L-functions of degree three.
Journal of Number Theory,
Vol. 203,
Issue. ,
p.
211.
Miller, Stephen D
and
Zhou, Fan
2019.
The Balanced Voronoi Formulas for $\textrm{GL}(n)$.
International Mathematics Research Notices,
Vol. 2019,
Issue. 11,
p.
3473.
Jiang, Yujiao
and
Lü, Guangshi
2019.
On automorphic analogues of the Möbius randomness principle.
Journal of Number Theory,
Vol. 197,
Issue. ,
p.
268.
Lü, Guangshi
and
Xi, Ping
2019.
On triple correlations of Fourier coefficients of cusp forms. II.
International Journal of Number Theory,
Vol. 15,
Issue. 04,
p.
713.
El Abdalaoui, El Houcein
and
Shparlinski, Igor E.
2019.
Disjointness of the Möbius Transformation and Möbius Function.
Research in the Mathematical Sciences,
Vol. 6,
Issue. 1,
Cafferata, M
Perelli, A
and
Zaccagnini, A
2020.
AN EXTENSION OF THE BOURGAIN–SARNAK–ZIEGLER THEOREM WITH MODULAR APPLICATIONS.
The Quarterly Journal of Mathematics,
Vol. 71,
Issue. 1,
p.
359.
Jiang, Yujiao
and
Lü, Guangshi
2020.
On an analogue of prime vectors among integer lattice points in ellipsoids for automorphic forms.
International Journal of Number Theory,
Vol. 16,
Issue. 01,
p.
145.
Acharya, Ratnadeep
2020.
Exponential sums of squares of Fourier coefficients of cusp forms.
Proceedings - Mathematical Sciences,
Vol. 130,
Issue. 1,
Jiang, Yujiao
and
Lü, Guangshi
2020.
The Bombieri–Vinogradov Theorem on Higher Rank Groups and its Applications.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 4,
p.
928.
Acharya, Ratnadeep
and
Singh, Saurabh Kumar
2021.
An exponential sum involving Fourier coefficients of eigenforms for $$SL(2,\pmb {{\mathbb {Z}}})$$.
The Ramanujan Journal,
Vol. 54,
Issue. 3,
p.
699.
Jiang, Yujiao
and
Lü, Guangshi
2021.
The generalized Bourgain-Sarnak-Ziegler criterion and its application to additively twisted sums on GLm.
Science China Mathematics,
Vol. 64,
Issue. 10,
p.
2207.
Jiang, Yujiao
Lü, Guangshi
and
Wang, Zihao
2022.
Möbius randomness law for 𝐺𝐿(𝑚) automorphic 𝐿-functions twisted by additive characters.
Proceedings of the American Mathematical Society,
Vol. 151,
Issue. 2,
p.
475.