Article contents
Stability of products of equivalence relations
Published online by Cambridge University Press: 17 August 2018
Abstract
An ergodic probability measure preserving (p.m.p.) equivalence relation 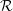 ${\mathcal{R}}$ is said to be stable if
${\mathcal{R}}$ is said to be stable if 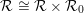 ${\mathcal{R}}\cong {\mathcal{R}}\times {\mathcal{R}}_{0}$ where
${\mathcal{R}}\cong {\mathcal{R}}\times {\mathcal{R}}_{0}$ where 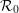 ${\mathcal{R}}_{0}$ is the unique hyperfinite ergodic type
${\mathcal{R}}_{0}$ is the unique hyperfinite ergodic type 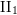 $\text{II}_{1}$ equivalence relation. We prove that a direct product
$\text{II}_{1}$ equivalence relation. We prove that a direct product 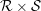 ${\mathcal{R}}\times {\mathcal{S}}$ of two ergodic p.m.p. equivalence relations is stable if and only if one of the two components
${\mathcal{R}}\times {\mathcal{S}}$ of two ergodic p.m.p. equivalence relations is stable if and only if one of the two components 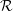 ${\mathcal{R}}$ or
${\mathcal{R}}$ or 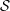 ${\mathcal{S}}$ is stable. This result is deduced from a new local characterization of stable equivalence relations. The similar question on McDuff
${\mathcal{S}}$ is stable. This result is deduced from a new local characterization of stable equivalence relations. The similar question on McDuff 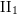 $\text{II}_{1}$ factors is also discussed and some partial results are given.
$\text{II}_{1}$ factors is also discussed and some partial results are given.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2018
Footnotes
The author is supported by ERC Starting Grant GAN 637601.
References
- 6
- Cited by

