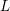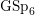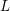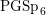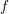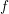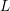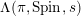Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gan, Wee Teck
and
Savin, Gordan
2020.
An exceptional Siegel–Weil formula and poles of the Spin L-function of.
Compositio Mathematica,
Vol. 156,
Issue. 6,
p.
1231.
Pollack, Aaron
2020.
The Fourier expansion of modular forms on quaternionic exceptional groups.
Duke Mathematical Journal,
Vol. 169,
Issue. 7,
Pollack, Aaron
2021.
Relative Trace Formulas.
p.
379.
Pollack, Aaron
Wan, Chen
and
Zydor, Michał
2021.
On the residue method for period integrals.
Duke Mathematical Journal,
Vol. 170,
Issue. 7,
Böcherer, Siegfried
and
Das, Soumya
2022.
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 6,
p.
2001.