Article contents
Sheaf quantization of Legendrian isotopy
Published online by Cambridge University Press: 17 February 2023
Abstract
Let 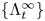 $\{\Lambda ^\infty _t\}$ be an isotopy of Legendrians (possibly singular) in a unit cosphere bundle
$\{\Lambda ^\infty _t\}$ be an isotopy of Legendrians (possibly singular) in a unit cosphere bundle 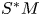 $S^*M$ that arise as slices of a singular Legendrian
$S^*M$ that arise as slices of a singular Legendrian 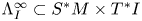 $\Lambda _I^\infty \subset S^*M \times T^*I$. Let
$\Lambda _I^\infty \subset S^*M \times T^*I$. Let 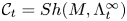 $\mathcal {C}_t = Sh(M, \Lambda ^\infty _t)$ be the differential graded derived category of constructible sheaves on
$\mathcal {C}_t = Sh(M, \Lambda ^\infty _t)$ be the differential graded derived category of constructible sheaves on 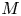 $M$ with singular support at infinity contained in
$M$ with singular support at infinity contained in 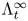 $\Lambda ^\infty _t$. We prove that if the isotopy of Legendrians embeds into an isotopy of Liouville hypersurfaces, then the family of categories
$\Lambda ^\infty _t$. We prove that if the isotopy of Legendrians embeds into an isotopy of Liouville hypersurfaces, then the family of categories 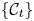 $\{\mathcal {C}_t\}$ is constant in
$\{\mathcal {C}_t\}$ is constant in 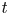 $t$.
$t$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
This work was supported by an IHES Simons Postdoctoral Fellowship as part of the Simons Collaboration on HMS.
In memory of Steve
References
- 2
- Cited by


