Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gee, Toby
2011.
On the weights of mod p Hilbert modular forms.
Inventiones mathematicae,
Vol. 184,
Issue. 1,
p.
1.
Emerton, Matthew
Gee, Toby
and
Herzig, Florian
2013.
Weight cycling and Serre-type conjectures for unitary groups.
Duke Mathematical Journal,
Vol. 162,
Issue. 9,
Diamond, Fred
and
Savitt, David
2015.
SERRE WEIGHTS FOR LOCALLY REDUCIBLE TWO-DIMENSIONAL GALOIS REPRESENTATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 14,
Issue. 3,
p.
639.
Gee, Toby
and
Geraghty, David
2015.
The Breuil–Mézard Conjecture for quaternion algebras.
Annales de l'Institut Fourier,
Vol. 65,
Issue. 4,
p.
1557.
Rozensztajn, Sandra
2015.
Potentially semi-stable deformation rings for discrete series extended types.
Journal de l’École polytechnique — Mathématiques,
Vol. 2,
Issue. ,
p.
179.
Chojecki, Przemysław
2015.
On non-abelian Lubin–Tate theory for .
Compositio Mathematica,
Vol. 151,
Issue. 8,
p.
1433.
Le, Daniel
Morra, Stefano
and
Park, Chol
2018.
On mod p local-global compatibility for GL3(Qp) in the non-ordinary case.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 4,
p.
790.
Park, Chol
2021.
A classification of Breuil modules.
Israel Journal of Mathematics,
Vol. 242,
Issue. 2,
p.
605.
Hu, Yongquan
and
Wang, Haoran
2024.
On some mod p representations of quaternion algebra over ℚp.
Compositio Mathematica,
Vol. 160,
Issue. 11,
p.
2585.

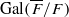 which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre
which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre 