Article contents
Self-dual integral normal bases and Galois module structure
Published online by Cambridge University Press: 10 May 2013
Abstract
Let 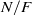 $N/ F$ be an odd-degree Galois extension of number fields with Galois group
$N/ F$ be an odd-degree Galois extension of number fields with Galois group 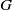 $G$ and rings of integers
$G$ and rings of integers 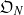 ${\mathfrak{O}}_{N} $ and
${\mathfrak{O}}_{N} $ and 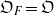 ${\mathfrak{O}}_{F} = \mathfrak{O}$. Let
${\mathfrak{O}}_{F} = \mathfrak{O}$. Let 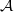 $ \mathcal{A} $ be the unique fractional
$ \mathcal{A} $ be the unique fractional 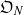 ${\mathfrak{O}}_{N} $-ideal with square equal to the inverse different of
${\mathfrak{O}}_{N} $-ideal with square equal to the inverse different of 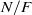 $N/ F$. B. Erez showed that
$N/ F$. B. Erez showed that 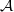 $ \mathcal{A} $ is a locally free
$ \mathcal{A} $ is a locally free 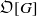 $\mathfrak{O}[G] $-module if and only if
$\mathfrak{O}[G] $-module if and only if 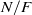 $N/ F$ is a so-called weakly ramified extension. Although a number of results have been proved regarding the freeness of
$N/ F$ is a so-called weakly ramified extension. Although a number of results have been proved regarding the freeness of 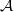 $ \mathcal{A} $ as a
$ \mathcal{A} $ as a 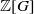 $ \mathbb{Z} [G] $-module, the question remains open. In this paper we prove that
$ \mathbb{Z} [G] $-module, the question remains open. In this paper we prove that 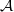 $ \mathcal{A} $ is free as a
$ \mathcal{A} $ is free as a 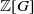 $ \mathbb{Z} [G] $-module provided that
$ \mathbb{Z} [G] $-module provided that 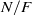 $N/ F$ is weakly ramified and under the hypothesis that for every prime
$N/ F$ is weakly ramified and under the hypothesis that for every prime 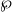 $\wp $ of
$\wp $ of 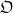 $\mathfrak{O}$ which ramifies wildly in
$\mathfrak{O}$ which ramifies wildly in 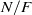 $N/ F$, the decomposition group is abelian, the ramification group is cyclic and
$N/ F$, the decomposition group is abelian, the ramification group is cyclic and 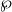 $\wp $ is unramified in
$\wp $ is unramified in 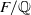 $F/ \mathbb{Q} $. We make crucial use of a construction due to the first author which uses Dwork’s exponential power series to describe self-dual integral normal bases in Lubin–Tate extensions of local fields. This yields a new and striking relationship between the local norm-resolvent and the Galois Gauss sum involved. Our results generalise work of the second author concerning the case of base field
$F/ \mathbb{Q} $. We make crucial use of a construction due to the first author which uses Dwork’s exponential power series to describe self-dual integral normal bases in Lubin–Tate extensions of local fields. This yields a new and striking relationship between the local norm-resolvent and the Galois Gauss sum involved. Our results generalise work of the second author concerning the case of base field 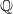 $ \mathbb{Q} $.
$ \mathbb{Q} $.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013
References
- 6
- Cited by

