Article contents
Robinson’s conjecture on heights of characters
Published online by Cambridge University Press: 20 May 2019
Abstract
Geoffrey Robinson conjectured in 1996 that the 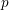 $p$-part of character degrees in a
$p$-part of character degrees in a 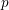 $p$-block of a finite group can be bounded in terms of the center of a defect group of the block. We prove this conjecture for all primes
$p$-block of a finite group can be bounded in terms of the center of a defect group of the block. We prove this conjecture for all primes 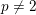 $p\neq 2$ for all finite groups. Our argument relies on a reduction by Murai to the case of quasi-simple groups which are then studied using deep results on blocks of finite reductive groups.
$p\neq 2$ for all finite groups. Our argument relies on a reduction by Murai to the case of quasi-simple groups which are then studied using deep results on blocks of finite reductive groups.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
The first and fourth authors gratefully acknowledge financial support by SFB TRR 195, and the others by NSFC (No. 11631001). In addition, the third author gratefully acknowledges financial support by NSFC (No. 11661042) and the Key Laboratory of Mathematics and Its Applications of Peking University.
References
- 8
- Cited by

