Article contents
Rigidity of the mod 2 families Seiberg–Witten invariants and topology of families of spin 4-manifolds
Part of:
Differential topology
Published online by Cambridge University Press: 15 April 2021
Abstract
We show a rigidity theorem for the Seiberg–Witten invariants mod 2 for families of spin 4-manifolds. A mechanism of this rigidity theorem also gives a family version of 10/8-type inequality. As an application, we prove the existence of non-smoothable topological families of 4-manifolds whose fiber, base space, and total space are smoothable as manifolds. These non-smoothable topological families provide new examples of 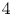 $4$-manifolds
$4$-manifolds 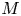 $M$ for which the inclusion maps
$M$ for which the inclusion maps 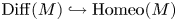 $\operatorname {Diff}(M) \hookrightarrow \operatorname {Homeo}(M)$ are not weak homotopy equivalences. We shall also give a new series of non-smoothable topological actions on some spin
$\operatorname {Diff}(M) \hookrightarrow \operatorname {Homeo}(M)$ are not weak homotopy equivalences. We shall also give a new series of non-smoothable topological actions on some spin 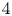 $4$-manifolds.
$4$-manifolds.
MSC classification
Secondary:
57R50: Diffeomorphisms
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
References
Atiyah, M. F. and Singer, I. M., The index of elliptic operators. IV, Ann. of Math. (2) 93 (1971), 119–138; MR279833.CrossRefGoogle Scholar
Baraglia, D., Obstructions to smooth group actions on 4-manifolds from families Seiberg-Witten theory, Adv. Math. 354 (2019), 106730; MR3981995.CrossRefGoogle Scholar
Baraglia, D., Constraints on families of smooth 4-manifolds from Bauer-Furuta invariants, Preprint (2019), arXiv:1907.03949.Google Scholar
Baraglia, D. and Konno, H., On the Bauer-Furuta and Seiberg-Witten invariants of families of 4-manifolds, Preprint (2019), arXiv:1903.01649.Google Scholar
Baraglia, D. and Konno, H., A gluing formula for families Seiberg–Witten invariants, Geom. Topol. 24 (2020), 1381–1456; MR4157556.CrossRefGoogle Scholar
Bauer, S., Almost complex  $4$-manifolds with vanishing first Chern class, J. Differential Geom. 79 (2008), 25–32; MR2414748.CrossRefGoogle Scholar
$4$-manifolds with vanishing first Chern class, J. Differential Geom. 79 (2008), 25–32; MR2414748.CrossRefGoogle Scholar
Bauer, S. and Furuta, M., A stable cohomotopy refinement of Seiberg-Witten invariants. I, Invent. Math. 155 (2004), 1–19; MR2025298.CrossRefGoogle Scholar
Boardman, J. M. and Vogt, R. M., Homotopy-everything  $H$-spaces, Bull. Amer. Math. Soc. 74 (1968), 1117–1122; MR0236922.CrossRefGoogle Scholar
$H$-spaces, Bull. Amer. Math. Soc. 74 (1968), 1117–1122; MR0236922.CrossRefGoogle Scholar
Donaldson, S. K., Polynomial invariants for smooth four-manifolds, Topology 29 (1990), 257–315; MR1066174.CrossRefGoogle Scholar
Donaldson, S. K., Floer homology groups in Yang-Mills theory, Cambridge Tracts in Mathematics, vol. 147 (Cambridge University Press, Cambridge, 2002), with the assistance of M. Furuta and D. Kotschick; MR1883043.CrossRefGoogle Scholar
Farb, B. and Margalit, D., A primer on mapping class groups, Princeton Mathematical Series, vol. 49 (Princeton University Press, Princeton, NJ, 2012); MR2850125.Google Scholar
Freedman, M. H., The topology of four-dimensional manifolds, J. Differential Geometry 17 (1982), 357–453; MR679066.CrossRefGoogle Scholar
Freedman, M.H. and Quinn, F., Topology of 4-manifolds, Princeton Mathematical Series, vol. 39 (Princeton University Press, Princeton, NJ, 1990); MR1201584.Google Scholar
Furuta, M., Stable homotopy version of Seiberg-Witten invariant, Preprint.Google Scholar
Furuta, M., Monopole equation and the  $\frac {11}8$-conjecture, Math. Res. Lett. 8 (2001), 279–291; MR1839478.CrossRefGoogle Scholar
$\frac {11}8$-conjecture, Math. Res. Lett. 8 (2001), 279–291; MR1839478.CrossRefGoogle Scholar
Furuta, M. and Kametani, Y., Equivariant maps between sphere bundles over tori and KO-degree, Preprint (2005), arXiv:math/0502511.Google Scholar
Furuta, M., Kametani, Y. and Matsue, H., Spin  $4$-manifolds with signature
$4$-manifolds with signature  $=-32$, Math. Res. Lett. 8 (2001), 293–301; MR1839479.CrossRefGoogle Scholar
$=-32$, Math. Res. Lett. 8 (2001), 293–301; MR1839479.CrossRefGoogle Scholar
Hatcher, A. E., Linearization in 3-dimensional topology, in Proceedings of the International Congress of Mathematicians (Helsinki, 1978) (Acad. Sci. Fennica, Helsinki, 1980), 463–468; MR562642.Google Scholar
Kato, Y., Nonsmoothable actions of  ${\Bbb Z}_2 \times {\Bbb Z}_2$ on spin four-manifolds, Preprint (2017), arXiv:1708.08030.Google Scholar
${\Bbb Z}_2 \times {\Bbb Z}_2$ on spin four-manifolds, Preprint (2017), arXiv:1708.08030.Google Scholar
Kirby, R.C. and Siebenmann, L.C., Foundational essays on topological manifolds, smoothings, and triangulations, Annals of Mathematics Studies, vol. 88 (Princeton University Press, Princeton, NJ, 1977), with notes by J. Milnor and M. Atiyah; MR0645390.CrossRefGoogle Scholar
Kister, J. M., Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199; MR0180986.CrossRefGoogle Scholar
Kuiper, N. H., The homotopy type of the unitary group of Hilbert space, Topology 3 (1965), 19–30; MR0179792.CrossRefGoogle Scholar
Li, T.-J., Symplectic  $4$-manifolds with Kodaira dimension zero, J. Differential Geom. 74 (2006), 321–352; MR2259057.CrossRefGoogle Scholar
$4$-manifolds with Kodaira dimension zero, J. Differential Geom. 74 (2006), 321–352; MR2259057.CrossRefGoogle Scholar
Li, T.-J., Quaternionic bundles and Betti numbers of symplectic  $4$-manifolds with Kodaira dimension zero, Int. Math. Res. Not. IMRN 2006 (2006), Art. ID 37385; MR2264722.CrossRefGoogle Scholar
$4$-manifolds with Kodaira dimension zero, Int. Math. Res. Not. IMRN 2006 (2006), Art. ID 37385; MR2264722.CrossRefGoogle Scholar
Li, T.-J. and Liu, A.-K., Family Seiberg–Witten invariants and wall crossing formulas, Comm. Anal. Geom. 9 (2001), 777–823; MR1868921 (2002k:57074).CrossRefGoogle Scholar
May, J. P. and Ponto, K., More concise algebraic topology: localization, completion, and model categories, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, 2012); MR2884233.Google Scholar
Morgan, J. W., The Seiberg-Witten equations and applications to the topology of smooth four-manifolds, Mathematical Notes, vol. 44 (Princeton University Press, Princeton, NJ, 1996); MR1367507.Google Scholar
Morgan, J. W. and Szabó, Z., Homotopy  $K3$ surfaces and mod
$K3$ surfaces and mod  $2$ Seiberg-Witten invariants, Math. Res. Lett. 4 (1997), 17–21; MR1432806.CrossRefGoogle Scholar
$2$ Seiberg-Witten invariants, Math. Res. Lett. 4 (1997), 17–21; MR1432806.CrossRefGoogle Scholar
Müller, C. and Wockel, C., Equivalences of smooth and continuous principal bundles with infinite-dimensional structure group, Adv. Geom. 9 (2009), 605–626; MR2574141.CrossRefGoogle Scholar
Nakamura, N., Smoothability of  $\Bbb Z\times \Bbb Z$-actions on
$\Bbb Z\times \Bbb Z$-actions on  $4$-manifolds, Proc. Amer. Math. Soc. 138 (2010), 2973–2978; MR2644908.CrossRefGoogle Scholar
$4$-manifolds, Proc. Amer. Math. Soc. 138 (2010), 2973–2978; MR2644908.CrossRefGoogle Scholar
Nicolaescu, L.I., Notes on Seiberg-Witten theory, Graduate Studies in Mathematics, vol. 28 (American Mathematical Society, Providence, RI, 2000); MR1787219.Google Scholar
Park, B. D. and Szabó, Z., The geography problem for irreducible spin four-manifolds, Trans. Amer. Math. Soc. 352 (2000), 3639–3650; MR1653371.CrossRefGoogle Scholar
Quinn, F., Ends of maps. III. Dimensions  $4$ and
$4$ and  $5$, J. Differential Geom. 17 (1982), 503–521; MR679069.CrossRefGoogle Scholar
$5$, J. Differential Geom. 17 (1982), 503–521; MR679069.CrossRefGoogle Scholar
Quinn, F., Isotopy of  $4$-manifolds, J. Differential Geom. 24 (1986), 343–372; MR868975.CrossRefGoogle Scholar
$4$-manifolds, J. Differential Geom. 24 (1986), 343–372; MR868975.CrossRefGoogle Scholar
Ruberman, D., An obstruction to smooth isotopy in dimension  $4$, Math. Res. Lett. 5 (1998), 743–758; MR1671187 (2000c:57061).CrossRefGoogle Scholar
$4$, Math. Res. Lett. 5 (1998), 743–758; MR1671187 (2000c:57061).CrossRefGoogle Scholar
Ruberman, D., A polynomial invariant of diffeomorphisms of 4-manifolds, in Proceedings of the Kirbyfest, Berkeley, CA, 1998, Geometry & Topology Monographs, vol. 2 (Mathematical Sciences Publishers, Coventry, 1999), 473–488; MR1734421 (2001b:57073).Google Scholar
Ruberman, D., Positive scalar curvature, diffeomorphisms and the Seiberg–Witten invariants, Geom. Topol. 5 (2001), 895–924; MR1874146 (2002k:57076).CrossRefGoogle Scholar
Ruberman, D. and Strle, S., Mod  $2$ Seiberg-Witten invariants of homology tori, Math. Res. Lett. 7 (2000), 789–799; MR1809302.CrossRefGoogle Scholar
$2$ Seiberg-Witten invariants of homology tori, Math. Res. Lett. 7 (2000), 789–799; MR1809302.CrossRefGoogle Scholar
Rudyak, Y., Piecewise linear structures on topological manifolds (World Scientific, Hackensack, NJ, 2016); MR3467983.CrossRefGoogle Scholar
Schultz, R., Smoothable submanifolds of a smooth manifold, available at http://math.ucr.edu/res/miscpapers/smoothablesubmflds.pdf.Google Scholar
Segal, G., Equivariant contractibility of the general linear group of Hilbert space, Bull. London Math. Soc. 1 (1969), 329–331; MR0248877.CrossRefGoogle Scholar
Szymik, M., Characteristic cohomotopy classes for families of 4-manifolds, Forum Math. 22 (2010), 509–523; MR2652709.CrossRefGoogle Scholar
Wall, C. T., Diffeomorphisms of  $4$-manifolds, J. London Math. Soc. s1-39 (1964), 131–140.CrossRefGoogle Scholar
$4$-manifolds, J. London Math. Soc. s1-39 (1964), 131–140.CrossRefGoogle Scholar
Watanabe, T., Some exotic nontrivial elements of the rational homotopy groups of Diff(S 4), Preprint (2018), arXiv:1812.02448.Google Scholar
- 8
- Cited by


