Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhargava, Manjul
Klagsbrun, Zev
Lemke Oliver, Robert J.
and
Shnidman, Ari
2019.
3-Isogeny Selmer groups and ranks of Abelian varieties in quadratic twist families over a number field.
Duke Mathematical Journal,
Vol. 168,
Issue. 15,
Bhargava, Manjul
Shankar, Arul
and
Wang, Xiaoheng
2022.
Squarefree values of polynomial discriminants I.
Inventiones mathematicae,
Vol. 228,
Issue. 3,
p.
1037.
Dao, Van Thinh
2022.
Average size of 2-Selmer groups of Jacobians of odd hyperelliptic curves over function fields.
Pacific Journal of Mathematics,
Vol. 319,
Issue. 2,
p.
259.
Bhargava, Manjul
Shankar, Arul
and
Wang, Xiaoheng
2022.
An improvement on Schmidt’s bound on the number of number fields of bounded discriminant and small degree.
Forum of Mathematics, Sigma,
Vol. 10,
Issue. ,
Swaminathan, Ashvin A.
2023.
A new parametrization for ideal classes in rings defined by binary forms, and applications.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Sanjaya, Gian Cordana
and
Wang, Xiaoheng
2023.
On the squarefree values of $$a^4+b^3$$.
Mathematische Annalen,
Vol. 386,
Issue. 3-4,
p.
1237.
Thinh, Dao
2023.
2-Selmer groups of even hyperelliptic curves over function fields.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 7,
p.
4679.
Beneish, Lea
and
Keyes, Christopher
2023.
On the proportion of locally soluble superelliptic curves.
Finite Fields and Their Applications,
Vol. 85,
Issue. ,
p.
102128.
Laga, Jef
2023.
Arithmetic statistics of Prym surfaces.
Mathematische Annalen,
Vol. 386,
Issue. 1-2,
p.
247.
Swaminathan, Ashvin A.
2024.
Most odd-degree binary forms fail to primitively represent a square.
Compositio Mathematica,
Vol. 160,
Issue. 3,
p.
481.
Laga, Jef
and
Swaminathan, Ashvin A
2024.
A Positive Proportion of Monic Odd-Degree Hyperelliptic Curves of Genus g ≥ 4 Have no Unexpected Quadratic Points.
International Mathematics Research Notices,
Vol. 2024,
Issue. 19,
p.
12857.
Frei, Sarah
and
Ji, Lena
2024.
A threefold violating a local-to-global principle for rationality.
Research in Number Theory,
Vol. 10,
Issue. 2,
Fisher, Tom
and
Liu, Mengzhen
2025.
Minimisation of 2-coverings of genus 2 Jacobians.
manuscripta mathematica,
Vol. 176,
Issue. 1,
Shankar, Arul
Siad, Artane
Swaminathan, Ashvin A.
and
Varma, Ila
2025.
Geometry-of-numbers methods in the cusp.
Algebra & Number Theory,
Vol. 19,
Issue. 6,
p.
1099.
Oller, Martí
2025.
The density of ADE families of curves having squarefree discriminant.
Journal de théorie des nombres de Bordeaux,
Vol. 37,
Issue. 3,
p.
989.
Romano, Beth
and
Thorne, Jack A.
2025.
An LLL algorithm with symmetries.
International Journal of Number Theory,
Vol. 21,
Issue. 06,
p.
1361.
Iyer, J.N.
Parimala, R.
and
Ramanan, S.
2025.
Period-index problem for hyperelliptic curves.
Advances in Mathematics,
Vol. 482,
Issue. ,
p.
110567.
Oller, Martí
2026.
Geometry-of-numbers over number fields and the density of ADE families of curves having squarefree discriminant.
Journal of Number Theory,
Vol. 281,
Issue. ,
p.
492.
Beneish, Lea
and
Keyes, Christopher
2026.
Fields generated by points on superelliptic curves.
Journal of Number Theory,
Vol. 278,
Issue. ,
p.
380.
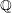 $\mathbb{Q}$ having a fixed genus
$\mathbb{Q}$ having a fixed genus  $n$ and a marked rational non-Weierstrass point. We show that when
$n$ and a marked rational non-Weierstrass point. We show that when 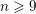 $n\geqslant 9$ , a positive proportion of these curves have exactly two rational points, and that this proportion tends to one as
$n\geqslant 9$ , a positive proportion of these curves have exactly two rational points, and that this proportion tends to one as  $n$ tends to infinity. We study rational points on these curves by first obtaining results on the 2-Selmer groups of their Jacobians. In this direction, we prove that the average size of the 2-Selmer groups of the Jacobians of curves in our family is bounded above by 6, which implies a bound of
$n$ tends to infinity. We study rational points on these curves by first obtaining results on the 2-Selmer groups of their Jacobians. In this direction, we prove that the average size of the 2-Selmer groups of the Jacobians of curves in our family is bounded above by 6, which implies a bound of 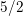 $5/2$ on the average rank of these Jacobians. Our results are natural extensions of Poonen and Stoll [Most odd degree hyperelliptic curves have only one rational point, Ann. of Math. (2) 180 (2014), 1137–1166] and Bhargava and Gross [The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point, in Automorphic representations and
$5/2$ on the average rank of these Jacobians. Our results are natural extensions of Poonen and Stoll [Most odd degree hyperelliptic curves have only one rational point, Ann. of Math. (2) 180 (2014), 1137–1166] and Bhargava and Gross [The average size of the 2-Selmer group of Jacobians of hyperelliptic curves having a rational Weierstrass point, in Automorphic representations and 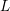 $L$ -functions, Tata Inst. Fundam. Res. Stud. Math., vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 23–91], where the analogous results are proved for the family of hyperelliptic curves with a marked rational Weierstrass point.
$L$ -functions, Tata Inst. Fundam. Res. Stud. Math., vol. 22 (Tata Institute of Fundamental Research, Mumbai, 2013), 23–91], where the analogous results are proved for the family of hyperelliptic curves with a marked rational Weierstrass point.
