Article contents
On the topology of Diophantine approximation spectra
Published online by Cambridge University Press: 02 May 2017
Abstract
Fix an integer 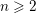 $n\geqslant 2$ . To each non-zero point
$n\geqslant 2$ . To each non-zero point 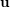 $\mathbf{u}$ in
$\mathbf{u}$ in 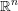 $\mathbb{R}^{n}$ , one attaches several numbers called exponents of Diophantine approximation. However, as Khintchine first observed, these numbers are not independent of each other. This raises the problem of describing the set of all possible values that a given family of exponents can take by varying the point
$\mathbb{R}^{n}$ , one attaches several numbers called exponents of Diophantine approximation. However, as Khintchine first observed, these numbers are not independent of each other. This raises the problem of describing the set of all possible values that a given family of exponents can take by varying the point 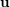 $\mathbf{u}$ . To avoid trivialities, one restricts to points
$\mathbf{u}$ . To avoid trivialities, one restricts to points 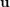 $\mathbf{u}$ whose coordinates are linearly independent over
$\mathbf{u}$ whose coordinates are linearly independent over 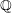 $\mathbb{Q}$ . The resulting set of values is called the spectrum of these exponents. We show that, in an appropriate setting, any such spectrum is a compact connected set. In the case
$\mathbb{Q}$ . The resulting set of values is called the spectrum of these exponents. We show that, in an appropriate setting, any such spectrum is a compact connected set. In the case 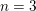 $n=3$ , we prove moreover that it is a semi-algebraic set closed under component-wise minimum. For
$n=3$ , we prove moreover that it is a semi-algebraic set closed under component-wise minimum. For 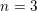 $n=3$ , we also obtain a description of the spectrum of the exponents
$n=3$ , we also obtain a description of the spectrum of the exponents 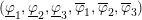 $(\text{}\underline{\unicode[STIX]{x1D711}}_{1},\text{}\underline{\unicode[STIX]{x1D711}}_{2},\text{}\underline{\unicode[STIX]{x1D711}}_{3},\overline{\unicode[STIX]{x1D711}}_{1},\overline{\unicode[STIX]{x1D711}}_{2},\overline{\unicode[STIX]{x1D711}}_{3})$ recently introduced by Schmidt and Summerer.
$(\text{}\underline{\unicode[STIX]{x1D711}}_{1},\text{}\underline{\unicode[STIX]{x1D711}}_{2},\text{}\underline{\unicode[STIX]{x1D711}}_{3},\overline{\unicode[STIX]{x1D711}}_{1},\overline{\unicode[STIX]{x1D711}}_{2},\overline{\unicode[STIX]{x1D711}}_{3})$ recently introduced by Schmidt and Summerer.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 5
- Cited by

