Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ichino, Atsushi
and
Ikeda, Tamutsu
2010.
On the Periods of Automorphic Forms on Special Orthogonal Groups and the Gross–Prasad Conjecture.
Geometric and Functional Analysis,
Vol. 19,
Issue. 5,
p.
1378.
Yamana, Shunsuke
2010.
On the lifting of elliptic cusp forms to cusp forms on quaternionic unitary groups.
Journal of Number Theory,
Vol. 130,
Issue. 11,
p.
2480.
Hentschel, Michael
Krieg, Aloys
and
Nebe, Gabriele
2010.
On the classification of lattices over $\mathbb{Q}(\sqrt{-3})$ , which are even unimodular ℤ-lattices.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 80,
Issue. 2,
p.
183.
Katsurada, Hidenori
and
Kawamura, Hisa-aki
2015.
Ikeda's conjecture on the period of the Duke–Imamoḡlu–Ikeda lift.
Proceedings of the London Mathematical Society,
Vol. 111,
Issue. 2,
p.
445.
Katsurada, Hidenori
2015.
Koecher–Maass series of the Ikeda lift for U ( m , m ).
Kyoto Journal of Mathematics,
Vol. 55,
Issue. 2,
KLOSIN, Krzysztof
2015.
The Maass space for $U(2,2)$ and the Bloch–Kato conjecture for the symmetric square motive of a modular form.
Journal of the Mathematical Society of Japan,
Vol. 67,
Issue. 2,
Atobe, Hiraku
2015.
Pullbacks of Hermitian Maass lifts.
Journal of Number Theory,
Vol. 153,
Issue. ,
p.
158.
Kim, Henry H.
and
Yamauchi, Takuya
2016.
Cusp forms on the exceptional group of type .
Compositio Mathematica,
Vol. 152,
Issue. 2,
p.
223.
Yamana, Shunsuke
2017.
Siegel series for skew Hermitian forms over quaternion algebras.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 87,
Issue. 1,
p.
43.
Katsurada, Hidenori
2017.
On the period of the Ikeda lift for U(m, m).
Mathematische Zeitschrift,
Vol. 286,
Issue. 1-2,
p.
141.
Atobe, Hiraku
and
Kojima, Hisashi
2018.
On the Miyawaki lifts of hermitian modular forms.
Journal of Number Theory,
Vol. 185,
Issue. ,
p.
281.
Katsurada, Hidenori
2018.
Period of the adelic Ikeda lift for U(m, m).
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 88,
Issue. 1,
p.
67.
Nagaoka, Shoyu
and
Takemori, Sho
2018.
On the mod p kernel of the theta operator and Eisenstein series.
Journal of Number Theory,
Vol. 188,
Issue. ,
p.
281.
BERGER, TOBIAS
and
KLOSIN, KRZYSZTOF
2019.
Ap-ADIC HERMITIAN MAASS LIFT.
Glasgow Mathematical Journal,
Vol. 61,
Issue. 1,
p.
85.
Vu, An Hoa
2019.
Hermitian Maass lift for general level.
Journal of Number Theory,
Vol. 198,
Issue. ,
p.
250.
Kim, Henry H.
and
Yamauchi, Takuya
2019.
Non-vanishing of Miyawaki type lifts.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 89,
Issue. 2,
p.
117.
Brown, Jim
and
Klosin, Krzysztof
2020.
Congruence primes for automorphic forms on unitary groups and applications to the arithmetic of Ikeda lifts.
Kyoto Journal of Mathematics,
Vol. 60,
Issue. 1,
Yamana, Shunsuke
2020.
On the lifting of Hilbert cusp forms to Hilbert-Hermitian cusp forms.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5395.
Li, Yingkun
Narita, Hiro-aki
and
Pitale, Ameya
2020.
An explicit construction of non-tempered cusp forms on $$O(1,8n+1)$$.
Annales mathématiques du Québec,
Vol. 44,
Issue. 2,
p.
349.
Dummigan, Neil
and
Fretwell, Dan
2021.
Automorphic forms for some even unimodular lattices.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 91,
Issue. 1,
p.
29.

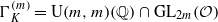 be the hermitian modular group of degree
be the hermitian modular group of degree 