Article contents
On the de Rham homology and cohomology of a complete local ring in equicharacteristic zero
Published online by Cambridge University Press: 07 August 2017
Abstract
Let 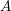 $A$ be a complete local ring with a coefficient field
$A$ be a complete local ring with a coefficient field 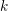 $k$ of characteristic zero, and let
$k$ of characteristic zero, and let 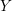 $Y$ be its spectrum. The de Rham homology and cohomology of
$Y$ be its spectrum. The de Rham homology and cohomology of 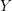 $Y$ have been defined by R. Hartshorne using a choice of surjection
$Y$ have been defined by R. Hartshorne using a choice of surjection 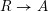 $R\rightarrow A$ where
$R\rightarrow A$ where 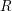 $R$ is a complete regular local
$R$ is a complete regular local 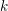 $k$ -algebra: the resulting objects are independent of the chosen surjection. We prove that the Hodge–de Rham spectral sequences abutting to the de Rham homology and cohomology of
$k$ -algebra: the resulting objects are independent of the chosen surjection. We prove that the Hodge–de Rham spectral sequences abutting to the de Rham homology and cohomology of 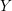 $Y$ , beginning with their
$Y$ , beginning with their 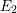 $E_{2}$ -terms, are independent of the chosen surjection (up to a degree shift in the homology case) and consist of finite-dimensional
$E_{2}$ -terms, are independent of the chosen surjection (up to a degree shift in the homology case) and consist of finite-dimensional 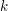 $k$ -spaces. These
$k$ -spaces. These 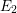 $E_{2}$ -terms therefore provide invariants of
$E_{2}$ -terms therefore provide invariants of  $A$ analogous to the Lyubeznik numbers. As part of our proofs we develop a theory of Matlis duality in relation to
$A$ analogous to the Lyubeznik numbers. As part of our proofs we develop a theory of Matlis duality in relation to 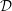 ${\mathcal{D}}$ -modules that is of independent interest. Some of the highlights of this theory are that if
${\mathcal{D}}$ -modules that is of independent interest. Some of the highlights of this theory are that if 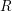 $R$ is a complete regular local ring containing
$R$ is a complete regular local ring containing 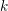 $k$ and
$k$ and 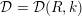 ${\mathcal{D}}={\mathcal{D}}(R,k)$ is the ring of
${\mathcal{D}}={\mathcal{D}}(R,k)$ is the ring of 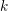 $k$ -linear differential operators on
$k$ -linear differential operators on 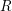 $R$ , then the Matlis dual
$R$ , then the Matlis dual 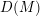 $D(M)$ of any left
$D(M)$ of any left 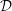 ${\mathcal{D}}$ -module
${\mathcal{D}}$ -module 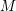 $M$ can again be given a structure of left
$M$ can again be given a structure of left 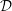 ${\mathcal{D}}$ -module, and if
${\mathcal{D}}$ -module, and if 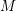 $M$ is a holonomic
$M$ is a holonomic 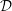 ${\mathcal{D}}$ -module, then the de Rham cohomology spaces of
${\mathcal{D}}$ -module, then the de Rham cohomology spaces of 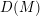 $D(M)$ are
$D(M)$ are 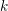 $k$ -dual to those of
$k$ -dual to those of 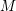 $M$ .
$M$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 12
- Cited by

