Article contents
On categories 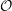 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
Published online by Cambridge University Press: 07 September 2017
Abstract
In this paper we study categories 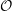 ${\mathcal{O}}$ over quantizations of symplectic resolutions admitting Hamiltonian tori actions with finitely many fixed points. In this generality, these categories were introduced by Braden et al. We establish a family of standardly stratified structures (in the sense of the author and Webster) on these categories
${\mathcal{O}}$ over quantizations of symplectic resolutions admitting Hamiltonian tori actions with finitely many fixed points. In this generality, these categories were introduced by Braden et al. We establish a family of standardly stratified structures (in the sense of the author and Webster) on these categories 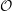 ${\mathcal{O}}$ . We use these structures to study shuffling functors of Braden et al. (called cross-walling functors in this paper). Most importantly, we prove that all cross-walling functors are derived equivalences that define an action of the Deligne groupoid of a suitable real hyperplane arrangement.
${\mathcal{O}}$ . We use these structures to study shuffling functors of Braden et al. (called cross-walling functors in this paper). Most importantly, we prove that all cross-walling functors are derived equivalences that define an action of the Deligne groupoid of a suitable real hyperplane arrangement.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
Baranovsky, V., Ginzburg, V., Kaledin, D. and Pecharich, J.,
Quantization of line bundles on Lagrangian subvarieties
, Selecta Math.
25 (2016), 1–25.CrossRefGoogle Scholar
Bezrukavnikov, R. and Kaledin, D.,
Fedosov quantization in the algebraic context
, Mosc. Math. J.
4 (2004), 559–592.CrossRefGoogle Scholar
Bezrukavnikov, R. and Losev, I., Etingof conjecture for quantized quiver varieties, Preprint (2013), arXiv:1309.1716.Google Scholar
Bialynicki-Birula, A.,
Some properties of the decompositions of algebraic varieties determined by actions of a torus
, Bull. Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys.
24 (1976), 667–674.Google Scholar
Braden, T., Licata, A., Proudfoot, N. and Webster, B.,
Quantizations of conical symplectic resolutions II: category O and symplectic duality
, Astérisque
384 (2016), 75–179.Google Scholar
Braden, T., Proudfoot, N. and Webster, B.,
Quantizations of conical symplectic resolutions I: local and global structure
, Astérisque
384 (2016), 1–73.Google Scholar
Cline, E., Parshall, B. and Scott, L.,
Stratifying endomorphism algebras
, Mem. Amer. Math. Soc.
124 (1996), no. 591.Google Scholar
Ginzburg, V., Guay, N., Opdam, E. and Rouquier, R.,
On the category 𝓞 for rational Cherednik algebras
, Invent. Math.
154 (2003), 617–651.Google Scholar
Gordon, I.,
Quiver varieties, category O for rational Cherednik algebras, and Hecke algebras
, Int. Math. Res. Pap. IMRP (2008), Art. ID rpn006.Google Scholar
Gordon, I. and Losev, I.,
On category 𝓞 for cyclotomic rational Cherednik algebras
, J. Eur. Math. Soc.
16 (2014), 1017–1079.CrossRefGoogle Scholar
Kaledin, D.,
On the coordinate ring of a projective Poisson scheme
, Math. Res. Lett.
13 (2006), 99–107.Google Scholar
Kaledin, D.,
Symplectic singularities from the Poisson point of view
, J. reine angew. Math.
600 (2006), 135–156.Google Scholar
Losev, I. V.,
Finite dimensional representations of W-algebras
, Duke Math. J.
159 (2011), 99–143.Google Scholar
Losev, I.,
Isomorphisms of quantizations via quantization of resolutions
, Adv. Math.
231 (2012), 1216–1270.CrossRefGoogle Scholar
Losev, I.,
Holonomic modules and Bernstein inequality
, Adv. Math.
308 (2017), 941–963.Google Scholar
Losev, I. and Webster, B.,
On uniqueness of tensor products of irreducible categorifications
, Selecta Math.
21 (2015), 345–377.CrossRefGoogle Scholar
Maulik, D. and Okounkov, A., Quantum groups and quantum cohomology, Preprint (2012), arXiv:1211.1287.Google Scholar
Namikawa, Y.,
Flops and Poisson deformations of symplectic varieties
, Publ. Res. Inst. Math. Sci.
44 (2008), 259–314.CrossRefGoogle Scholar
Namikawa, Y.,
Poisson deformations and birational geometry
, J. Math. Sci. Univ. Tokyo
22 (2015), 339–359.Google Scholar
- 6
- Cited by

