Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kishimoto, Takashi
2010.
Corrigendum: ‘A new proof of the non-tameness of the Nagata automorphism from the point of view of the Sarkisov Program, Compositio Math. 144 (2008), 963–977’.
Compositio Mathematica,
Vol. 146,
Issue. 4,
p.
999.
Hakuta, Keisuke
Sato, Hisayoshi
and
Takagi, Tsuyoshi
2016.
On tameness of Matsumoto-Imai central maps in three variables over the finite field $\mathbb F_2$.
Advances in Mathematics of Communications,
Vol. 10,
Issue. 2,
p.
221.

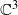 . For a long time, it remained unknown whether or not the Nagata automorphism is tame until Shestakov and Umirbaev at last proved that it is not tame in 2004, by purely algebraic methods (e.g. Poisson algebra). In this paper, we consider a certain necessary condition for a given automorphism on
. For a long time, it remained unknown whether or not the Nagata automorphism is tame until Shestakov and Umirbaev at last proved that it is not tame in 2004, by purely algebraic methods (e.g. Poisson algebra). In this paper, we consider a certain necessary condition for a given automorphism on 