Article contents
A new proof of Halász’s theorem, and its consequences
Published online by Cambridge University Press: 23 November 2018
Abstract
Halász’s theorem gives an upper bound for the mean value of a multiplicative function 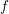 $f$. The bound is sharp for general such
$f$. The bound is sharp for general such 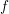 $f$, and, in particular, it implies that a multiplicative function with
$f$, and, in particular, it implies that a multiplicative function with 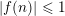 $|f(n)|\leqslant 1$ has either mean value
$|f(n)|\leqslant 1$ has either mean value 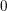 $0$, or is ‘close to’
$0$, or is ‘close to’ 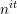 $n^{it}$ for some fixed
$n^{it}$ for some fixed 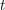 $t$. The proofs in the current literature have certain features that are difficult to motivate and which are not particularly flexible. In this article we supply a different, more flexible, proof, which indicates how one might obtain asymptotics, and can be modified to treat short intervals and arithmetic progressions. We use these results to obtain new, arguably simpler, proofs that there are always primes in short intervals (Hoheisel’s theorem), and that there are always primes near to the start of an arithmetic progression (Linnik’s theorem).
$t$. The proofs in the current literature have certain features that are difficult to motivate and which are not particularly flexible. In this article we supply a different, more flexible, proof, which indicates how one might obtain asymptotics, and can be modified to treat short intervals and arithmetic progressions. We use these results to obtain new, arguably simpler, proofs that there are always primes in short intervals (Hoheisel’s theorem), and that there are always primes near to the start of an arithmetic progression (Linnik’s theorem).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
Footnotes
A.G. has received funding in aid of this research from the European Research Council grant agreement no 670239, and from NSERC Canada under the CRC program. A.H. was supported, for parts of the research, by a postdoctoral fellowship from the Centre de recherches mathématiques in Montréal, and by a research fellowship at Jesus College, Cambridge. K.S. was partially supported by NSF grant DMS 1500237, and a Simons Investigator grant from the Simons Foundation. In addition, part of this work was carried out at MSRI, Berkeley during the Spring semester of 2017, supported in part by NSF grant DMS 1440140.
References
- 18
- Cited by

