Article contents
Matching of orbital integrals (transfer) and Roche Hecke algebra isomorphisms
Published online by Cambridge University Press: 21 January 2020
Abstract
Let 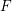 $F$ be a non-Archimedean local field,
$F$ be a non-Archimedean local field, 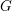 $G$ a connected reductive group defined and split over
$G$ a connected reductive group defined and split over 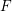 $F$, and
$F$, and 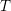 $T$ a maximal
$T$ a maximal 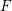 $F$-split torus in
$F$-split torus in 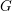 $G$. Let
$G$. Let 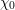 $\unicode[STIX]{x1D712}_{0}$ be a depth-zero character of the maximal compact subgroup
$\unicode[STIX]{x1D712}_{0}$ be a depth-zero character of the maximal compact subgroup 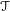 $T$ of
$T$ of 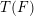 $T(F)$. This gives by inflation a character
$T(F)$. This gives by inflation a character 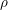 $\unicode[STIX]{x1D70C}$ of an Iwahori subgroup
$\unicode[STIX]{x1D70C}$ of an Iwahori subgroup 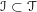 $\unicode[STIX]{x2110}\subset T$ of
$\unicode[STIX]{x2110}\subset T$ of 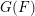 $G(F)$. From Roche [Types and Hecke algebras for principal series representations of split reductive
$G(F)$. From Roche [Types and Hecke algebras for principal series representations of split reductive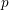 $p$-adic groups, Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 361–413],
$p$-adic groups, Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 361–413], 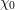 $\unicode[STIX]{x1D712}_{0}$ defines a reductive
$\unicode[STIX]{x1D712}_{0}$ defines a reductive 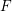 $F$-split group
$F$-split group 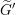 $\widetilde{G}^{\prime }$ whose connected component
$\widetilde{G}^{\prime }$ whose connected component 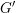 $G^{\prime }$ is an endoscopic group of
$G^{\prime }$ is an endoscopic group of 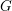 $G$, and there is an isomorphism of
$G$, and there is an isomorphism of 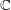 $\mathbb{C}$-algebras
$\mathbb{C}$-algebras 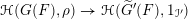 $\unicode[STIX]{x210B}(G(F),\unicode[STIX]{x1D70C})\rightarrow \unicode[STIX]{x210B}(\widetilde{G}^{\prime }(F),1_{\unicode[STIX]{x2110}^{\prime }})$ where
$\unicode[STIX]{x210B}(G(F),\unicode[STIX]{x1D70C})\rightarrow \unicode[STIX]{x210B}(\widetilde{G}^{\prime }(F),1_{\unicode[STIX]{x2110}^{\prime }})$ where 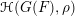 $\unicode[STIX]{x210B}(G(F),\unicode[STIX]{x1D70C})$ is the Hecke algebra of compactly supported
$\unicode[STIX]{x210B}(G(F),\unicode[STIX]{x1D70C})$ is the Hecke algebra of compactly supported 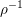 $\unicode[STIX]{x1D70C}^{-1}$-spherical functions on
$\unicode[STIX]{x1D70C}^{-1}$-spherical functions on 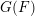 $G(F)$ and
$G(F)$ and 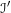 $\unicode[STIX]{x2110}^{\prime }$ is an Iwahori subgroup of
$\unicode[STIX]{x2110}^{\prime }$ is an Iwahori subgroup of 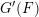 $G^{\prime }(F)$. This isomorphism gives by restriction an injective morphism
$G^{\prime }(F)$. This isomorphism gives by restriction an injective morphism 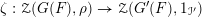 $\unicode[STIX]{x1D701}:Z(G(F),\unicode[STIX]{x1D70C})\rightarrow Z(G^{\prime }(F),1_{\unicode[STIX]{x2110}^{\prime }})$ between the centers of the Hecke algebras. We prove here that a certain linear combination of morphisms analogous to
$\unicode[STIX]{x1D701}:Z(G(F),\unicode[STIX]{x1D70C})\rightarrow Z(G^{\prime }(F),1_{\unicode[STIX]{x2110}^{\prime }})$ between the centers of the Hecke algebras. We prove here that a certain linear combination of morphisms analogous to 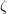 $\unicode[STIX]{x1D701}$ realizes the transfer (matching of strongly
$\unicode[STIX]{x1D701}$ realizes the transfer (matching of strongly 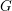 $G$-regular semi-simple orbital integrals). If
$G$-regular semi-simple orbital integrals). If 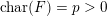 $\operatorname{char}(F)=p>0$, our result is unconditional only if
$\operatorname{char}(F)=p>0$, our result is unconditional only if 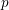 $p$ is large enough.
$p$ is large enough.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
Footnotes
The authors acknowledge partial support by the Agence Nationale de la Recherche, project ANR–13–BS01–00120–02 FERPLAY.
References
- 1
- Cited by

