Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dimca, Alexandru
and
Sticlaru, Gabriel
2019.
Saturation of Jacobian ideals: Some applications to nearly free curves, line arrangements and rational cuspidal plane curves.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 12,
p.
5055.
Dimca, Alexandru
and
Sticlaru, Gabriel
2019.
On supersolvable and nearly supersolvable line arrangements.
Journal of Algebraic Combinatorics,
Vol. 50,
Issue. 4,
p.
363.
Abe, Takuro
and
Dimca, Alexandru
2020.
On complex supersolvable line arrangements.
Journal of Algebra,
Vol. 552,
Issue. ,
p.
38.
Dumnicki, Marcin
Farnik, Łucja
Harbourne, Brian
Malara, Grzegorz
Szpond, Justyna
and
Tutaj-Gasińska, Halszka
2020.
A matrixwise approach to unexpected hypersurfaces.
Linear Algebra and its Applications,
Vol. 592,
Issue. ,
p.
113.
Szpond, Justyna
2020.
Combinatorial Structures in Algebra and Geometry.
Vol. 331,
Issue. ,
p.
161.
Szpond, Justyna
2020.
Unexpected curves and Togliatti‐type surfaces.
Mathematische Nachrichten,
Vol. 293,
Issue. 1,
p.
158.
Di Marca, Michela
Malara, Grzegorz
and
Oneto, Alessandro
2020.
Unexpected curves arising from special line arrangements.
Journal of Algebraic Combinatorics,
Vol. 51,
Issue. 2,
p.
171.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
111.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
137.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
103.
Kabat, Jakub
and
Strycharz-Szemberg, Beata
2020.
Diminished Fermat-type arrangements and unexpected curves.
Comptes Rendus. Mathématique,
Vol. 358,
Issue. 5,
p.
603.
Juhnke‐Kubitzke, Martina
and
Nagel, Uwe
2020.
Squeezed complexes.
Journal of the London Mathematical Society,
Vol. 101,
Issue. 1,
p.
110.
Bauer, Thomas
Malara, Grzegorz
Szemberg, Tomasz
and
Szpond, Justyna
2020.
Quartic unexpected curves and surfaces.
manuscripta mathematica,
Vol. 161,
Issue. 3-4,
p.
283.
Harbourne, B.
2021.
Commutative Algebra.
p.
445.
Abe, Takuro
Dimca, Alexandru
and
Sticlaru, Gabriel
2021.
Addition–deletion results for the minimal degree of logarithmic derivations of hyperplane arrangements and maximal Tjurina line arrangements.
Journal of Algebraic Combinatorics,
Vol. 54,
Issue. 3,
p.
739.
Harbourne, Brian
Migliore, Juan
and
Tutaj-Gasińska, Halszka
2021.
New constructions of unexpected hypersurfaces in $$\mathbb {P}^n$$.
Revista Matemática Complutense,
Vol. 34,
Issue. 1,
p.
1.
Chmiel, Natalia
2021.
Actual and virtual dimension of codimension 2 general linear subspaces in $${\mathbb {P}}^n$$.
Geometriae Dedicata,
Vol. 215,
Issue. 1,
p.
51.
Hanumanthu, Krishna
and
Harbourne, Brian
2021.
Real and complex supersolvable line arrangements in the projective plane.
Journal of Algebraic Combinatorics,
Vol. 54,
Issue. 3,
p.
767.
Malara, Grzegorz
Pokora, Piotr
and
Tutaj-Gasińska, Halszka
2021.
On 3-syzygy and unexpected plane curves.
Geometriae Dedicata,
Vol. 214,
Issue. 1,
p.
49.
Migliore, Juan
and
Nagel, Uwe
2021.
The Lefschetz question for ideals generated by powers of linear forms in few variables.
Journal of Commutative Algebra,
Vol. 13,
Issue. 3,
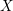 $X$ of fat points imposes on the complete linear system of curves in
$X$ of fat points imposes on the complete linear system of curves in 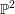 $\mathbb{P}^{2}$ of fixed degree
$\mathbb{P}^{2}$ of fixed degree  $d$, in terms of the occurrence of certain rational curves in the base locus of the linear subsystem defined by
$d$, in terms of the occurrence of certain rational curves in the base locus of the linear subsystem defined by 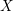 $X$. As a first step towards a new theory, we show that rational curves play a similar role in a special case of a generalized problem, which asks how many conditions are imposed by a general union of fat points on linear subsystems defined by imposed base points. Moreover, motivated by work of Di Gennaro, Ilardi and Vallès and of Faenzi and Vallès, we relate our results to the failure of a strong Lefschetz property, and we give a Lefschetz-like criterion for Terao’s conjecture on the freeness of line arrangements.
$X$. As a first step towards a new theory, we show that rational curves play a similar role in a special case of a generalized problem, which asks how many conditions are imposed by a general union of fat points on linear subsystems defined by imposed base points. Moreover, motivated by work of Di Gennaro, Ilardi and Vallès and of Faenzi and Vallès, we relate our results to the failure of a strong Lefschetz property, and we give a Lefschetz-like criterion for Terao’s conjecture on the freeness of line arrangements.
