Article contents
The homotopy theory of polyhedral products associated with flag complexes
Published online by Cambridge University Press: 23 November 2018
Abstract
If 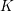 $K$ is a simplicial complex on
$K$ is a simplicial complex on 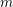 $m$ vertices, the flagification of
$m$ vertices, the flagification of 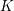 $K$ is the minimal flag complex
$K$ is the minimal flag complex 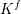 $K^{f}$ on the same vertex set that contains
$K^{f}$ on the same vertex set that contains 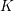 $K$. Letting
$K$. Letting 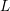 $L$ be the set of vertices, there is a sequence of simplicial inclusions
$L$ be the set of vertices, there is a sequence of simplicial inclusions 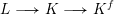 $L\stackrel{}{\longrightarrow }K\stackrel{}{\longrightarrow }K^{f}$. This induces a sequence of maps of polyhedral products
$L\stackrel{}{\longrightarrow }K\stackrel{}{\longrightarrow }K^{f}$. This induces a sequence of maps of polyhedral products 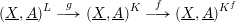 $(\text{}\underline{X},\text{}\underline{A})^{L}\stackrel{g}{\longrightarrow }(\text{}\underline{X},\text{}\underline{A})^{K}\stackrel{f}{\longrightarrow }(\text{}\underline{X},\text{}\underline{A})^{K^{f}}$. We show that
$(\text{}\underline{X},\text{}\underline{A})^{L}\stackrel{g}{\longrightarrow }(\text{}\underline{X},\text{}\underline{A})^{K}\stackrel{f}{\longrightarrow }(\text{}\underline{X},\text{}\underline{A})^{K^{f}}$. We show that 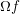 $\unicode[STIX]{x1D6FA}f$ and
$\unicode[STIX]{x1D6FA}f$ and 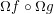 $\unicode[STIX]{x1D6FA}f\circ \unicode[STIX]{x1D6FA}g$ have right homotopy inverses and draw consequences. For a flag complex
$\unicode[STIX]{x1D6FA}f\circ \unicode[STIX]{x1D6FA}g$ have right homotopy inverses and draw consequences. For a flag complex 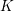 $K$ the polyhedral product of the form
$K$ the polyhedral product of the form 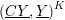 $(\text{}\underline{CY},\text{}\underline{Y})^{K}$ is a co-
$(\text{}\underline{CY},\text{}\underline{Y})^{K}$ is a co-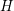 $H$-space if and only if the 1-skeleton of
$H$-space if and only if the 1-skeleton of 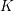 $K$ is a chordal graph, and we deduce that the maps
$K$ is a chordal graph, and we deduce that the maps 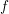 $f$ and
$f$ and 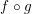 $f\circ g$ have right homotopy inverses in this case.
$f\circ g$ have right homotopy inverses in this case.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 12
- Cited by

