Hostname: page-component-784d4fb959-wvrvt Total loading time: 0 Render date: 2025-07-17T01:17:40.648Z Has data issue: false hasContentIssue false
  • English
  • Français

Hochschild homology of Hopf algebras and free Yetter–Drinfeld resolutions of the counit

Part of: Homological methods Selfadjoint operator algebras Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  17 December 2012

Julien Bichon
Julien Bichon*
Affiliation:
Laboratoire de Mathématiques, Université Blaise Pascal, Complexe universitaire des Cézeaux, 63171 Aubière cedex, France (email: julien.bichon@math.univ-bpclermont.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if 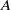$A$ and 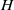$H$ are Hopf algebras that have equivalent tensor categories of comodules, then one can transport what we call a free Yetter–Drinfeld resolution of the counit of 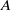$A$ to the same kind of resolution for the counit of 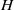$H$, exhibiting in this way strong links between the Hochschild homologies of 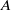$A$ and 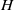$H$. This enables us to obtain a finite free resolution of the counit of 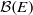$\mathcal {B}(E)$, the Hopf algebra of the bilinear form associated with an invertible matrix 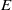$E$, generalizing an earlier construction of Collins, Härtel and Thom in the orthogonal case 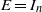$E=I_n$. It follows that 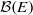$\mathcal {B}(E)$ is smooth of dimension 3 and satisfies Poincaré duality. Combining this with results of Vergnioux, it also follows that when 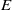$E$ is an antisymmetric matrix, the 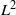$L^2$-Betti numbers of the associated discrete quantum group all vanish. We also use our resolution to compute the bialgebra cohomology of 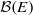$\mathcal {B}(E)$in the cosemisimple case.

Keywords

Hopf algebraHochschild homologyYetter–Drinfeld module$\uppercase {l}^2$-Betti numbers

MSC classification

Secondary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory 16T05: Hopf algebras and their applications

Information

Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 658 - 678
Copyright
Copyright © 2012 The Author(s)

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[Ban96]Banica, T., Théorie des représentations du groupe quantique compact libre $O(n)$, C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), 241–244.Google Scholar
[BC07]Banica, T. and Collins, B., Integration over compact quantum groups, Publ. Res. Inst. Math. Sci. 43 (2007), 277–302.Google Scholar
[BCZ09]Banica, T., Collins, B. and Zinn-Justin, P., Spectral analysis of the free orthogonal matrix, Int. Math. Res. Not. IMRN (2009), 3286–3309.Google Scholar
[Bic10]Bichon, J., Hopf–Galois objects and cogroupoids, Pub. Mat. Uruguay, to appear, arXiv:1006.3014.Google Scholar
[Bic03a]Bichon, J., The representation category of the quantum group of a non-degenerate bilinear form, Comm. Algebra 31 (2003), 4831–4851.CrossRefGoogle Scholar
[Bic03b]Bichon, J., Hopf–Galois systems, J. Algebra 264 (2003), 565–581.Google Scholar
[BDV06]Bichon, J., De Rijdt, A. and Vaes, S., Ergodic coactions with large multiplicity and monoidal equivalence of quantum groups, Comm. Math. Phys. 262 (2006), 703–728.Google Scholar
[BG02]Brown, K. A. and Goodearl, K. R, Lectures on algebraic quantum groups, Advanced Courses in Mathematics CRM Barcelona (Birkhäuser, Basel, 2002).Google Scholar
[BZ08]Brown, K. A. and Zhang, J. J., Dualising complexes and twisted Hochschild (co)homology for Noetherian Hopf algebras, J. Algebra 320 (2008), 1814–1850.Google Scholar
[CMZ97]Caenepeel, S., Militaru, G. and Zhu, S., Crossed modules and Doi–Hopf modules, Israel J. Math. 100 (1997), 221–247.Google Scholar
[CMZ02]Caenepeel, S., Militaru, G. and Zhu, S., Frobenius and separable functors for generalized module categories and nonlinear equations, Lecture Notes in Mathematics, vol. 1787 (Springer, Berlin, 2002).Google Scholar
[CE56]Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
[CHT09]Collins, B., Härtel, J. and Thom, A., Homology of free quantum groups, C. R. Math. Acad. Sci. Paris 347 (2009), 271–276.Google Scholar
[CS05]Connes, A. and Shlyakhtenko, D., $L^2$-homology for von Neumann algebras, J. Reine Angew. Math. 586 (2005), 125–168.Google Scholar
[DL90]Dubois-Violette, M. and Launer, G., The quantum group of a non-degenerate bilinear form, Phys. Lett. B 245 (1990), 175–177.CrossRefGoogle Scholar
[FT91]Feng, P. and Tsygan, B., Hochschild and cyclic homology of quantum groups, Comm. Math. Phys. 140 (1991), 481–521.CrossRefGoogle Scholar
[GS90]Gerstenhaber, M. and Schack, S., Bialgebra cohomology, deformations and quantum groups, Proc. Natl Acad. Sci. USA 87 (1990), 78–81.Google Scholar
[GS92]Gerstenhaber, M. and Schack, S., Algebras, bialgebras, quantum groups, and algebraic deformations, Contemp. Math. 134 (1992), 51–92.Google Scholar
[GK93]Ginzburg, V. and Kumar, S., Cohomology of quantum groups at roots of unity, Duke Math. J. 69 (1993), 179–198.Google Scholar
[Gru04]Grunspan, C., Hopf-Galois systems and Kashiwara algebras, Comm. Algebra 32 (2004), 3373–3389.Google Scholar
[HK05]Hadfield, T. and Krähmer, U., Twisted homology of quantum $\mathrm {SL}(2)$, K-Theory 34 (2005), 327–360.Google Scholar
[Kas95]Kassel, C., Quantum groups, Graduate Texts in Mathematics, vol. 155 (Springer, Berlin, 1995).CrossRefGoogle Scholar
[KS97]Klimyk, A. and Schmüdgen, K., Quantum groups and their representations, Texts and Monographs in Physics (Springer, Berlin, 1997).Google Scholar
[KK10]Kowalzig, N. and Krähmer, U., Duality and products in algebraic (co)homology theories, J. Algebra 323 (2010), 2063–2081.CrossRefGoogle Scholar
[Kye08]Kyed, D., $L^2$-homology for compact quantum groups, Math. Scand. 103 (2008), 111–129.Google Scholar
[Kye 11]Kyed, D., On the zeroth $L^2$-homology of a quantum group, Münster J. Math. 4 (2011), 119–128.Google Scholar
[Lin77]Lin, B. I., Semiperfect coalgebras, J. Algebra 49 (1977), 357–373.Google Scholar
[Luc98]Lück, W., Dimension theory of arbitrary modules over finite von Neumann algebras and $L^2$-Betti numbers. I. Foundations, J. Reine Angew. Math. 495 (1998), 135–162.Google Scholar
[Luc02]Lück, W., L 2-invariants: theory and applications to geometry and K-theory (Springer, Berlin, 2002).CrossRefGoogle Scholar
[Mon93]Montgomery, S., Hopf algebras and their actions on rings (American Mathematical Society, Providence, RI, 1993).Google Scholar
[PW90]Parshall, B. and Wang, J., On bialgebra cohomology, Bull. Soc. Math. Belg. Sér. A 42 (1990), 607–642.Google Scholar
[Sch94]Schauenburg, P., Hopf modules and Yetter–Drinfeld modules, J. Algebra 169 (1994), 874–890.Google Scholar
[Sch96]Schauenburg, P., Hopf bigalois extensions, Comm. Algebra 24 (1996), 3797–3825.Google Scholar
[Sch04]Schauenburg, P., Hopf-Galois and bi-Galois extensions, Fields Inst. Commun. 43 (2004), 469–515.Google Scholar
[Tai04a]Taillefer, R., Injective Hopf bimodules, cohomologies of infinite-dimensional Hopf algebras and graded-commutativity of the Yoneda product, J. Algebra 276 (2004), 259–279.Google Scholar
[Tai04b]Taillefer, R., Cohomology theories of Hopf bimodules and cup-product, Algebr. Represent. Theory 7 (2004), 471–490.Google Scholar
[Tai07]Taillefer, R., Bialgebra cohomology of the duals of a class of generalized Taft algebras, Comm. Algebra (2007), 1415–1420.Google Scholar
[Tho08]Thom, A., $L^2$-cohomology for von Neumann algebras, Geom. Funct. Anal. 18 (2008), 251–270.Google Scholar
[VV08]Vaes, S. and Vander Vennet, N., Identification of the Poisson and Martin boundaries of orthogonal discrete quantum groups, J. Inst. Math. Jussieu 7 (2008), 391–412.Google Scholar
[VV07]Vaes, S. and Vergnioux, R., The boundary of universal discrete quantum groups, exactness, and factoriality, Duke Math. J. 140 (2007), 35–84.Google Scholar
[VdB98]Van den Bergh, M., A relation between Hochschild homology and cohomology for Gorenstein rings, Proc. Amer. Math. Soc. 126 (1998), 1345–1348; Erratum: Proc. Amer. Math. Soc. 130 (2002), 2809–2810.Google Scholar
[Ver07]Vergnioux, R., The property of rapid decay for discrete quantum groups, J. Operator Theory 57 (2007), 303–324.Google Scholar
[Ver12]Vergnioux, R., Paths in quantum Cayley trees and $L^2$-cohomology, Adv. Math. 229 (2012), 2686–2711.Google Scholar
[Voi11]Voigt, C., The Baum–Connes conjecture for free orthogonal quantum groups, Adv. Math. 227 (2011), 1873–1913.Google Scholar
[Wan95]Wang, S., Free products of compact quantum groups, Comm. Math. Phys. 167 (1995), 671–692.CrossRefGoogle Scholar
[Wei94]Weibel, C., An Introduction to Homological Algebra (Cambridge University Press, Cambridge, 1994).Google Scholar
[Wor98]Woronowicz, S. L., Compact quantum groups, in Symétries quantiques (Les Houches, 1995) (North-Holland, Amsterdam, 1998), 845–884.Google Scholar