Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sheth, Mihir
2022.
On irreducible supersingular representations of
GL2(F).
Pacific Journal of Mathematics,
Vol. 321,
Issue. 2,
p.
431.
Breuil, Christophe
Herzig, Florian
Hu, Yongquan
Morra, Stefano
and
Schraen, Benjamin
2023.
Gelfand–Kirillov dimension and mod $p$ cohomology for $\operatorname{GL}_{2}$.
Inventiones mathematicae,
Vol. 234,
Issue. 1,
p.
1.
Le, Daniel
Hung, Bao V. Le
Levin, Brandon
and
Morra, Stefano
2023.
Local models for Galois deformation rings and applications.
Inventiones mathematicae,
Vol. 231,
Issue. 3,
p.
1277.
Schein, Michael M.
2023.
A family of irreducible supersingular representations of GL2(F) for some ramified p-adic fields.
Israel Journal of Mathematics,
Vol. 255,
Issue. 2,
p.
911.
Dospinescu, Gabriel
Paškūnas, Vytautas
and
Schraen, Benjamin
2023.
Gelfand–Kirillov dimension and the p-adic Jacquet–Langlands correspondence.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Le, Daniel
Le Hung, Bao V.
Levin, Brandon
and
Morra, Stefano
2024.
Serre weights for three-dimensional wildly ramified Galois representations.
Algebra & Number Theory,
Vol. 18,
Issue. 7,
p.
1221.
Le, Daniel
Le Hung, Bao
Morra, Stefano
Park, Chol
and
Qian, Zicheng
2024.
Colength one deformation rings.
Transactions of the American Mathematical Society,
Hu, Yongquan
and
Wang, Haoran
2024.
On some mod p representations of quaternion algebra over ℚp.
Compositio Mathematica,
Vol. 160,
Issue. 11,
p.
2585.
Breuil, Christophe
Herzig, Florian
Hu, Yongquan
Morra, Stefano
and
Schraen, Benjamin
2025.
Multivariable $$(\varphi ,\mathcal {O}_K^\times )$$-modules and local–global compatibility.
Mathematische Annalen,
Vol. 392,
Issue. 2,
p.
2709.
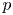 $p$ Langlands program for
$p$ Langlands program for 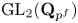 $\mathrm {GL}_2(\mathbf {Q}_{p^f})$. Namely, given a global residual representation
$\mathrm {GL}_2(\mathbf {Q}_{p^f})$. Namely, given a global residual representation 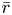 $\bar {r}$ appearing in the mod
$\bar {r}$ appearing in the mod 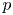 $p$ cohomology of a Shimura curve that is sufficiently generic at
$p$ cohomology of a Shimura curve that is sufficiently generic at  $p$ and satisfies a Taylor–Wiles hypothesis, we prove that the diagram occurring in the corresponding Hecke eigenspace of mod
$p$ and satisfies a Taylor–Wiles hypothesis, we prove that the diagram occurring in the corresponding Hecke eigenspace of mod 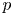 $p$ completed cohomology is determined by the restrictions of
$p$ completed cohomology is determined by the restrictions of 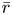 $\bar {r}$ to decomposition groups at
$\bar {r}$ to decomposition groups at  $p$. If these restrictions are moreover semisimple, we show that the
$p$. If these restrictions are moreover semisimple, we show that the 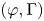 $(\varphi ,\Gamma )$-modules attached to this diagram by Breuil give, under Fontaine's equivalence, the tensor inductions of the duals of the restrictions of
$(\varphi ,\Gamma )$-modules attached to this diagram by Breuil give, under Fontaine's equivalence, the tensor inductions of the duals of the restrictions of 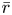 $\bar {r}$ to decomposition groups at
$\bar {r}$ to decomposition groups at 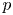 $p$.
$p$.