No CrossRef data available.
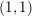 $(1,1)$ theorem
$(1,1)$ theoremPublished online by Cambridge University Press: 02 May 2019
In this paper we prove a semistable version of the variational Tate conjecture for divisors in crystalline cohomology, showing that for 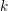 $k$ a perfect field of characteristic
$k$ a perfect field of characteristic 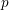 $p$, a rational (logarithmic) line bundle on the special fibre of a semistable scheme over
$p$, a rational (logarithmic) line bundle on the special fibre of a semistable scheme over  $k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ lifts to the total space if and only if its first Chern class does. The proof is elementary, using standard properties of the logarithmic de Rham–Witt complex. As a corollary, we deduce similar algebraicity lifting results for cohomology classes on varieties over global function fields. Finally, we give a counter-example to show that the variational Tate conjecture for divisors cannot hold with
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$ lifts to the total space if and only if its first Chern class does. The proof is elementary, using standard properties of the logarithmic de Rham–Witt complex. As a corollary, we deduce similar algebraicity lifting results for cohomology classes on varieties over global function fields. Finally, we give a counter-example to show that the variational Tate conjecture for divisors cannot hold with 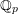 $\mathbb{Q}_{p}$-coefficients.
$\mathbb{Q}_{p}$-coefficients.