Article contents
Corrigendum: ‘On certain algebraic curves related to polynomial maps, Compositio Math. 103 (1996), 319–350’
Published online by Cambridge University Press: 18 June 2010
Abstract
An argument is given to fill a gap in a proof in the author’s article On certain algebraic curves related to polynomial maps, Compositio Math. 103 (1996), 319–350, that the polynomial Φn(x,c), whose roots are the periodic points of period n of a certain polynomial map x→f(x,c), is absolutely irreducible over the finite field of p elements, provided that f(x,1) has distinct roots and that the multipliers of the orbits of period n are also distinct over 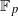 . Assuming that Φn(x,c) is reducible in characteristic p, we show that Hensel’s lemma and Laurent series expansions of the roots can be used to obtain a factorization of Φn(x,c) in characteristic 0, contradicting the absolute irreducibility of this polynomial over the rational field.
. Assuming that Φn(x,c) is reducible in characteristic p, we show that Hensel’s lemma and Laurent series expansions of the roots can be used to obtain a factorization of Φn(x,c) in characteristic 0, contradicting the absolute irreducibility of this polynomial over the rational field.
MSC classification
Information
- Type
- Corrigenda
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2010
References
- 3
- Cited by

