Article contents
Compatible systems and ramification
Published online by Cambridge University Press: 21 October 2019
Abstract
We show that compatible systems of 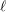 $\ell$-adic sheaves on a scheme of finite type over the ring of integers of a local field are compatible along the boundary up to stratification. This extends a theorem of Deligne on curves over a finite field. As an application, we deduce the equicharacteristic case of classical conjectures on
$\ell$-adic sheaves on a scheme of finite type over the ring of integers of a local field are compatible along the boundary up to stratification. This extends a theorem of Deligne on curves over a finite field. As an application, we deduce the equicharacteristic case of classical conjectures on 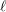 $\ell$-independence for proper smooth varieties over complete discrete valuation fields. Moreover, we show that compatible systems have compatible ramification. We also prove an analogue for integrality along the boundary.
$\ell$-independence for proper smooth varieties over complete discrete valuation fields. Moreover, we show that compatible systems have compatible ramification. We also prove an analogue for integrality along the boundary.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
The first author was partially supported by National Natural Science Foundation of China Grants 11371043 and 11501541. The second author was partially supported by National Natural Science Foundation of China Grants 11621061, 11688101 and 11822110 and the National Center for Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences.
References
- 3
- Cited by

