Article contents
Adelic descent theory
Published online by Cambridge University Press: 31 May 2017
Abstract
A result of André Weil allows one to describe rank  $n$ vector bundles on a smooth complete algebraic curve up to isomorphism via a double quotient of the set
$n$ vector bundles on a smooth complete algebraic curve up to isomorphism via a double quotient of the set 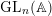 $\text{GL}_{n}(\mathbb{A})$ of regular matrices over the ring of adèles (over algebraically closed fields, this result is also known to extend to
$\text{GL}_{n}(\mathbb{A})$ of regular matrices over the ring of adèles (over algebraically closed fields, this result is also known to extend to  $G$ -torsors for a reductive algebraic group
$G$ -torsors for a reductive algebraic group 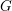 $G$ ). In the present paper we develop analogous adelic descriptions for vector and principal bundles on arbitrary Noetherian schemes, by proving an adelic descent theorem for perfect complexes. We show that for Beilinson’s co-simplicial ring of adèles
$G$ ). In the present paper we develop analogous adelic descriptions for vector and principal bundles on arbitrary Noetherian schemes, by proving an adelic descent theorem for perfect complexes. We show that for Beilinson’s co-simplicial ring of adèles 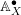 $\mathbb{A}_{X}^{\bullet }$ , we have an equivalence
$\mathbb{A}_{X}^{\bullet }$ , we have an equivalence 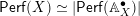 $\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$ between perfect complexes on
$\mathsf{Perf}(X)\simeq |\mathsf{Perf}(\mathbb{A}_{X}^{\bullet })|$ between perfect complexes on  $X$ and cartesian perfect complexes for
$X$ and cartesian perfect complexes for 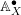 $\mathbb{A}_{X}^{\bullet }$ . Using the Tannakian formalism for symmetric monoidal
$\mathbb{A}_{X}^{\bullet }$ . Using the Tannakian formalism for symmetric monoidal 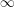 $\infty$ -categories, we conclude that a Noetherian scheme can be reconstructed from the co-simplicial ring of adèles. We view this statement as a scheme-theoretic analogue of Gelfand–Naimark’s reconstruction theorem for locally compact topological spaces from their ring of continuous functions. Several results for categories of perfect complexes over (a strong form of) flasque sheaves of algebras are established, which might be of independent interest.
$\infty$ -categories, we conclude that a Noetherian scheme can be reconstructed from the co-simplicial ring of adèles. We view this statement as a scheme-theoretic analogue of Gelfand–Naimark’s reconstruction theorem for locally compact topological spaces from their ring of continuous functions. Several results for categories of perfect complexes over (a strong form of) flasque sheaves of algebras are established, which might be of independent interest.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2017
References
- 2
- Cited by

