Article contents
Right-angled Artin groups as normal subgroups of mapping class groups
Published online by Cambridge University Press: 27 July 2021
Abstract
We construct the first examples of normal subgroups of mapping class groups that are isomorphic to non-free right-angled Artin groups. Our construction also gives normal, non-free right-angled Artin subgroups of other groups, such as braid groups and pure braid groups, as well as many subgroups of the mapping class group, such as the Torelli subgroup. Our work recovers and generalizes the seminal result of Dahmani–Guirardel–Osin, which gives free, purely pseudo-Anosov normal subgroups of mapping class groups. We give two applications of our methods: (1) we produce an explicit proper normal subgroup of the mapping class group that is not contained in any level 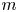 $m$ congruence subgroup and (2) we produce an explicit example of a pseudo-Anosov mapping class with the property that all of its even powers have free normal closure and its odd powers normally generate the entire mapping class group. The technical theorem at the heart of our work is a new version of the windmill apparatus of Dahmani–Guirardel–Osin, which is tailored to the setting of group actions on the projection complexes of Bestvina–Bromberg–Fujiwara.
$m$ congruence subgroup and (2) we produce an explicit example of a pseudo-Anosov mapping class with the property that all of its even powers have free normal closure and its odd powers normally generate the entire mapping class group. The technical theorem at the heart of our work is a new version of the windmill apparatus of Dahmani–Guirardel–Osin, which is tailored to the setting of group actions on the projection complexes of Bestvina–Bromberg–Fujiwara.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 3
- Cited by


