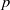 $p$-algebras
$p$-algebrasPublished online by Cambridge University Press: 22 May 2013
The main result of this paper states that if 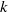 $k$ is a field of characteristic
$k$ is a field of characteristic 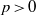 $p\gt 0$ and
$p\gt 0$ and 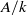 $A/ k$ is a central simple algebra of index
$A/ k$ is a central simple algebra of index 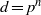 $d= {p}^{n} $ and exponent
$d= {p}^{n} $ and exponent 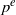 ${p}^{e} $, then
${p}^{e} $, then 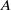 $A$ is split by a purely inseparable extension of
$A$ is split by a purely inseparable extension of 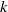 $k$ of the form
$k$ of the form 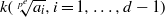 $k( \sqrt[{p}^{e} ]{{a}_{i} }, i= 1, \ldots , d- 1)$. Combining this result with a theorem of Albert (for which we include a new proof), we get that any such algebra is Brauer equivalent to the tensor product of at most
$k( \sqrt[{p}^{e} ]{{a}_{i} }, i= 1, \ldots , d- 1)$. Combining this result with a theorem of Albert (for which we include a new proof), we get that any such algebra is Brauer equivalent to the tensor product of at most 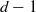 $d- 1$ cyclic algebras of degree
$d- 1$ cyclic algebras of degree 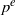 ${p}^{e} $. This gives a drastic improvement upon previously known upper bounds.
${p}^{e} $. This gives a drastic improvement upon previously known upper bounds.