Hostname: page-component-76c49bb84f-229nc Total loading time: 0 Render date: 2025-07-09T08:39:27.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Kloosterman paths and the shape of exponential sums

Part of: Finite fields and commutative rings (number-theoretic aspects) Exponential sums and character sums (Co)homology theory Stochastic processes Limit theorems

Published online by Cambridge University Press:  15 April 2016

Emmanuel Kowalski  and
William F. Sawin
Emmanuel Kowalski
Affiliation:
ETH Zürich – D-MATH, Rämistrasse 101, CH-8092 Zürich, Switzerland email kowalski@math.ethz.ch
William F. Sawin
Affiliation:
Princeton University, Fine Hall, Washington Road, NJ, USA email wsawin@math.princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the distribution of the polygonal paths joining partial sums of classical Kloosterman sums 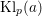$\text{Kl}_{p}(a)$, as $a$ varies over 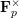$\mathbf{F}_{p}^{\times }$ and as 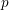$p$ tends to infinity. Using independence of Kloosterman sheaves, we prove convergence in the sense of finite distributions to a specific random Fourier series. We also consider Birch sums, for which we can establish convergence in law in the space of continuous functions. We then derive some applications.

Keywords

Kloosterman sumsKloosterman sheavesRiemann Hypothesis over finite fieldsrandom Fourier seriesshort exponential sumsprobability in Banach spaces

MSC classification

Primary: 11T23: Exponential sums 11L05: Gauss and Kloosterman sums; generalizations 14F20: Étale and other Grothendieck topologies and (co)homologies 60F17: Functional limit theorems; invariance principles 60G17: Sample path properties
Secondary: 60G50: Sums of independent random variables; random walks

Information

Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 7 , July 2016 , pp. 1489 - 1516
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bagchi, B., Statistical behaviour and universality properties of the Riemann zeta function and other allied Dirichlet series, PhD thesis, Indian Statistical Institute, Kolkata (1981), available at library.isical.ac.in/jspui/handle/10263/4256.Google Scholar
Billingsley, P., Convergence of probability measures, second edition (Wiley, 1999).Google Scholar
Birch, B. J., How the number of points of an elliptic curve over a fixed prime field varies , J. Lond. Math. Soc. (2) 43 (1968), 57–60.Google Scholar
Bober, J. W. and Goldmakher, L., The distribution of the maximum of character sums , Mathematika 59 (2013), 427–442.CrossRefGoogle Scholar
Bober, J. W., Goldmakher, L., Granville, A. and Koukoulopoulos, D., The frequency and the structure of large character sums, Preprint (2014), arXiv:1410.8189.Google Scholar
Bourgain, J. and Garaev, M. Z., Sumsets of reciprocals in prime fields and multilinear Kloosterman sums , Izv. Math. 78 (2014), 656–707.Google Scholar
Cellarosi, F. and Marklof, J., Quadratic Weyl sums, automorphic functions and invariance principles, Preprint (2015), arXiv:1501.07661.Google Scholar
Dekking, F. M. and Mendès France, M., Uniform distribution modulo one: a geometrical viewpoint , J. reine angew. Math. 329 (1981), 143–153.Google Scholar
Deligne, P., La conjecture de Weil, II , Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Deshouillers, J.-M., Geometric aspects of Weyl sums , in Elementary and analytic theory of numbers, Banach Center Publications, vol. 17 (PWN-Polish Scientific Publisher, Warsaw, 1985), 75–82.Google Scholar
Dilworth, S. J. and Montgomery-Smith, S. J., The distribution of vector-valued Rademacher series , Ann. Probab. 21 (1993), 2046–2052.Google Scholar
Fouvry, É., Kowalski, E. and Michel, Ph., A study in sums of products , Philos. Trans. R. Soc. Lond. A 373 (2015), 20140309.Google Scholar
Fouvry, É. and Michel, Ph., Sur certaines sommes d’exponentielles sur les nombres premiers , Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 93–130.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Extreme values of 𝜁(1 + it) , in The Riemann zeta function and related themes: papers in honor of Professor K. Ramachandra, Ramanujan Mathematical Society Lecture Notes Series, vol. 2 (Ramanujan Mathematical Society, India, 2006), 65–80.Google Scholar
Granville, A. and Soundararajan, K., Large character sums: pretentious characters and the Pólya–Vinogradov theorem , J. Amer. Math. Soc. 20 (2007), 357–384.Google Scholar
Holmstedt, T., Interpolation of quasi-normed spaces , Math. Scand. 26 (1970), 177–199.Google Scholar
Irving, A. J., The divisor function in arithmetic progressions to smooth moduli , Int. Math. Res. Not. IMRN 2015 (2015), 6675–6698, doi:10.1093/imrn/rnu149.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Kahane, J.-P., Some random series of functions, Cambridge Studies in Pure Mathematics, vol. 5 (Cambridge University Press, 1985).Google Scholar
Katz, N. M., On the monodromy attached to certain families of exponential sums , Duke Math. J. 54 (1987), 41–56.Google Scholar
Katz, N. M., Gauss sums, Kloosterman sums and monodromy groups, Annals of Mathematical Studies, vol. 116 (Princeton University Press, 1988).Google Scholar
Katz, N. M., Exponential sums and differential equations, Annals of Mathematical Studies, vol. 124 (Princeton University Press, 1990).Google Scholar
Katz, N. M., Convolution and equidistribution: Sato–Tate theorems for finite field Mellin transforms, Annals of Mathematical Studies, vol. 180 (Princeton University Press, 2012).Google Scholar
Kowalski, E., The Kloostermania page, blogs.ethz.ch/kowalski/the-kloostermania-page/.Google Scholar
Ledoux, M. and Talagrand, M., Probability in Banach spaces: isoperimetry and processes , Ergeb. Math. Grenzgeb. (3), vol. 23 (Springer, 1991).Google Scholar
Lehmer, D. H., Incomplete Gauss sums , Mathematika 23 (1976), 125–135.Google Scholar
Livné, R., The average distribution of cubic exponential sums , J. reine angew. Math. 375–376 (1987), 362–379.Google Scholar
Loxton, J. H., The graphs of exponential sums , Mathematika 30 (1983), 153–163.Google Scholar
Loxton, J. H., The distribution of exponential sums , Mathematika 32 (1985), 16–25.Google Scholar
Montgomery, H. and Odlyzko, A., Large deviations of sums of independent random variables , Acta Arith. 49 (1988), 427–434.Google Scholar
Montgomery-Smith, S. J., The distribution of Rademacher sums , Proc. Amer. Math. Soc. 109 (1990), 517–522.Google Scholar
Revuz, D. and Yor, M., Continuous Martingales and Brownian motion, third edition (Springer, Berlin, 1999).Google Scholar
Sawin, W. F., A Tannakian category of arithmetic exponential sums, PhD thesis, Princeton University (2016).Google Scholar
Talagrand, M., Concentration of measure and isoperimetric inequalities in product spaces , Publ. Math. Inst. Hautes Études Sci. 81 (1995), 73–205.Google Scholar