Published online by Cambridge University Press: 05 September 2022
We prove that any nef 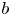 $b$-divisor class on a projective variety defined over an algebraically closed field of characteristic zero is a decreasing limit of nef Cartier classes. Building on this technical result, we construct an intersection theory of nef
$b$-divisor class on a projective variety defined over an algebraically closed field of characteristic zero is a decreasing limit of nef Cartier classes. Building on this technical result, we construct an intersection theory of nef 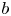 $b$-divisors, and prove several variants of the Hodge index theorem inspired by the work of Dinh and Sibony. We show that any big and basepoint-free curve class is a power of a nef
$b$-divisors, and prove several variants of the Hodge index theorem inspired by the work of Dinh and Sibony. We show that any big and basepoint-free curve class is a power of a nef 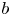 $b$-divisor, and relate this statement to the Zariski decomposition of curves classes introduced by Lehmann and Xiao. Our construction allows us to relate various Banach spaces contained in the space of
$b$-divisor, and relate this statement to the Zariski decomposition of curves classes introduced by Lehmann and Xiao. Our construction allows us to relate various Banach spaces contained in the space of 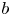 $b$-divisors which were defined in our previous work.
$b$-divisors which were defined in our previous work.