Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T01:01:55.395Z Has data issue: false hasContentIssue false
  • English
  • Français

Homological mirror symmetry for higher-dimensional pairs of pants

Part of: Symplectic geometry, contact geometry Surfaces and higher-dimensional varieties (Co)homology theory

Published online by Cambridge University Press:  18 June 2020

Yankı Lekili  and
Alexander Polishchuk
Yankı Lekili
Affiliation:
King’s College London, LondonWC2R 2LS, UK email yanki.lekili@kcl.ac.uk
Alexander Polishchuk
Affiliation:
University of Oregon, National Research University Higher School of Economics, USA Korea Institute for Advanced Study, South Korea email apolish@uoregon.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

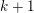Using Auroux’s description of Fukaya categories of symmetric products of punctured surfaces, we compute the partially wrapped Fukaya category of the complement of $k+1$ generic hyperplanes in 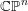$\mathbb{CP}^{n}$, for 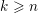$k\geqslant n$, with respect to certain stops in terms of the endomorphism algebra of a generating set of objects. The stops are chosen so that the resulting algebra is formal. In the case of the complement of 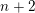$n+2$ generic hyperplanes in 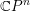$\mathbb{C}P^{n}$ ($n$-dimensional pair of pants), we show that our partial wrapped Fukaya category is equivalent to a certain categorical resolution of the derived category of the singular affine variety 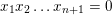$x_{1}x_{2}\ldots x_{n+1}=0$. By localizing, we deduce that the (fully) wrapped Fukaya category of the $n$-dimensional pair of pants is equivalent to the derived category of 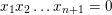$x_{1}x_{2}\ldots x_{n+1}=0$. We also prove similar equivalences for finite abelian covers of the $n$-dimensional pair of pants.

Keywords

homological mirror symmetrypartially wrapped Fukaya categorysymmetric products of surfaceshigher-dimensional pairs of pantsmodules over non-commutative orders

MSC classification

Primary: 14J33: Mirror symmetry
Secondary: 14F05: Sheaves, derived categories of sheaves and related constructions 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 7 , July 2020 , pp. 1310 - 1347
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abouzaid, M. and Seidel, P., An open string analogue of Viterbo functoriality, Geom. Topol. 14 (2010), 627–718.10.2140/gt.2010.14.627CrossRefGoogle Scholar
Auroux, D., Fukaya categories of symmetric products and bordered Heegaard–Floer homology, J. Gökova Geom. Topol. GGT 4 (2010), 1–54.Google Scholar
Auroux, D., Fukaya categories and bordered Heegaard–Floer homology, Proceedings of the International Congress of Mathematicians, vol. II (Hindustan Book Agency, New Delhi, 2010), 917–941.Google Scholar
Auroux, D., Speculations on homological mirror symmetry for hypersurfaces in ℂ×, Survey in Differential Geometry, vol. 22 (International Press, Somerville, MA, 2018), 1–47.Google Scholar
Bondal, A., Larsen, M. and Lunts, V., Grothendieck ring of pretriangulated categories, Int. Math. Res. Not. IMRN 2004 (2004), 1461–1495.10.1155/S1073792804140385CrossRefGoogle Scholar
Burban, I. and Drozd, Y., Tilting on non-commutative rational projective curves, Math. Ann. 351 (2011), 665–709.10.1007/s00208-010-0585-4CrossRefGoogle Scholar
Dao, H., Faber, E. and Ingalls, C., Noncommutative (crepant) desingularizations and the global spectrum of commutative rings, Algebr. Represent. Theory 18 (2015), 633–664.10.1007/s10468-014-9510-yCrossRefGoogle Scholar
Gammage, B. and Nadler, D., Mirror symmetry for honeycombs, Trans. Amer. Math. Soc. 373 (2020), 71–107.10.1090/tran/7909CrossRefGoogle Scholar
Ganatra, S., Symplectic cohomology and duality for the wrapped Fukaya category, PhD thesis, Massachusetts Institute of Technology (2012). Preprint (2013), arXiv:1304.7312v1.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., Structural results in wrapped Floer theory, Preprint (2018), arXiv:1809.0342.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., Microlocal Morse theory of wrapped Fukaya categories, Preprint (2018), arXiv:1809.08807.Google Scholar
Ganatra, S., Pardon, J. and Shende, V., Covariantly functorial wrapped Floer theory on Liouville sectors, Publ. Math. Inst. Hautes Études Sci. (2019), to appear. Preprint (2017), arXiv:1706.03152.Google Scholar
Haiden, F., Katzarkov, L. and Kontsevich, M., Flat surfaces and stability structures, Publ. Math. Inst. Hautes Études Sci. 126 (2017), 247–318.CrossRefGoogle Scholar
Isik, M. U., Equivalence of the derived category of a variety with a singularity category, Int. Math. Res. Not. IMRN 2013 (2013), 2787–2808.10.1093/imrn/rns125CrossRefGoogle Scholar
Kuznetsov, A. and Lunts, V., Categorical resolutions of irrational singularities, Int. Math. Res. Not. IMRN 2015 (2015), 4536–4625.10.1093/imrn/rnu072CrossRefGoogle Scholar
Lekili, Y. and Perutz, T., Fukaya categories of the torus and Dehn surgery, Proc. Natl. Acad. Sci. USA 108 (2011), 8106–8113.10.1073/pnas.1018918108CrossRefGoogle ScholarPubMed
Lekili, Y. and Polishchuk, A., Auslander orders over nodal stacky curves and partially wrapped Fukaya categories, J. Topol. 11 (2018), 615–644.CrossRefGoogle Scholar
Lekili, Y. and Polishchuk, A., Derived equivalences of gentle algebras via Fukaya categories, Math. Ann. 376 (2020), 187–225.CrossRefGoogle Scholar
Lekili, Y. and Ueda, K., Homological mirror symmetry for K3 surfaces via moduli of $A_{\infty }$-structures, Preprint (2018), arXiv:1806.04345.Google Scholar
Lipshitz, R., Ozsváth, P. and Thurston, D., Bordered Heegaard–Floer homology, Mem. Amer. Math. Soc. 254 (2018).Google Scholar
Lunts, V., Categorical resolution of singularities, J. Algebra 323 (2010), 2977–3003.10.1016/j.jalgebra.2009.12.023CrossRefGoogle Scholar
Mikhalkin, G., Decomposition into pairs-of-pants for complex algebraic hypersurfaces, Topology 43 (2004), 1035–1065.CrossRefGoogle Scholar
Miyachi, J. I., Localization of triangulated categories and derived categories, J. Algebra 141 (1991), 463–483.CrossRefGoogle Scholar
Nadler, D., Wrapped microlocal sheaves on pairs of pants, Preprint (2016), arXiv:1604.00114.Google Scholar
Orlov, D., Triangulated categories of singularities and D-branes in Landau–Ginzburg models, Proc. Steklov Inst. Math. 246 (2004), 227–248.Google Scholar
Ozsváth, P. and Szabó, Z., Kauffman states, bordered algebras and a bigraded knot invariant, Adv. Math. 328 (2018), 1088–1198.10.1016/j.aim.2018.02.017CrossRefGoogle Scholar
Perutz, T., Hamiltonian handleslides for Heegaard Floer homology, in Proceedings of Gökova Geometry-Topology Conference 2007 (Gökova Geometry/Topology Conference (GGT), Gökova, 2008), 15–35.Google Scholar
Seidel, P., Graded Lagrangian submanifolds, Bull. Soc. Math. France 128 (2000), 103–149.10.24033/bsmf.2365CrossRefGoogle Scholar
Seidel, P., Fukaya categories and Picard–Lefschetz theory, Zurich Lectures in Advanced Mathematics (European Mathematical Society (EMS), Zürich, 2008).10.4171/063CrossRefGoogle Scholar
Seidel, P., Homological mirror symmetry for the quartic surface, Mem. Amer. Math. Soc. 236 (2015).Google Scholar
Sheridan, N., On the homological mirror symmetry conjecture for pairs of pants, J. Differential Geom. 89 (2011), 271–367.CrossRefGoogle Scholar
Shipman, I., A geometric approach to Orlov’s theorem, Compos. Math. 148 (2012), 1365–1389.CrossRefGoogle Scholar
Toën, B. and Vaquié, M., Moduli of objects in dg-categories, Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 387–444.CrossRefGoogle Scholar