Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hagen, Mark F.
2014.
Cocompactly cubulated crystallographic groups.
Journal of the London Mathematical Society,
Vol. 90,
Issue. 1,
p.
140.
Wise, Daniel
2014.
Cubular tubular groups.
Transactions of the American Mathematical Society,
Vol. 366,
Issue. 10,
p.
5503.
Hagen, Mark F.
and
Przytycki, Piotr
2015.
Cocompactly cubulated graph manifolds.
Israel Journal of Mathematics,
Vol. 207,
Issue. 1,
p.
377.
Hsu, Tim
and
Wise, Daniel T.
2015.
Cubulating malnormal amalgams.
Inventiones mathematicae,
Vol. 199,
Issue. 2,
p.
293.
Hagen, Mark F.
and
Wise, Daniel T.
2015.
Cubulating hyperbolic free-by-cyclic groups: the general case.
Geometric and Functional Analysis,
Vol. 25,
Issue. 1,
p.
134.
Woodhouse, Daniel J.
2016.
Classifying finite dimensional cubulations of tubular groups.
Michigan Mathematical Journal,
Vol. 65,
Issue. 3,
Hagen, Mark F.
and
Wise, Daniel T.
2016.
Cubulating hyperbolic free-by-cyclic groups: The irreducible case.
Duke Mathematical Journal,
Vol. 165,
Issue. 9,
Przytycki, Piotr
and
Wise, Daniel
2017.
Mixed 3-manifolds are virtually special.
Journal of the American Mathematical Society,
Vol. 31,
Issue. 2,
p.
319.
Wise, Daniel T.
and
Woodhouse, Daniel J.
2017.
A cubical flat torus theorem and the bounded packing property.
Israel Journal of Mathematics,
Vol. 217,
Issue. 1,
p.
263.
Huang, Jingyin
and
Kleiner, Bruce
2018.
Groups quasi-isometric to right-angled Artin groups.
Duke Mathematical Journal,
Vol. 167,
Issue. 3,
Cooper, Daryl
and
Futer, David
2019.
Ubiquitous quasi-Fuchsian surfaces in cusped hyperbolic 3–manifolds.
Geometry & Topology,
Vol. 23,
Issue. 1,
p.
241.
Einstein, Eduard
and
Groves, Daniel
2020.
Relative cubulations and groups with a 2-sphere boundary.
Compositio Mathematica,
Vol. 156,
Issue. 4,
p.
862.
Behrstock, Jason
Hagen, Mark F.
and
Sisto, Alessandro
2021.
Quasiflats in hierarchically hyperbolic spaces.
Duke Mathematical Journal,
Vol. 170,
Issue. 5,
Fioravanti, Elia
and
Hagen, Mark
2021.
Deforming cubulations of hyperbolic groups.
Journal of Topology,
Vol. 14,
Issue. 3,
p.
877.
Einstein, Eduard
and
Groves, Daniel
2022.
Relatively geometric actions on CAT$\operatorname{CAT}$(0) cube complexes.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 1,
p.
691.
Petrosyan, Nansen
2022.
Decomposing groups by codimension-1 subgroups.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 11,
p.
4587.
Groves, Daniel
and
Manning, Jason Fox
2022.
Specializing cubulated relatively hyperbolic groups.
Journal of Topology,
Vol. 15,
Issue. 2,
p.
398.
Groves, Daniel
and
Manning, Jason Fox
2023.
Hyperbolic groups acting improperly.
Geometry & Topology,
Vol. 27,
Issue. 9,
p.
3387.
Haulmark, Matthew
and
Hruska, G. Christopher
2023.
On canonical splittings of relatively hyperbolic groups.
Israel Journal of Mathematics,
Vol. 258,
Issue. 1,
p.
249.
Hagen, Mark F
and
Petyt, Harry
2023.
Projection complexes and quasimedian maps.
Algebraic & Geometric Topology,
Vol. 22,
Issue. 7,
p.
3277.
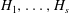 $H_1,\ldots, H_s$ be relatively quasiconvex codimension-1 subgroups of a group
$H_1,\ldots, H_s$ be relatively quasiconvex codimension-1 subgroups of a group 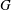 $G$ that is hyperbolic relative to
$G$ that is hyperbolic relative to 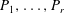 $P_1, \ldots, P_r$. We prove that
$P_1, \ldots, P_r$. We prove that 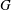 $G$ acts relatively cocompactly on the associated dual CAT(0) cube complex
$G$ acts relatively cocompactly on the associated dual CAT(0) cube complex 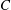 $C$. This generalizes Sageev’s result that
$C$. This generalizes Sageev’s result that 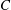 $C$ is cocompact when
$C$ is cocompact when 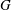 $G$ is hyperbolic. When
$G$ is hyperbolic. When 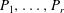 $P_1,\ldots, P_r$ are abelian, we show that the dual CAT(0) cube complex
$P_1,\ldots, P_r$ are abelian, we show that the dual CAT(0) cube complex 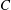 $C$ has a
$C$ has a 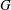 $G$-cocompact CAT(0) truncation.
$G$-cocompact CAT(0) truncation.