Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-29T19:52:05.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Central limit theorems for counting measures in coarse negative curvature

Part of: Limit theorems Low-dimensional topology Special aspects of infinite or finite groups

Published online by Cambridge University Press:  03 November 2022

Ilya Gekhtman ,
Samuel J. Taylor  and
Giulio Tiozzo
Ilya Gekhtman
Affiliation:
Faculty of Mathematics, Technion-Israel Institute of Technology, Haifa 3200003, Israelilyagekh@gmail.com
Samuel J. Taylor
Affiliation:
Department of Mathematics, Temple University, 1805 North Broad Street, Philadelphia, PA 19122, USA samuel.taylor@temple.edu
Giulio Tiozzo
Affiliation:
Department of Mathematics, University of Toronto, 40 St George St, Toronto, ON M5S 2E4, Canada tiozzo@math.toronto.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish central limit theorems for an action of a group 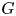$G$ on a hyperbolic space 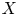$X$ with respect to the counting measure on a Cayley graph of 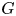$G$. Our techniques allow us to remove the usual assumptions of properness and smoothness of the space, or cocompactness of the action. We provide several applications which require our general framework, including to lengths of geodesics in geometrically finite manifolds and to intersection numbers with submanifolds.

Keywords

central limit theoremhyperbolic spacesgroup actionsdisplacementtranslation lengthcounting measurerandom walk

MSC classification

Primary: 60F05: Central limit and other weak theorems 57M60: Group actions in low dimensions 20F67: Hyperbolic groups and nonpositively curved groups

Information

Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 10 , October 2022 , pp. 1980 - 2013
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Gekhtman is partially supported by NSERC. Taylor is partially supported by NSF grants DMS-1744551, DMS-2102018 and the Sloan Foundation. Tiozzo is partially supported by NSERC, an Ontario Early Researcher Award and the Sloan Foundation.

References

Agol, I., Tameness of hyperbolic 3-manifolds, Preprint (2004), arXiv:math/0405568.Google Scholar
Antolin, Y. and Ciobanu, L., Finite generating sets of relatively hyperbolic groups and applications to geodesic languages, Trans. Amer. Math. Soc. 368 (2016), 7965–8010.CrossRefGoogle Scholar
Arzhantseva, G. N. and Lysenok, I. G., Growth tightness for word hyperbolic groups, Math. Z. 241 (2002), 597–611.CrossRefGoogle Scholar
Bader, U. and Furman, A., Some ergodic properties of metrics on hyperbolic groups, Preprint (2017), arXiv:1707.02020.Google Scholar
Benoist, Y. and Quint, J.-F., Central limit theorem on hyperbolic groups, Izv. Math. 80 (2016), 3–23.CrossRefGoogle Scholar
Björklund, M. and Hartnick, T., Biharmonic functions on groups and limit theorems for quasimorphisms along random walks, Geom. Topol. 15 (2011), 123–143.CrossRefGoogle Scholar
Bowen, R., Equilibrium states and the ergodic theory of Anosov diffeomorphisms, Lecture Notes in Mathematics, vol. 470 (Springer, 1975).CrossRefGoogle Scholar
Calegari, D. and Fujiwara, K., Combable functions, quasimorphisms, and the central limit theorem, Ergodic Theory Dynam. Systems 30 (2010), 1343–1369.CrossRefGoogle Scholar
Calegari, D. and Gabai, D., Shrinkwrapping and the taming of hyperbolic 3-manifolds, J. Amer. Math. Soc. 19 (2006), 385–446.CrossRefGoogle Scholar
Cannon, J. W., The combinatorial structure of cocompact discrete hyperbolic groups, Geom. Dedicata 16 (1984), 123–148.CrossRefGoogle Scholar
Cantrell, S., Statistical limit laws for hyperbolic groups, Trans. Amer. Math. Soc. 374 (2021), 2687–2732.CrossRefGoogle Scholar
Chas, M. and Lalley, S. P., Self-intersections in combinatorial topology: statistical structure, Invent. Math. 188 (2012), 429–463.CrossRefGoogle Scholar
Chas, M., Li, K. and Maskit, B., Experiments suggesting that the distribution of the hyperbolic length of closed geodesics sampling by word length is Gaussian, Exp. Math. 22 (2013), 367–371.CrossRefGoogle Scholar
Coornaert, M., Mesures de Patterson-Sullivan sur le bord d'un espace hyperbolique au sens de Gromov, Pacific J. Math. 159 (1993), 241–270.CrossRefGoogle Scholar
Coulon, R., Dougall, R., Schapira, B. and Tapie, S., Twisted Patterson-Sullivan measures and applications to amenability and coverings, Mem. Amer. Math. Soc., to appear. Preprint (2018), arXiv:1809.10881.Google Scholar
Epstein, D., Paterson, M. S., Cannon, J. W., Holt, D. F., Levy, S. V. and Thurston, W. P., Word processing in groups (AK Peters, 1992).CrossRefGoogle Scholar
Furman, A., Coarse-geometric perspective on negatively curved manifolds and groups, in Rigidity in dynamics and geometry (Cambridge, 2000) (Springer, Berlin, 2002), 149–166.CrossRefGoogle Scholar
Furstenberg, H., Noncommuting random products, Trans. Amer. Math. Soc. 108 (1963), 377–428.CrossRefGoogle Scholar
Gekhtman, I., Taylor, S. J. and Tiozzo, G., Counting loxodromics for hyperbolic actions, J. Topol. 11 (2018), 379–419.CrossRefGoogle Scholar
Gekhtman, I., Taylor, S. J. and Tiozzo, G., A central limit theorem for closed geodesics: proof of the Chas-Li-Maskit conjecture, Adv. Math. 358 (2019), 106852.CrossRefGoogle Scholar
Gekhtman, I., Taylor, S. J. and Tiozzo, G., Counting problems in graph products and relatively hyperbolic groups, Israel J. Math. 237 (2020), 311–371.CrossRefGoogle Scholar
Gekhtman, I. and Tiozzo, G., Entropy and drift for Gibbs measures on geometrically finite manifolds, Trans. Amer. Math. Soc. 373 (2020), 2949–2980.CrossRefGoogle Scholar
Gouëzel, S., Mathéus, F. and Maucourant, F., Entropy and drift in word hyperbolic groups, Invent. Math. 211 (2018), 1201–1255.CrossRefGoogle Scholar
Guivarc'h, Y. and Raugi, A., Products of random matrices: convergence theorem, Contemp. Math. 50 (1986), 31–53.CrossRefGoogle Scholar
Hermiller, S. and Meier, J., Algorithms and geometry for graph products of groups, J. Algebra 171 (1995), 230–257.CrossRefGoogle Scholar
Holt, D. F., Rees, S. and Röver, C. E., Groups, languages and automata, London Mathematical Society Student Texts, vol. 88 (Cambridge University Press, Cambridge, 2017).CrossRefGoogle Scholar
Horbez, C., Central limit theorems for mapping class groups and $Out(F_N)$, Geom. Topol. 22 (2018), 105–156.CrossRefGoogle Scholar
Horsham, M. and Sharp, R., Lengths, quasi-morphisms and statistics for free groups, Contemp. Math. 14 (2009), 219–237.CrossRefGoogle Scholar
Kac, M., On the notion of recurrence in discrete stochastic processes, Bull. Amer. Math. Soc. 53 (1947), 1002–1010.CrossRefGoogle Scholar
Kapovich, M., Hyperbolic manifolds and discrete groups, vol. 183 (Springer, 2001).Google Scholar
Kim, I., Length spectrum in rank-1 symmetric spaces is not arithmetic, Proc. Amer. Math. Soc. 134 (2006), 3691–3696.CrossRefGoogle Scholar
Lalley, S. P., Distribution of periodic orbits of symbolic and Axiom A flows, Adv. Appl. Math. 8 (1987), 154–193.CrossRefGoogle Scholar
Maher, J. and Tiozzo, G., Random walks on weakly hyperbolic groups, J. Reine Angew. Math. 742 (2018), 187–239.CrossRefGoogle Scholar
Mathieu, P. and Sisto, A., Deviation inequalities for random walks, Duke Math. J. 169 (2020), 961–1036.CrossRefGoogle Scholar
Melbourne, I. and Török, A., Statistical limit theorems for suspension flows, Israel J. Math. 144 (2004), 191–209.CrossRefGoogle Scholar
Morita, T., Deterministic version lemmas in ergodic theory of random dynamical systems, Hiroshima Math. J. 18 (1988), 15–29.CrossRefGoogle Scholar
Mosher, L., Central quotients of biautomatic group, Comment. Math. Helv. 72 (1997), 16–29.CrossRefGoogle Scholar
Parry, W., Intrinsic Markov chains, Trans. Amer. Math. Soc. 112 (1964), 55–66.CrossRefGoogle Scholar
Parry, W. and Pollicott, M., Zeta functions and the periodic orbit structure of hyperbolic dynamics, Astérisque 187–188 (1990).Google Scholar
Pollicott, M. and Sharp, R., Comparison theorems and orbit counting in hyperbolic geometry, Trans. Amer. Math. Soc. 350 (1998), 473–499.CrossRefGoogle Scholar
Pollicott, M. and Sharp, R., Poincaré series and comparison theorems for variable negative curvature, in Topology, ergodic theory, real algebraic geometry, American Mathematical Society Translations: Series 2, vol. 202 (American Mathematical Society, Providence, RI, 2001), 229–240.Google Scholar
Pollicott, M. and Sharp, R., Correlations for pairs of closed geodesics, Invent. Math. 163 (2006), 1–24.CrossRefGoogle Scholar
Ratner, M., The central limit theorem for geodesic flows on $n$-dimensional manifolds of negative curvature, Israel J. Math. 16 (1973), 181–197.CrossRefGoogle Scholar
Rivin, I., Growth in free groups (and other stories)—twelve years later, Illinois J. Math. 54 (2010), 327–370.CrossRefGoogle Scholar
Ruelle, D., Thermodynamic formalism (Cambridge University Press, 2004).CrossRefGoogle Scholar
Sarig, O., Lecture notes on ergodic theory, Preprint (2020), available online at http://www.weizmann.ac.il/math/sarigo/sites/math.sarigo/files/uploads/ergodicnotes.pdf.Google Scholar
Scott, P. and Wall, T., Topological methods in group theory, in Homological group theory, London Mathematical Society Lecture Note series, vol. 36 (Cambridge University Press, 1979), 137–203.CrossRefGoogle Scholar
Shalen, P., Representations of 3-manifold groups, in Handbook of geometric topology, eds Daverman, R. and Sher, R. (North-Holland, Amsterdam, 2002), 955–1044.Google Scholar
Sinai, Y. G., The central limit theorem for geodesic flows on manifolds of constant negative curvature, Soviet Math. Dokl. 1 (1960), 938–987.Google Scholar
Sinai, Y. G., Gibbs measures in ergodic theory, Uspekhi Mat. Nauk 27 (1972), 21–64.Google Scholar
Walters, P., An introduction to ergodic theory, Graduate Texts in Mathematics, vol. 79 (Springer, 2000).Google Scholar
Yang, W. Y., Statistically convex-cocompact actions of groups with contracting elements, Int. Math. Res. Not. IMRN 2019 (2019), 7259–7323.CrossRefGoogle Scholar