Article contents
The Baum–Connes conjecture localised at the unit element of a discrete group
Published online by Cambridge University Press: 14 January 2021
Abstract
We construct a Baum–Connes assembly map localised at the unit element of a discrete group 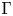 $\Gamma$. This morphism, called
$\Gamma$. This morphism, called 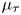 $\mu _\tau$, is defined in
$\mu _\tau$, is defined in 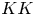 $KK$-theory with coefficients in
$KK$-theory with coefficients in 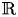 $\mathbb {R}$ by means of the action of the idempotent
$\mathbb {R}$ by means of the action of the idempotent 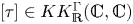 $[\tau ]\in KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ canonically associated to the group trace of
$[\tau ]\in KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ canonically associated to the group trace of 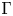 $\Gamma$. We show that the corresponding
$\Gamma$. We show that the corresponding 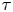 $\tau$-Baum–Connes conjecture is weaker than the classical version, but still implies the strong Novikov conjecture. The right-hand side of
$\tau$-Baum–Connes conjecture is weaker than the classical version, but still implies the strong Novikov conjecture. The right-hand side of 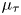 $\mu _\tau$ is functorial with respect to the group
$\mu _\tau$ is functorial with respect to the group 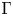 $\Gamma$.
$\Gamma$.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2021
Footnotes
Paolo Antonini was partially supported by the grant H2020-MSCA-RISE-2015-691246-QUANTUM DYNAMICS; Sara Azzali acknowledges support by the DFG grant Secondary invariants for foliations within the Priority Programme SPP 2026 ‘Geometry at Infinity’.
References
- 3
- Cited by


