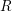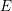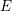Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vogt, Isabel
2019.
Abelian varieties isogenous to a power of an elliptic curve over a Galois extension.
Journal de théorie des nombres de Bordeaux,
Vol. 31,
Issue. 1,
p.
205.
Marseglia, Stefano
2019.
Computing abelian varieties over finite fields isogenous to a power.
Research in Number Theory,
Vol. 5,
Issue. 4,
Kirschmer, Markus
Narbonne, Fabien
Ritzenthaler, Christophe
and
Robert, Damien
2021.
Spanning the isogeny class of a power of an elliptic curve.
Mathematics of Computation,
Vol. 91,
Issue. 333,
p.
401.
Xue, Jiang Wei
and
Yu, Chia Fu
2021.
On Counting Certain Abelian Varieties Over Finite Fields.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 1,
p.
205.
Marseglia, Stefano
2022.
Computing base extensions of ordinary abelian varieties over finite fields.
International Journal of Number Theory,
Vol. 18,
Issue. 09,
p.
1957.
Centeleghe, Tommaso Giorgio
and
Stix, Jakob
2023.
Categories of abelian varieties over finite fields II: Abelian varieties over $${\mathbb{F}_q}$$ and Morita equivalence.
Israel Journal of Mathematics,
Vol. 257,
Issue. 1,
p.
103.
Laga, Jef
Schembri, Ciaran
Shnidman, Ari
and
Voight, John
2024.
Rational torsion points on abelian surfaces with quaternionic multiplication.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
Ibukiyama, Tomoyoshi
Karemaker, Valentijn
and
Yu, Chia-Fu
2025.
When is a polarised abelian variety determined by its 𝑝-divisible group?.
Transactions of the American Mathematical Society, Series B,
Vol. 12,
Issue. 3,
p.
65.
Robert, Damien
2025.
Number-Theoretic Methods in Cryptology.
Vol. 14966,
Issue. ,
p.
3.
Galbraith, Steven D.
Gilchrist, Valerie
and
Robert, Damien
2026.
Progress in Cryptology – LATINCRYPT 2025.
Vol. 16129,
Issue. ,
p.
174.