Article contents
Simplex Stability
Published online by Cambridge University Press: 01 May 2009
Abstract
A d-simplex is a collection of d + 1 sets such that every d of them has non-empty intersection and the intersection of all of them is empty. Fix k ≥ d + 2 ≥ 3 and let 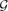 be a family of k-element subsets of an n-element set that contains no d-simplex. We prove that if
be a family of k-element subsets of an n-element set that contains no d-simplex. We prove that if 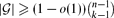 , then there is a vertex x of
, then there is a vertex x of 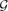 such that the number of sets in
such that the number of sets in 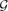 omitting x is o(nk−1) (here o(1)→ 0 and n → ∞). A similar result when n/k is bounded from above was recently proved in [10].
omitting x is o(nk−1) (here o(1)→ 0 and n → ∞). A similar result when n/k is bounded from above was recently proved in [10].
Our main result is actually stronger, and implies that if 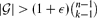 for any ϵ < 0 and n sufficiently large, then
for any ϵ < 0 and n sufficiently large, then 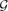 contains d + 2 sets A, A1, . . . ,Ad+1 such that the Ais form a d-simplex, and A contains an element of ∩j≠iAj for each i. This generalizes, in asymptotic form, a recent result of Vestraëte and the first author [18], who proved it for d = 1, ϵ = 0 and n ≥ 2k.
contains d + 2 sets A, A1, . . . ,Ad+1 such that the Ais form a d-simplex, and A contains an element of ∩j≠iAj for each i. This generalizes, in asymptotic form, a recent result of Vestraëte and the first author [18], who proved it for d = 1, ϵ = 0 and n ≥ 2k.
Information
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2009
References
- 7
- Cited by

