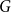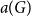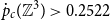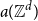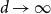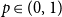1. Introduction
We improve on the best known asymptotic bounds on the exponential growth rates
![]() $a({\mathbb{Z}}^d)$
of lattice animals as
$a({\mathbb{Z}}^d)$
of lattice animals as
![]() $d\to \infty$
, using a probabilistic method involving percolation theory. Along the way we also obtain new results on percolation.
$d\to \infty$
, using a probabilistic method involving percolation theory. Along the way we also obtain new results on percolation.
1.1. Lattice animals
A lattice animal is a connected subgraph
![]() $S$
of the hypercubic lattice
$S$
of the hypercubic lattice
![]() ${\mathbb{Z}}^d$
or more generally of a vertex-transitive graph
${\mathbb{Z}}^d$
or more generally of a vertex-transitive graph
![]() $G$
. The counts of lattice animals with prescribed parameters have been extensively studied by scholars in statistical mechanics as well as combinatorics and computer science [Reference Barequet, Barequet and Rote4, Reference Barequet and Shalah6, Reference Delyon11, Reference Gaunt and Peard15, Reference Hammond19, Reference Harris22, Reference Miranda and Slade36–Reference Peard and Gaunt38], both in
$G$
. The counts of lattice animals with prescribed parameters have been extensively studied by scholars in statistical mechanics as well as combinatorics and computer science [Reference Barequet, Barequet and Rote4, Reference Barequet and Shalah6, Reference Delyon11, Reference Gaunt and Peard15, Reference Hammond19, Reference Harris22, Reference Miranda and Slade36–Reference Peard and Gaunt38], both in
![]() ${\mathbb{Z}}^d$
and other lattices [Reference Barequet, Rote and Shalah5, Reference Barequet, Shalah and Zheng7, Reference Rands and Welsh39]. A lot of the motivation comes from the study of random configurations in
${\mathbb{Z}}^d$
and other lattices [Reference Barequet, Rote and Shalah5, Reference Barequet, Shalah and Zheng7, Reference Rands and Welsh39]. A lot of the motivation comes from the study of random configurations in
![]() ${\mathbb{Z}}^d$
, the central theme in many models of statistical mechanics. Our focus is Bernoulli (bond or site) percolation. Given a value of the percolation parameter
${\mathbb{Z}}^d$
, the central theme in many models of statistical mechanics. Our focus is Bernoulli (bond or site) percolation. Given a value of the percolation parameter
![]() $p\in [0,1]$
, we can express the probability
$p\in [0,1]$
, we can express the probability
![]() $\theta (p)$
that the cluster
$\theta (p)$
that the cluster
![]() $C_o$
of the origin
$C_o$
of the origin
![]() $o$
is infinite as
$o$
is infinite as
The probability
![]() ${\mathbb{P}}_p(C_o=A)$
is easily expressed as
${\mathbb{P}}_p(C_o=A)$
is easily expressed as
![]() $p^{||A||} (1-p)^{|\partial A|}$
by the definition of bond percolation, where
$p^{||A||} (1-p)^{|\partial A|}$
by the definition of bond percolation, where
![]() $||A||$
is the number of edges in
$||A||$
is the number of edges in
![]() $A$
, and the boundary
$A$
, and the boundary
![]() $\partial A$
comprises the edges outside
$\partial A$
comprises the edges outside
![]() $A$
that are incident with
$A$
that are incident with
![]() $A$
. Thus, if we could enumerate the set of lattice animals
$A$
. Thus, if we could enumerate the set of lattice animals
![]() $A_{n,m}$
with size
$A_{n,m}$
with size
![]() $n$
and boundary size
$n$
and boundary size
![]() $m$
accurately enough, we could answer any question of percolation theory such as the continuity of
$m$
accurately enough, we could answer any question of percolation theory such as the continuity of
![]() $\theta (p)$
or the exact value of the critical threshold
$\theta (p)$
or the exact value of the critical threshold
![]() $p_c$
. In practice, however,
$p_c$
. In practice, however,
![]() $A_{n,m}$
is too difficult to enumerate, and one studies asymptotics as
$A_{n,m}$
is too difficult to enumerate, and one studies asymptotics as
![]() $n,m\to \infty$
. Such asymptotics, specifically the exponential growth rates, are still informative enough about the behaviour of percolation, and the present paper provides results in this vein.
$n,m\to \infty$
. Such asymptotics, specifically the exponential growth rates, are still informative enough about the behaviour of percolation, and the present paper provides results in this vein.
1.2. Interfaces
Certain subfamilies of lattice animals, called interfaces, have also been extensively studied either as a tool in the study of statistical mechanics or for their own sake [Reference Cerf10, Reference Dobrushin, Kotecky and Shlosman12]. The term interface is commonly used to denote the common boundary of two components of a crystal or liquid that are in a different phase. The precise meaning of the term varies according to the model in question and the perspective of its study. When studying percolation on a planar lattice
![]() $L$
for example, the interface of the cluster
$L$
for example, the interface of the cluster
![]() $C_o$
of the origin can be thought of as the minimal cut separating
$C_o$
of the origin can be thought of as the minimal cut separating
![]() $C_o$
from infinity, which forms a cycle in the dual
$C_o$
from infinity, which forms a cycle in the dual
![]() $L^*$
. Peierls’ argument [Reference Grimmett18] is a famous application of the notion that uses an upper bound on the number of such cycles to deduce an upper bound on
$L^*$
. Peierls’ argument [Reference Grimmett18] is a famous application of the notion that uses an upper bound on the number of such cycles to deduce an upper bound on
![]() $p_c(L)$
.
$p_c(L)$
.
In [Reference Georgakopoulos and Panagiotis17], we introduced a variant of the notion of interface – see Definitions 3.3 and 3.6 – and used it to prove the analyticity of the percolation density
![]() $\theta (p)$
for supercritical Bernoulli percolation on
$\theta (p)$
for supercritical Bernoulli percolation on
![]() ${\mathbb{Z}}^d$
. Our proof relied on the fact that our interfaces satisfy a generalisation of (1). Therefore, as argued above for lattice animals, counting interfaces accurately enough would yield important conclusions in percolation theory. This observation is the main motivation of this paper, which studies the exponential growth rate
${\mathbb{Z}}^d$
. Our proof relied on the fact that our interfaces satisfy a generalisation of (1). Therefore, as argued above for lattice animals, counting interfaces accurately enough would yield important conclusions in percolation theory. This observation is the main motivation of this paper, which studies the exponential growth rate
![]() $b(G)$
of interfaces of a ‘lattice’
$b(G)$
of interfaces of a ‘lattice’
![]() $G$
. Our first result is the following inequality relating
$G$
. Our first result is the following inequality relating
![]() $b(G)$
to
$b(G)$
to
![]() ${p}_c(G)$
:
${p}_c(G)$
:
where
![]() $f(r)\,:\!= \frac{(1+r)^{1+r}}{r^r}$
and
$f(r)\,:\!= \frac{(1+r)^{1+r}}{r^r}$
and
![]() $r(p)\,:\!=\frac{1-p}{p}$
are universal functions. The class
$r(p)\,:\!=\frac{1-p}{p}$
are universal functions. The class
![]() $\mathcal S$
of lattices
$\mathcal S$
of lattices
![]() $G$
we work with includes the standard cubic lattice in
$G$
we work with includes the standard cubic lattice in
![]() ${\mathbb{Z}}^d, d\geq 2$
, as well as all doubly periodic planar lattices, which include any regular tessellation of the Euclidean plane; see Section 3 for the definition of
${\mathbb{Z}}^d, d\geq 2$
, as well as all doubly periodic planar lattices, which include any regular tessellation of the Euclidean plane; see Section 3 for the definition of
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
The fact that interfaces are a subspecies of lattice animals leads to the inequality
![]() $a(G)\geq b(G)$
. Inequality (2) allows us to translate any upper bound on the percolation threshold of a lattice
$a(G)\geq b(G)$
. Inequality (2) allows us to translate any upper bound on the percolation threshold of a lattice
![]() $G$
into a lower bound on the exponential growth rate of lattice animals
$G$
into a lower bound on the exponential growth rate of lattice animals
![]() $a(G)$
and vice versa. We exploit this in both directions. We improve on the best known asymptotic lower and upper bounds on
$a(G)$
and vice versa. We exploit this in both directions. We improve on the best known asymptotic lower and upper bounds on
![]() $a({\mathbb{Z}}^d)$
as
$a({\mathbb{Z}}^d)$
as
![]() $d\to \infty$
, answering a question of Barequet, Barequet and Rote [Reference Barequet, Barequet and Rote4]. We use percolation as a tool to obtain the latter, and conversely, we use the former to obtain lower bounds on
$d\to \infty$
, answering a question of Barequet, Barequet and Rote [Reference Barequet, Barequet and Rote4]. We use percolation as a tool to obtain the latter, and conversely, we use the former to obtain lower bounds on
![]() $p_c({\mathbb{Z}}^d)$
.
$p_c({\mathbb{Z}}^d)$
.
1.3. Lattice animals vs. interfaces
Inequality (2) remains true if we replace
![]() $b(G)$
by the exponential growth rate
$b(G)$
by the exponential growth rate
![]() $a(G)$
of lattice animals, and all ingredients for its proof are available in [Reference Hammond19]. In this paper, we provide a unified, and simpler, approach to proving such inequalities. Our definition of interface is parametrised by a choice of a basis
$a(G)$
of lattice animals, and all ingredients for its proof are available in [Reference Hammond19]. In this paper, we provide a unified, and simpler, approach to proving such inequalities. Our definition of interface is parametrised by a choice of a basis
![]() $\mathcal{P}$
of the cycle space
$\mathcal{P}$
of the cycle space
![]() ${\mathcal{C}}(G)$
of the lattice
${\mathcal{C}}(G)$
of the lattice
![]() $G$
. We elaborate on this notion in Sections 3 and 4. By varying the choice of
$G$
. We elaborate on this notion in Sections 3 and 4. By varying the choice of
![]() $\mathcal{P}$
, we obtain a spectrum of notions of
$\mathcal{P}$
, we obtain a spectrum of notions of
![]() $\mathcal{P}$
interface, which are always relevant to percolation: we showed in [Reference Georgakopoulos and Panagiotis17, Theorem 10.4] (restated as Theorem 3.7 below) that every finite connected subgraph of
$\mathcal{P}$
interface, which are always relevant to percolation: we showed in [Reference Georgakopoulos and Panagiotis17, Theorem 10.4] (restated as Theorem 3.7 below) that every finite connected subgraph of
![]() $G$
, for example a percolation cluster, contains a unique
$G$
, for example a percolation cluster, contains a unique
![]() $\mathcal{P}$
interface. One extreme of this spectrum is where
$\mathcal{P}$
interface. One extreme of this spectrum is where
![]() $\mathcal{P}$
is just the set of all cycles of
$\mathcal{P}$
is just the set of all cycles of
![]() $G$
, in which case the
$G$
, in which case the
![]() $\mathcal{P}$
interfaces coincide with the lattice animals. The other extreme is where
$\mathcal{P}$
interfaces coincide with the lattice animals. The other extreme is where
![]() $\mathcal{P}$
is a minimal basis, in which case the
$\mathcal{P}$
is a minimal basis, in which case the
![]() $\mathcal{P}$
interface of a percolation cluster is a thin layer incident with its boundary to infinity. For example, when
$\mathcal{P}$
interface of a percolation cluster is a thin layer incident with its boundary to infinity. For example, when
![]() $G$
is the square lattice, and
$G$
is the square lattice, and
![]() $\mathcal{P}$
comprises its squares of length
$\mathcal{P}$
comprises its squares of length
![]() $4$
, then the (unique)
$4$
, then the (unique)
![]() $\mathcal{P}$
interface contained in a finite connected subgraph
$\mathcal{P}$
interface contained in a finite connected subgraph
![]() $C$
consists of the vertices and edges at the boundary of the unbounded face
$C$
consists of the vertices and edges at the boundary of the unbounded face
![]() $F$
of
$F$
of
![]() $C$
in the plane. Here, we think of
$C$
in the plane. Here, we think of
![]() $C$
as a plane graph inheriting its embedding into
$C$
as a plane graph inheriting its embedding into
![]() ${\mathbb{R}}^2$
from
${\mathbb{R}}^2$
from
![]() $G$
, and the unbounded face of
$G$
, and the unbounded face of
![]() $C$
is its unique face of infinite diameter. Some examples of such interfaces are depicted in Figure 2. The main message of this paper is that this second extreme of
$C$
is its unique face of infinite diameter. Some examples of such interfaces are depicted in Figure 2. The main message of this paper is that this second extreme of
![]() $\mathcal{P}$
interfaces provides finer information about percolation. In particular, we will prove (Theorem 10.1) that for every basis
$\mathcal{P}$
interfaces provides finer information about percolation. In particular, we will prove (Theorem 10.1) that for every basis
![]() $\mathcal{P}$
comprising cycles of bounded length the following holds:
$\mathcal{P}$
comprising cycles of bounded length the following holds:
Theorem 1.1.
![]() $b(G)\lt a(G)$
holds for every
$b(G)\lt a(G)$
holds for every
![]() $G\in \mathcal{S}$
.
$G\in \mathcal{S}$
.
We remark that using this theorem and inequality (2), we obtain the strict inequality
1.4. Growth rates parametrised by ‘volume-to-surface ratio’
Before stating our other results, we need to introduce more terminology. Recall that when considering counts
![]() $A_{n,m}$
of lattice animals, it was important to parametrise them both by their size
$A_{n,m}$
of lattice animals, it was important to parametrise them both by their size
![]() $n$
and their boundary size
$n$
and their boundary size
![]() $m$
. Alternatively, instead of
$m$
. Alternatively, instead of
![]() $m$
we could use the ‘volume-to-surface ratio’
$m$
we could use the ‘volume-to-surface ratio’
![]() $n/m$
. Similarly, to establish (2), we consider the exponential growth rate
$n/m$
. Similarly, to establish (2), we consider the exponential growth rate
![]() $b_r=b_r(G)$
of the number of interfaces of
$b_r=b_r(G)$
of the number of interfaces of
![]() $G$
with size
$G$
with size
![]() $n$
and volume-to-surface ratio approximating
$n$
and volume-to-surface ratio approximating
![]() $r$
, as a function of
$r$
, as a function of
![]() $r\in{\mathbb{R}}_+$
. By ‘volume’ here we mean the number of edges contained in an interface
$r\in{\mathbb{R}}_+$
. By ‘volume’ here we mean the number of edges contained in an interface
![]() $P$
, and by ‘surface’ we mean the cardinality of a set
$P$
, and by ‘surface’ we mean the cardinality of a set
![]() $\partial P$
of edges that are incident with
$\partial P$
of edges that are incident with
![]() $P$
and are ‘accessible’ from infinity. (See Definition 3.6 for details.) In the example of Figure 2, the edges in
$P$
and are ‘accessible’ from infinity. (See Definition 3.6 for details.) In the example of Figure 2, the edges in
![]() $\partial P$
are depicted by dashed lines.
$\partial P$
are depicted by dashed lines.
We consider this function
![]() $b_r(G)$
to be of independent interest; in fact, most of this paper revolves around it. In particular, we prove that
$b_r(G)$
to be of independent interest; in fact, most of this paper revolves around it. In particular, we prove that
![]() $b_r(G)$
is always continuous (Theorem 6.4) and log-concave (Theorem 6.3).
$b_r(G)$
is always continuous (Theorem 6.4) and log-concave (Theorem 6.3).
One of the best known results of percolation theory is the exponential decay, as
![]() $n\to \infty$
, of the cluster size distribution
$n\to \infty$
, of the cluster size distribution
![]() ${\mathbb{P}}_p(|C_o|= n)$
for
${\mathbb{P}}_p(|C_o|= n)$
for
![]() $p$
in the subcritical interval
$p$
in the subcritical interval
![]() $[0,p_c)$
[Reference Aizenman and Barsky1]. In the supercritical case
$[0,p_c)$
[Reference Aizenman and Barsky1]. In the supercritical case
![]() $p\in (p_c,1)$
, this exponential decay holds for some, but not all, lattices and values of
$p\in (p_c,1)$
, this exponential decay holds for some, but not all, lattices and values of
![]() $p$
[Reference Aizenman, Delyon and Souillard2, Reference Hermon and Hutchcroft24].
$p$
[Reference Aizenman, Delyon and Souillard2, Reference Hermon and Hutchcroft24].
Letting
![]() $S_o \subseteq C_o$
denote the interface of
$S_o \subseteq C_o$
denote the interface of
![]() $C_o$
, we can analogously ask for which
$C_o$
, we can analogously ask for which
![]() $p\in (0,1)$
we have exponential decay of the probability
$p\in (0,1)$
we have exponential decay of the probability
![]() ${\mathbb{P}}_p(|S_o|= n)$
. We prove that this is uniquely determined by the value
${\mathbb{P}}_p(|S_o|= n)$
. We prove that this is uniquely determined by the value
![]() $b_{r(p)}$
, where
$b_{r(p)}$
, where
![]() $r(p)\,:\!=\frac{1-p}{p}$
is a bijection between the parameter spaces of edge density
$r(p)\,:\!=\frac{1-p}{p}$
is a bijection between the parameter spaces of edge density
![]() $p$
and volume-to-surface ratio
$p$
and volume-to-surface ratio
![]() $r$
(we consider bond percolation in this section, but we will also discuss site percolation later on). More concretely, we observe that, firstly,
$r$
(we consider bond percolation in this section, but we will also discuss site percolation later on). More concretely, we observe that, firstly,
![]() $b_{r(p)}(G) \leq f(r(p))$
holds for every lattice
$b_{r(p)}(G) \leq f(r(p))$
holds for every lattice
![]() $G$
and every
$G$
and every
![]() $p\in (0,1)$
, where
$p\in (0,1)$
, where
![]() $f(r)$
is the aforementioned universal function (Proposition 4.4), and secondly,
$f(r)$
is the aforementioned universal function (Proposition 4.4), and secondly,
![]() ${\mathbb{P}}_p(|S_o|= n)$
decays exponentially in
${\mathbb{P}}_p(|S_o|= n)$
decays exponentially in
![]() $n$
for exactly those values of
$n$
for exactly those values of
![]() $p$
for which this inequality is strict:
$p$
for which this inequality is strict:
Theorem 1.2.
Let
![]() $G\in \mathcal{S}$
. Then for every
$G\in \mathcal{S}$
. Then for every
![]() $p\in (0,1)$
, the interface size distribution
$p\in (0,1)$
, the interface size distribution
![]() ${\mathbb{P}}_p( |S_o|=n )$
fails to decay exponentially in
${\mathbb{P}}_p( |S_o|=n )$
fails to decay exponentially in
![]() $n$
if and only if
$n$
if and only if
![]() $$b_{r(p)}(G)= f(r(p)).$$
$$b_{r(p)}(G)= f(r(p)).$$
Incidentally, we prove in the Appendix that the rate of the exponential decay of
![]() ${\mathbb{P}}_p(|C_o|= n)$
, defined as
${\mathbb{P}}_p(|C_o|= n)$
, defined as
![]() $c(p)\,:\!= \lim _n \left ({\mathbb{P}}_p(|C_o|= n)\right )^{1/n}$
(see [Reference Bandyopadhyay, Steif and Timár3, Reference Grimmett18] for a proof that the limit exists for every
$c(p)\,:\!= \lim _n \left ({\mathbb{P}}_p(|C_o|= n)\right )^{1/n}$
(see [Reference Bandyopadhyay, Steif and Timár3, Reference Grimmett18] for a proof that the limit exists for every
![]() $p\in (0,1)$
), is a continuous function of
$p\in (0,1)$
), is a continuous function of
![]() $p$
(Theorem 12.1). Our proof boils down to elementary calculations not involving our notion of interface. Another contribution of this paper is the subexponential decay at
$p$
(Theorem 12.1). Our proof boils down to elementary calculations not involving our notion of interface. Another contribution of this paper is the subexponential decay at
![]() $1-p_c$
for triangulated lattices in
$1-p_c$
for triangulated lattices in
![]() ${\mathbb{R}}^d$
(Corollary 5.7).
${\mathbb{R}}^d$
(Corollary 5.7).
We expect our results to hold for more general vertex-transitive 1-ended graphs, but decided to restrict our attention to
![]() $\mathcal{S}$
to avoid technicalities that would add little to the understanding of the matter.
$\mathcal{S}$
to avoid technicalities that would add little to the understanding of the matter.
It is interesting that Theorem 1.2 holds for every choice of basis
![]() $\mathcal{P}$
with respect to which our interfaces are defined. In particular, since lattice animals are a special case of
$\mathcal{P}$
with respect to which our interfaces are defined. In particular, since lattice animals are a special case of
![]() $\mathcal{P}$
interfaces as mentioned above, we can replace the interface size distribution
$\mathcal{P}$
interfaces as mentioned above, we can replace the interface size distribution
![]() ${\mathbb{P}}_p( |S_o|=n )$
by the cluster size distribution
${\mathbb{P}}_p( |S_o|=n )$
by the cluster size distribution
![]() ${\mathbb{P}}_p( |C_o|=n )$
and
${\mathbb{P}}_p( |C_o|=n )$
and
![]() $b_{r(p)}(G)$
by its analogue
$b_{r(p)}(G)$
by its analogue
![]() $a_{r(p)}(G)$
counting lattice animals. This form of Theorem 1.2 was proved by Hammond [Reference Hammond19] building on a result of Delyon [Reference Delyon11].
$a_{r(p)}(G)$
counting lattice animals. This form of Theorem 1.2 was proved by Hammond [Reference Hammond19] building on a result of Delyon [Reference Delyon11].
Our proof of Theorem 1.2 is based on a large deviation principle for interfaces (Lemma 4.7) that may be of independent interest. Roughly speaking, the latter result says that for any
![]() $p\in (0,1)$
, most occurring interfaces have a volume-to-surface ratio close to the value
$p\in (0,1)$
, most occurring interfaces have a volume-to-surface ratio close to the value
![]() $r(p)$
.
$r(p)$
.
We mentioned above that the most refined extreme of such results is obtained when
![]() $\mathcal{P}$
is a minimal basis. This is even more so for ‘triangulated’ lattices, that is lattices having a basis
$\mathcal{P}$
is a minimal basis. This is even more so for ‘triangulated’ lattices, that is lattices having a basis
![]() $\mathcal{P}$
consisting of triangles. For such a lattice, we show that the following holds.
$\mathcal{P}$
consisting of triangles. For such a lattice, we show that the following holds.
Theorem 1.3.
Let
![]() $G\in \mathcal{S}$
, and suppose that the cycle space of
$G\in \mathcal{S}$
, and suppose that the cycle space of
![]() $G$
is generated by its triangles. Then,
$G$
is generated by its triangles. Then,
![]() $b_r= (b_{1/r})^r$
for every
$b_r= (b_{1/r})^r$
for every
![]() $r\gt 0$
.
$r\gt 0$
.
In other words, the values of
![]() $b_r$
for
$b_r$
for
![]() $r\lt 1$
determine those for
$r\lt 1$
determine those for
![]() $r\gt 1$
(Theorems 5.1 and 5.2). This is the technically most involved result of this paper. It shows that considering interfaces rather than lattice animals yields a differently behaved function
$r\gt 1$
(Theorems 5.1 and 5.2). This is the technically most involved result of this paper. It shows that considering interfaces rather than lattice animals yields a differently behaved function
![]() $b_r$
, namely one with no intersection with
$b_r$
, namely one with no intersection with
![]() $f(r)$
not only for
$f(r)$
not only for
![]() $r\gt r(p_c)$
but also for
$r\gt r(p_c)$
but also for
![]() $r\lt 1/r(p_c)$
. Most of our knowledge about
$r\lt 1/r(p_c)$
. Most of our knowledge about
![]() $b_r$
is summarised in Figure 1.
$b_r$
is summarised in Figure 1.

Figure 1. An approximate, conjectural, visualisation of
![]() $b_r(G)$
when
$b_r(G)$
when
![]() $G$
is a lattice in
$G$
is a lattice in
![]() ${\mathbb{R}}^d, d\geq 3$
. The graph of
${\mathbb{R}}^d, d\geq 3$
. The graph of
![]() $b_r(G)$
(depicted in bold ink) lies below the graph of
$b_r(G)$
(depicted in bold ink) lies below the graph of
![]() $f(r)\,:\!= \frac{(1+r)^{1+r}}{r^r}$
(depicted in blue, if colour is shown). The fact that
$f(r)\,:\!= \frac{(1+r)^{1+r}}{r^r}$
(depicted in blue, if colour is shown). The fact that
![]() $f(r)$
plots almost like a straight line can be seen by rewriting it as
$f(r)$
plots almost like a straight line can be seen by rewriting it as
![]() $(1+r)(1+1/r)^r$
. The fact that
$(1+r)(1+1/r)^r$
. The fact that
![]() $b_r= f(r)$
for
$b_r= f(r)$
for
![]() $r$
in the interval
$r$
in the interval
![]() $(r(1-p_c), r(p_c)]$
, where
$(r(1-p_c), r(p_c)]$
, where
![]() $r(p)\,:\!= \frac{1-p}{p}$
, follows by combining a theorem of Kesten & Zhang [Reference Kesten and Zhang29], saying that exponential decay of
$r(p)\,:\!= \frac{1-p}{p}$
, follows by combining a theorem of Kesten & Zhang [Reference Kesten and Zhang29], saying that exponential decay of
![]() ${\mathbb{P}}_p(|S_o|= n)$
fails in that interval, with our Theorem 1.2. That
${\mathbb{P}}_p(|S_o|= n)$
fails in that interval, with our Theorem 1.2. That
![]() $b_r\lt f(r)$
for
$b_r\lt f(r)$
for
![]() $r\gt r(p_c)$
follows from the well-known exponential decay of
$r\gt r(p_c)$
follows from the well-known exponential decay of
![]() ${\mathbb{P}}_p(|C_o|= n)$
for
${\mathbb{P}}_p(|C_o|= n)$
for
![]() $p\lt p_c$
[Reference Aizenman and Barsky1]. We also know that
$p\lt p_c$
[Reference Aizenman and Barsky1]. We also know that
![]() $b_r$
is continuous and log-concave. The continuity of
$b_r$
is continuous and log-concave. The continuity of
![]() $b_r$
, combined with Theorem 1.2 again, implies failure of the exponential decay at
$b_r$
, combined with Theorem 1.2 again, implies failure of the exponential decay at
![]() $p=1-p_c$
(Corollary 5.7), which was not obtained in [Reference Kesten and Zhang29]. If the cycle space of
$p=1-p_c$
(Corollary 5.7), which was not obtained in [Reference Kesten and Zhang29]. If the cycle space of
![]() $G$
is generated by its triangles, then Theorem 1.3 determines the subcritical branch
$G$
is generated by its triangles, then Theorem 1.3 determines the subcritical branch
![]() $r\gt r(p_c)$
given the branch
$r\gt r(p_c)$
given the branch
![]() $r\lt r(1-p_c)$
and vice versa. For the planar triangular lattice, the picture degenerates as
$r\lt r(1-p_c)$
and vice versa. For the planar triangular lattice, the picture degenerates as
![]() $p_c=1-p_c=1/2$
, and so
$p_c=1-p_c=1/2$
, and so
![]() $b_r= f(r)$
for
$b_r= f(r)$
for
![]() $r=r(1/2)=1$
only. Note that
$r=r(1/2)=1$
only. Note that
![]() $b_r(G)$
is an invariant of
$b_r(G)$
is an invariant of
![]() $G$
defined without reference to any random experiment. The connection to percolation is established by Theorem 1.2 via the above transformation
$G$
defined without reference to any random experiment. The connection to percolation is established by Theorem 1.2 via the above transformation
![]() $r(p)$
. Since
$r(p)$
. Since
![]() $r(p)$
is monotone decreasing in
$r(p)$
is monotone decreasing in
![]() $p$
, the right-hand side of Figure 1 corresponds to the subcritical percolation regime, and the left-hand side to the supercritical. Using the transformation
$p$
, the right-hand side of Figure 1 corresponds to the subcritical percolation regime, and the left-hand side to the supercritical. Using the transformation
![]() $r\to \frac 1{r}$
(from volume-to-surface into surface-to-volume ratio), we could reverse the picture to have the ‘subcritical’ interval on the left. For ‘triangulated’ lattices, the picture would look exactly the same due to Theorem 1.3, only the positions of
$r\to \frac 1{r}$
(from volume-to-surface into surface-to-volume ratio), we could reverse the picture to have the ‘subcritical’ interval on the left. For ‘triangulated’ lattices, the picture would look exactly the same due to Theorem 1.3, only the positions of
![]() $r(p_c)$
and
$r(p_c)$
and
![]() $r(1-p_c)$
would be interchanged.
$r(1-p_c)$
would be interchanged.
Amusingly, our universal function
![]() $f(r)$
also satisfies the equation of Theorem 1.3, that is
$f(r)$
also satisfies the equation of Theorem 1.3, that is
![]() $f(r)= f(1/r)^r$
.
$f(r)= f(1/r)^r$
.
1.5. Bounds on lattice animals
Obtaining reasonable bounds on the count
![]() $a_n({\mathbb{Z}}^d)$
of
$a_n({\mathbb{Z}}^d)$
of
![]() $d$
-dimensional lattice animals of size
$d$
-dimensional lattice animals of size
![]() $n$
containing the origin is very difficult to come by even in 2 dimensions, and so the mainstream focuses on their exponential growth rates
$n$
containing the origin is very difficult to come by even in 2 dimensions, and so the mainstream focuses on their exponential growth rates
![]() $a({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{a_n({\mathbb{Z}}^d)}^{1/n}$
. These have important interactions with statistical mechanics models such as percolation theory, the present paper being an instance of this interaction. Some precise asymptotic expansions for
$a({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{a_n({\mathbb{Z}}^d)}^{1/n}$
. These have important interactions with statistical mechanics models such as percolation theory, the present paper being an instance of this interaction. Some precise asymptotic expansions for
![]() $a({\mathbb{Z}}^d)$
and its site counterpart
$a({\mathbb{Z}}^d)$
and its site counterpart
![]() $\dot{a}({\mathbb{Z}}^d)$
were reported in the physics literature [Reference Gaunt and Peard15, Reference Harris22, Reference Peard and Gaunt38] but without any rigorous bounds on the error terms. Miranda and Slade [Reference Miranda and Slade36, Reference Miranda and Slade37] determined the first three terms of the
$\dot{a}({\mathbb{Z}}^d)$
were reported in the physics literature [Reference Gaunt and Peard15, Reference Harris22, Reference Peard and Gaunt38] but without any rigorous bounds on the error terms. Miranda and Slade [Reference Miranda and Slade36, Reference Miranda and Slade37] determined the first three terms of the
![]() $1/d$
expansion of
$1/d$
expansion of
![]() $a({\mathbb{Z}}^d)$
rigorously.
$a({\mathbb{Z}}^d)$
rigorously.
Much less is known about its site variant
![]() $\dot{a}({\mathbb{Z}}^d)$
. Barequet, Barequet, and Rote in [Reference Barequet, Barequet and Rote4] proved that
$\dot{a}({\mathbb{Z}}^d)$
. Barequet, Barequet, and Rote in [Reference Barequet, Barequet and Rote4] proved that
![]() $\dot{a}({\mathbb{Z}}^d)=2de-o(d)$
. Peard and Gaunt had previously made involved, but nonrigorous, calculations that yield
$\dot{a}({\mathbb{Z}}^d)=2de-o(d)$
. Peard and Gaunt had previously made involved, but nonrigorous, calculations that yield
![]() $\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
[Reference Peard and Gaunt38, (2.22)] and [Reference Barequet, Barequet and Rote4] expressed the belief that this is correct. Our first result is that this prediction is indeed right as a lower bound (Theorem 7.5). We deduce this from a recent bound of Heydenreich and Matzke [Reference Heydenreich and Matzke25] on the site percolation threshold
$\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
[Reference Peard and Gaunt38, (2.22)] and [Reference Barequet, Barequet and Rote4] expressed the belief that this is correct. Our first result is that this prediction is indeed right as a lower bound (Theorem 7.5). We deduce this from a recent bound of Heydenreich and Matzke [Reference Heydenreich and Matzke25] on the site percolation threshold
![]() ${\dot{p}_c}({\mathbb{Z}}^d)$
, obtained using an involved technique called lace expansion. (The dot in
${\dot{p}_c}({\mathbb{Z}}^d)$
, obtained using an involved technique called lace expansion. (The dot in
![]() ${\dot{p}_c}({\mathbb{Z}}^d),\dot{a}({\mathbb{Z}}^d)$
etc. means that we are considering site percolation, or lattice site animals; most of our results have a bond and a site version.) To do so, we exploit the aforementioned formula (2).
${\dot{p}_c}({\mathbb{Z}}^d),\dot{a}({\mathbb{Z}}^d)$
etc. means that we are considering site percolation, or lattice site animals; most of our results have a bond and a site version.) To do so, we exploit the aforementioned formula (2).
The aforementioned upper bound of [Reference Barequet, Barequet and Rote4] was improved to
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
in simultaneous work by Barequet and Shalah [Reference Barequet and Shalah6]. We improve this further asymptotically to
$\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
in simultaneous work by Barequet and Shalah [Reference Barequet and Shalah6]. We improve this further asymptotically to
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-5e/2+O(1/\log\! (d))$
(Theorem 8.1). For this, we use direct combinatorial arguments that do not involve percolation. We can then plug this bound into (the site version of) (2) to obtain the lower bound
$\dot{a}({\mathbb{Z}}^d)\leq 2de-5e/2+O(1/\log\! (d))$
(Theorem 8.1). For this, we use direct combinatorial arguments that do not involve percolation. We can then plug this bound into (the site version of) (2) to obtain the lower bound
![]() ${\dot{p}_c}({\mathbb{Z}}^d)\geq \frac{1}{2d}+\frac{2}{(2d)^2}-O(1/d^2\log\! (d))$
(Theorem 8.4). This bound was improved by Heydenreich and Matzke [Reference Heydenreich and Matzke25] shortly after the first draft of our work appeared, see (17).
${\dot{p}_c}({\mathbb{Z}}^d)\geq \frac{1}{2d}+\frac{2}{(2d)^2}-O(1/d^2\log\! (d))$
(Theorem 8.4). This bound was improved by Heydenreich and Matzke [Reference Heydenreich and Matzke25] shortly after the first draft of our work appeared, see (17).
In this paper, we used percolation as a tool to bound
![]() $\dot{a}({\mathbb{Z}}^d)$
from above. Another method was introduced by Eden [Reference Eden13] using more direct counting arguments. This method was enhanced by Klarner and Rivest [Reference Klarner and Rivest31] in the case of
$\dot{a}({\mathbb{Z}}^d)$
from above. Another method was introduced by Eden [Reference Eden13] using more direct counting arguments. This method was enhanced by Klarner and Rivest [Reference Klarner and Rivest31] in the case of
![]() ${\mathbb{Z}}^2$
, who obtained that
${\mathbb{Z}}^2$
, who obtained that
![]() $\dot{a}({\mathbb{Z}}^2)\leq 4.6496$
, and more recently by Barequet and Shalah [Reference Barequet and Shalah6], who obtained the asymptotic inequality
$\dot{a}({\mathbb{Z}}^2)\leq 4.6496$
, and more recently by Barequet and Shalah [Reference Barequet and Shalah6], who obtained the asymptotic inequality
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
. In dimension
$\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
. In dimension
![]() $3$
, the same paper proves
$3$
, the same paper proves
![]() $\dot{a}({\mathbb{Z}}^3)\lt 9.3835$
. Plugging this into (2), we deduce
$\dot{a}({\mathbb{Z}}^3)\lt 9.3835$
. Plugging this into (2), we deduce
![]() $\dot{p}_c({\mathbb{Z}}^3)\gt 0.2522$
, which is the best rigorous lower bound known.
$\dot{p}_c({\mathbb{Z}}^3)\gt 0.2522$
, which is the best rigorous lower bound known.
1.6. Improvements for non-amenable graphs
A well-known theorem of Benjamini & Schramm [Reference Benjamini and Schramm8] states that
![]() $p_c(G)\leq \frac{1}{h(G)+1}$
, where
$p_c(G)\leq \frac{1}{h(G)+1}$
, where
![]() $h(G)$
denotes the Cheeger constant. We show that this inequality is in fact strict, that is
$h(G)$
denotes the Cheeger constant. We show that this inequality is in fact strict, that is
when
![]() $G$
is
$G$
is
![]() $1$
-ended, has bounded degrees, and its cycle space admits a basis consisting of cycles of bounded length (Theorem 10.2). Moreover, in Section 9 we define a variant
$1$
-ended, has bounded degrees, and its cycle space admits a basis consisting of cycles of bounded length (Theorem 10.2). Moreover, in Section 9 we define a variant
![]() $I(G)$
of the Cheeger constant by considering interfaces rather than arbitrary finite subgraphs of
$I(G)$
of the Cheeger constant by considering interfaces rather than arbitrary finite subgraphs of
![]() $G$
. We obtain the strengthening
$G$
. We obtain the strengthening
![]() $p_c(G)\leq \frac{1}{I(G)+1}$
of the aforementioned theorem (Theorem 9.2), which again has a site and a bond version. We remark that, unlike
$p_c(G)\leq \frac{1}{I(G)+1}$
of the aforementioned theorem (Theorem 9.2), which again has a site and a bond version. We remark that, unlike
![]() $h(G)$
, our
$h(G)$
, our
![]() $I(G)$
can be positive even for amenable graphs. When
$I(G)$
can be positive even for amenable graphs. When
![]() $G$
is the planar square lattice for example, it is not hard to see that
$G$
is the planar square lattice for example, it is not hard to see that
![]() $I(G)=1/2$
in the bond case, which yields the Peierls bound
$I(G)=1/2$
in the bond case, which yields the Peierls bound
![]() $p_c\leq 2/3$
. Moreover, one can have
$p_c\leq 2/3$
. Moreover, one can have
![]() $I(G)\gt h(G)$
even in the non-amenable case: this turns out to be the case for regular triangulations and quadrangulations of the hyperbolic plane as proved in a companion paper [Reference Haslegrave and Panagiotis23].
$I(G)\gt h(G)$
even in the non-amenable case: this turns out to be the case for regular triangulations and quadrangulations of the hyperbolic plane as proved in a companion paper [Reference Haslegrave and Panagiotis23].
1.7. Structure
This paper is structured as follows. Section 2 contains some standard definitions and results that will be used in several places later on. Section 3 recalls the notion of an interface and some of its properties obtained in [Reference Georgakopoulos and Panagiotis17]. Section 4 introduces
![]() $b_r$
and presents the proof of the inequality
$b_r$
and presents the proof of the inequality
![]() $b_r\leq f(r)$
and Theorem 1.2. Sections 5 and 6 contain a proof of Theorem 1.3 and the fact that
$b_r\leq f(r)$
and Theorem 1.2. Sections 5 and 6 contain a proof of Theorem 1.3 and the fact that
![]() $b_r$
is well-behaved, namely continuous and log-concave. In Sections 7 and 8, we obtain the bounds on lattice animals and the lower bound on
$b_r$
is well-behaved, namely continuous and log-concave. In Sections 7 and 8, we obtain the bounds on lattice animals and the lower bound on
![]() $\dot{p}_c({\mathbb{Z}}^3)$
. The last two sections are devoted to the new bounds on
$\dot{p}_c({\mathbb{Z}}^3)$
. The last two sections are devoted to the new bounds on
![]() $p_c$
for non-amenable graphs and to the proof of Theorem 1.1. The Appendix contains a proof that the rate of the exponential decay of the cluster size distribution of Bernoulli percolation is a continuous function of
$p_c$
for non-amenable graphs and to the proof of Theorem 1.1. The Appendix contains a proof that the rate of the exponential decay of the cluster size distribution of Bernoulli percolation is a continuous function of
![]() $p\in (0,1)$
. An analogous result is proved for interfaces as well.
$p\in (0,1)$
. An analogous result is proved for interfaces as well.
2. Definitions and preliminaries
2.1. Percolation
We recall some standard definitions of percolation theory. For more details, the reader can consult, for example, [Reference Bollobás and Riordan9, Reference Grimmett18, Reference Lyons and Peres33].
Let
![]() $G = (V,E)$
be a countably infinite graph, and let
$G = (V,E)$
be a countably infinite graph, and let
![]() $\Omega \,:\!= \{0,1\}^E$
be the set of percolation configurations on
$\Omega \,:\!= \{0,1\}^E$
be the set of percolation configurations on
![]() $G$
. We say that an edge
$G$
. We say that an edge
![]() $e$
is vacant (respectively, occupied) in a percolation configuration
$e$
is vacant (respectively, occupied) in a percolation configuration
![]() $\omega \in \Omega$
, if
$\omega \in \Omega$
, if
![]() $\omega (e)=0$
(resp.
$\omega (e)=0$
(resp.
![]() $\omega (e)=1$
).
$\omega (e)=1$
).
By Bernoulli bond percolation on
![]() $G$
with parameter
$G$
with parameter
![]() $p\in [0,1]$
, we mean the random subgraph of
$p\in [0,1]$
, we mean the random subgraph of
![]() $G$
obtained by keeping each edge with probability
$G$
obtained by keeping each edge with probability
![]() $p$
and deleting it with probability
$p$
and deleting it with probability
![]() $1-p$
, with these decisions being independent of each other.
$1-p$
, with these decisions being independent of each other.
The percolation threshold
![]() $p_c(G)$
is defined by
$p_c(G)$
is defined by
where the cluster
![]() $C_o$
of
$C_o$
of
![]() $o\in V$
is the component of
$o\in V$
is the component of
![]() $o$
in the subgraph of
$o$
in the subgraph of
![]() $G$
spanned by the occupied edges. It is easy to see that
$G$
spanned by the occupied edges. It is easy to see that
![]() $p_c(G)$
does not depend on the choice of
$p_c(G)$
does not depend on the choice of
![]() $o$
.
$o$
.
To define site percolation, we repeat the same definitions, except that we now let
![]() $\Omega \,:\!= \{0,1\}^V$
, and let
$\Omega \,:\!= \{0,1\}^V$
, and let
![]() $C_o$
be the component of
$C_o$
be the component of
![]() $o$
in the subgraph of
$o$
in the subgraph of
![]() $G$
induced by the occupied vertices. The percolation threshold for site percolation is denoted
$G$
induced by the occupied vertices. The percolation threshold for site percolation is denoted
![]() $\dot{p}_c$
.
$\dot{p}_c$
.
In this paper, the graphs
![]() $G$
we consider are all countably infinite, connected, and every vertex has finite degree. Some of our results will need assumptions on
$G$
we consider are all countably infinite, connected, and every vertex has finite degree. Some of our results will need assumptions on
![]() $G$
like (quasi-)vertex transitivity or planarity, but these will be explicitly stated as needed.
$G$
like (quasi-)vertex transitivity or planarity, but these will be explicitly stated as needed.
2.2. Graph-theoretic definitions
Let
![]() $G = (V,E)$
be a graph. An induced subgraph
$G = (V,E)$
be a graph. An induced subgraph
![]() $H$
of
$H$
of
![]() $G$
is a subgraph that contains all edges
$G$
is a subgraph that contains all edges
![]() $xy$
of
$xy$
of
![]() $G$
with
$G$
with
![]() $x,y\in V(H)$
. Note that
$x,y\in V(H)$
. Note that
![]() $H$
is uniquely determined by its vertex set. The subgraph of
$H$
is uniquely determined by its vertex set. The subgraph of
![]() $G$
spanned by a vertex set
$G$
spanned by a vertex set
![]() $S\subseteq V(G)$
is the induced subgraph of
$S\subseteq V(G)$
is the induced subgraph of
![]() $G$
with vertex set
$G$
with vertex set
![]() $S$
. The vertex set of a graph
$S$
. The vertex set of a graph
![]() $G$
will be denoted by
$G$
will be denoted by
![]() $V(G)$
, and its edge set by
$V(G)$
, and its edge set by
![]() $E(G)$
. The degree of a vertex
$E(G)$
. The degree of a vertex
![]() $v\in V(G)$
is the number of edges of
$v\in V(G)$
is the number of edges of
![]() $G$
containing
$G$
containing
![]() $v$
.
$v$
.
The edge space of a graph
![]() $G$
is the direct sum
$G$
is the direct sum
![]() ${\mathcal E}(G)\,:\!= \bigoplus _{e\in E(G)}{\mathbb{Z}}_2$
, where
${\mathcal E}(G)\,:\!= \bigoplus _{e\in E(G)}{\mathbb{Z}}_2$
, where
![]() ${\mathbb{Z}}_2=\{0,1\}$
is the field of two elements, which we consider as a vector space over
${\mathbb{Z}}_2=\{0,1\}$
is the field of two elements, which we consider as a vector space over
![]() ${\mathbb{Z}}_2$
. The cycle space
${\mathbb{Z}}_2$
. The cycle space
![]() ${\mathcal{C}}(G)$
of
${\mathcal{C}}(G)$
of
![]() $G$
is the subspace of
$G$
is the subspace of
![]() ${\mathcal E}(G)$
spanned by the circuits of cycles, where a circuit is an element
${\mathcal E}(G)$
spanned by the circuits of cycles, where a circuit is an element
![]() $C\in{\mathcal E}(G)$
whose non-zero coordinates
$C\in{\mathcal E}(G)$
whose non-zero coordinates
![]() $\{e\in E(G) \mid C_e=1\}$
coincide with the edge set of a cycle of
$\{e\in E(G) \mid C_e=1\}$
coincide with the edge set of a cycle of
![]() $G$
. By a cycle, we mean a connected subgraph
$G$
. By a cycle, we mean a connected subgraph
![]() $C$
every vertex of which lies in exactly two edges of
$C$
every vertex of which lies in exactly two edges of
![]() $C$
.
$C$
.
Given a subgraph
![]() $S$
of
$S$
of
![]() ${\mathbb{Z}}^d$
, the edge boundary
${\mathbb{Z}}^d$
, the edge boundary
![]() $\partial _E S$
of
$\partial _E S$
of
![]() $S$
is the set of edges of
$S$
is the set of edges of
![]() ${\mathbb{Z}}^d$
that have at least one end vertex in
${\mathbb{Z}}^d$
that have at least one end vertex in
![]() $S$
but are not contained in
$S$
but are not contained in
![]() $S$
. The vertex boundary
$S$
. The vertex boundary
![]() $\partial _V S$
of
$\partial _V S$
of
![]() $S$
is the set of vertices of
$S$
is the set of vertices of
![]() ${\mathbb{Z}}^d$
that have a neighbour in
${\mathbb{Z}}^d$
that have a neighbour in
![]() $S$
but are not contained in
$S$
but are not contained in
![]() $S$
.
$S$
.
A planar graph
![]() $G$
is a graph that can be embedded in the plane
$G$
is a graph that can be embedded in the plane
![]() ${\mathbb{R}}^2$
, that is it can be drawn in such a way that no edges cross each other. Such an embedding is called a planar embedding of the graph. A plane graph is a (planar) graph endowed with a fixed planar embedding. Alternatively, we can think of a plane graph as a subspace of
${\mathbb{R}}^2$
, that is it can be drawn in such a way that no edges cross each other. Such an embedding is called a planar embedding of the graph. A plane graph is a (planar) graph endowed with a fixed planar embedding. Alternatively, we can think of a plane graph as a subspace of
![]() ${\mathbb{R}}^2$
homeomorphic to an 1-complex.
${\mathbb{R}}^2$
homeomorphic to an 1-complex.
A plane graph
![]() $G$
divides the plane into regions called faces, that is each face is a connected component of
$G$
divides the plane into regions called faces, that is each face is a connected component of
![]() ${\mathbb{R}}^2\setminus G$
. Using the faces of a plane graph
${\mathbb{R}}^2\setminus G$
. Using the faces of a plane graph
![]() $G$
, we define its dual graph
$G$
, we define its dual graph
![]() $G^*$
as follows. The vertices of
$G^*$
as follows. The vertices of
![]() $G^*$
are the faces of
$G^*$
are the faces of
![]() $G$
, and we connect two vertices of
$G$
, and we connect two vertices of
![]() $G^*$
with an edge whenever the corresponding faces of
$G^*$
with an edge whenever the corresponding faces of
![]() $G$
share an edge. Thus, there is a bijection
$G$
share an edge. Thus, there is a bijection
![]() $e\mapsto e^*$
from
$e\mapsto e^*$
from
![]() $E(G)$
to
$E(G)$
to
![]() $E(G^*)$
.
$E(G^*)$
.
Given a subgraph
![]() $H$
of a graph
$H$
of a graph
![]() $G$
and a positive integer
$G$
and a positive integer
![]() $k$
, we define the k-neighbourhood of
$k$
, we define the k-neighbourhood of
![]() $H$
to be the set of vertices at distance at most
$H$
to be the set of vertices at distance at most
![]() $k$
from
$k$
from
![]() $H$
.
$H$
.
2.3. Partitions
A partition of a positive integer
![]() $n$
is a multiset
$n$
is a multiset
![]() $\{m_1,m_2,\ldots,m_k\}$
of positive integers such that
$\{m_1,m_2,\ldots,m_k\}$
of positive integers such that
![]() $m_1+m_2+\ldots +m_k=n$
. Let
$m_1+m_2+\ldots +m_k=n$
. Let
![]() $p(n)$
denote the number of partitions of
$p(n)$
denote the number of partitions of
![]() $n$
. An asymptotic expression for
$n$
. An asymptotic expression for
![]() $p(n)$
was given by Hardy & Ramanujan in their famous paper [Reference Hardy and Ramanujan21]. An elementary proof of this formula up to a multiplicative constant was given by Erdős [Reference Erdos14]. As customary, we use
$p(n)$
was given by Hardy & Ramanujan in their famous paper [Reference Hardy and Ramanujan21]. An elementary proof of this formula up to a multiplicative constant was given by Erdős [Reference Erdos14]. As customary, we use
![]() $A\sim B$
to denote the relation
$A\sim B$
to denote the relation
![]() $A/B\rightarrow 1$
as
$A/B\rightarrow 1$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Theorem 2.1 (Hardy-Ramanujan formula). The number
![]() $p(n)$
of partitions of
$p(n)$
of partitions of
![]() $n$
satisfies
$n$
satisfies
 \begin{equation*}p(n)\sim \dfrac {1}{4n\sqrt {3}}\exp \left (\pi \sqrt {\dfrac {2n}{3}}\right ).\end{equation*}
\begin{equation*}p(n)\sim \dfrac {1}{4n\sqrt {3}}\exp \left (\pi \sqrt {\dfrac {2n}{3}}\right ).\end{equation*}
(We do not need the full strength of Theorem 2.1 in this paper; any subexponential upper bound on
![]() $p(n)$
would suffice, and such bounds are much easier to obtain. See for example [Reference Georgakopoulos and Panagiotis17, Lemma 3.4].)
$p(n)$
would suffice, and such bounds are much easier to obtain. See for example [Reference Georgakopoulos and Panagiotis17, Lemma 3.4].)
2.4. Doubly periodic planar lattices
In this subsection, we will consider graphs that embed in
![]() $\mathbb{R}^2$
, in a ‘nice’ way.
$\mathbb{R}^2$
, in a ‘nice’ way.
Definition 2.2. A doubly periodic planar lattice is a locally finite, connected, plane graph
![]() $G$
without accumulation points of vertices, such that for some linearly independent vectors
$G$
without accumulation points of vertices, such that for some linearly independent vectors
![]() $v_1,v_2\in{\mathbb{R}}^2$
, translation by each
$v_1,v_2\in{\mathbb{R}}^2$
, translation by each
![]() $v_i$
preserves
$v_i$
preserves
![]() $G$
.
$G$
.
Notice that any action as in Definition 2.2 has finitely many orbits of vertices.
Definition 2.3.
Given a finite subgraph
![]() $H$
of an infinite graph
$H$
of an infinite graph
![]() $G$
, the minimal edge cut
$G$
, the minimal edge cut
![]() $\partial ^E H$
of
$\partial ^E H$
of
![]() $H$
is defined to be the minimal set of edges lying in
$H$
is defined to be the minimal set of edges lying in
![]() $E(G)\setminus E(H)$
with at least one end vertex in
$E(G)\setminus E(H)$
with at least one end vertex in
![]() $H$
, the removal of which disconnects
$H$
, the removal of which disconnects
![]() $H$
from infinity. The minimal vertex cut
$H$
from infinity. The minimal vertex cut
![]() $\partial ^V H$
of
$\partial ^V H$
of
![]() $H$
is the minimal set of vertices in
$H$
is the minimal set of vertices in
![]() $V(G)\setminus V(H)$
that are incident to
$V(G)\setminus V(H)$
that are incident to
![]() $H$
, the removal of which disconnects
$H$
, the removal of which disconnects
![]() $H$
from infinity.
$H$
from infinity.
To see that the minimal sets in the above definition are unique, note that
![]() $\partial ^E H$
and
$\partial ^E H$
and
![]() $\partial ^V H$
can be defined equivalently as the sets of edges/vertices that are incident to
$\partial ^V H$
can be defined equivalently as the sets of edges/vertices that are incident to
![]() $H$
and connected to infinity in the complement of
$H$
and connected to infinity in the complement of
![]() $\partial _E H$
and
$\partial _E H$
and
![]() $\partial _V H$
, respectively.
$\partial _V H$
, respectively.
It is not hard to see that doubly periodic planar lattices are quasi-isometric to
![]() ${\mathbb{R}}^2$
, inheriting some of its geometric properties. More precisely, any doubly periodic planar lattice
${\mathbb{R}}^2$
, inheriting some of its geometric properties. More precisely, any doubly periodic planar lattice
![]() $G$
$G$
-
P1 has quadratic growth, that is there are constants
 $c_1=c_1(G),c_2=c_2(G)\gt 0$
such thatfor every
$c_1=c_1(G),c_2=c_2(G)\gt 0$
such thatfor every \begin{equation*}c_1 n^2\leq |B(u,n)|\leq c_2 n^2\end{equation*}
\begin{equation*}c_1 n^2\leq |B(u,n)|\leq c_2 n^2\end{equation*}
 $u\in V(G)$
and every positive integer
$u\in V(G)$
and every positive integer
 $n$
, where
$n$
, where
 $B(u,n)$
denotes the ball of radius
$B(u,n)$
denotes the ball of radius
 $n$
around
$n$
around
 $u$
in either graph-theoretic distance or Euclidean distance,
$u$
in either graph-theoretic distance or Euclidean distance,
-
P2 satisfies a
 $2$
-dimensional isoperimetric inequality, that is there is a constant
$2$
-dimensional isoperimetric inequality, that is there is a constant
 $c=c(G)\gt 0$
such that for any finite subgraph
$c=c(G)\gt 0$
such that for any finite subgraph
 $H\subset G$
,
$H\subset G$
, \begin{equation*}|\partial ^V H|\geq c \sqrt {|H|}.\end{equation*}
\begin{equation*}|\partial ^V H|\geq c \sqrt {|H|}.\end{equation*}
It will be useful to define a more general type of isoperimetric inequality.
-
P3 Given a positive number
 $d$
(not necessarily an integer), we say that a graph
$d$
(not necessarily an integer), we say that a graph
 $G$
satisfies a
$G$
satisfies a
 $d$
-dimensional isoperimetric inequality if there is a constant
$d$
-dimensional isoperimetric inequality if there is a constant
 $c\gt 0$
such that for any finite subgraph
$c\gt 0$
such that for any finite subgraph
 $H\subset G$
,
$H\subset G$
, \begin{equation*}|\partial ^V H|\geq c |H|^{\frac {d-1}{d}}.\end{equation*}
\begin{equation*}|\partial ^V H|\geq c |H|^{\frac {d-1}{d}}.\end{equation*}
Any doubly periodic planar lattice
![]() $G$
is easily seen to satisfy the following properties as well:
$G$
is easily seen to satisfy the following properties as well:
-
P4 For some
 $o\in V(G)$
, there is a
$o\in V(G)$
, there is a
 $2$
-way infinite path
$2$
-way infinite path
 $X=(\ldots,x_{-1},x_0=o,x_1,\ldots )$
containing
$X=(\ldots,x_{-1},x_0=o,x_1,\ldots )$
containing
 $o$
and a constant
$o$
and a constant
 $\ell \gt 0$
, such that
$\ell \gt 0$
, such that
 $d_X(x_i,x_j)\leq \ell d_G(x_i,x_j)$
for every
$d_X(x_i,x_j)\leq \ell d_G(x_i,x_j)$
for every
 $i,j\in \mathbb{Z}$
, where
$i,j\in \mathbb{Z}$
, where
 $d_X$
and
$d_X$
and
 $d_G$
denote distance in
$d_G$
denote distance in
 $X$
and
$X$
and
 $G$
, respectively. Moreover, it is not too hard to see that we can choose
$G$
, respectively. Moreover, it is not too hard to see that we can choose
 $X$
to be periodic, that is to satisfy
$X$
to be periodic, that is to satisfy
 $X+ t v_1= X$
for some
$X+ t v_1= X$
for some
 $t\in{\mathbb N}$
. Any such path is called a quasi-geodesic.
$t\in{\mathbb N}$
. Any such path is called a quasi-geodesic. -
P5 The cycle space of
 $G$
is generated by cycles of bounded length.
$G$
is generated by cycles of bounded length.Indeed, a natural choice for a basis of the cycle space of
 $G$
is the set of cycles which bound a face of
$G$
is the set of cycles which bound a face of
 $G$
, which all have length bounded by a uniform constant by periodicity.
$G$
, which all have length bounded by a uniform constant by periodicity. -
P6
 $G$
is
$G$
is
 $1$
-ended, that is for every finite subgraph
$1$
-ended, that is for every finite subgraph
 $H$
of
$H$
of
 $G$
, the graph
$G$
, the graph
 $G\setminus H$
has a unique infinite component.
$G\setminus H$
has a unique infinite component.
3. Interfaces
In this section, we recall the notions of (bond-)interfaces and site interfaces introduced in [Reference Georgakopoulos and Panagiotis17]. In most cases, we will work with the following families of graphs:
-
(a) doubly periodic planar lattices,
-
(b) the standard cubic lattice
 ${\mathbb{Z}}^d$
,
${\mathbb{Z}}^d$
,
 $d\geq 2$
,
$d\geq 2$
, -
(c)
 $\mathbb{T}^d$
, the graph obtained by adding to
$\mathbb{T}^d$
, the graph obtained by adding to
 ${\mathbb{Z}}^d$
,
${\mathbb{Z}}^d$
,
 $d\geq 2$
the ‘monotone’ diagonal edges, that is the edges of the form
$d\geq 2$
the ‘monotone’ diagonal edges, that is the edges of the form
 $xy$
where
$xy$
where
 $y_i-x_i=1$
for exactly two coordinates
$y_i-x_i=1$
for exactly two coordinates
 $i\leq d$
, and
$i\leq d$
, and
 $y_i=x_i$
for all other coordinates (
$y_i=x_i$
for all other coordinates (
 $\mathbb{T}^2$
is isomorphic to the triangular lattice).
$\mathbb{T}^2$
is isomorphic to the triangular lattice).
Definition 3.1.
We define
![]() $\mathcal{S}$
to be the set of all
$\mathcal{S}$
to be the set of all
![]() $2$
-connected doubly periodic planar lattices, and the lattices
$2$
-connected doubly periodic planar lattices, and the lattices
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
for
$\mathbb{T}^d$
for
![]() $d\geq 2$
.
$d\geq 2$
.
Remark 3.2. The
![]() $2$
-connectedness restriction is helpful because it implies that every vertex is contained in a cycle of the graph. This is only a minor restriction, because any cut vertices separate finite components by 1-endedness, and those components can be removed to obtain a
$2$
-connectedness restriction is helpful because it implies that every vertex is contained in a cycle of the graph. This is only a minor restriction, because any cut vertices separate finite components by 1-endedness, and those components can be removed to obtain a
![]() $2$
-connected doubly periodic planar lattice on which percolation behaves in the same way as in the initial graph, for example it has the same
$2$
-connected doubly periodic planar lattice on which percolation behaves in the same way as in the initial graph, for example it has the same
![]() $p_c$
, for a fixed
$p_c$
, for a fixed
![]() $p\in (0,1)$
either
$p\in (0,1)$
either
![]() ${\mathbb{P}}_p(|S_o|=n)$
decays exponentially for both graphs or for none of them, etc.
${\mathbb{P}}_p(|S_o|=n)$
decays exponentially for both graphs or for none of them, etc.
Our motivation for considering
![]() $\mathbb{T}^d$
is that
$\mathbb{T}^d$
is that
![]() ${\mathbb{Z}}^d$
fails to satisfy Theorem 1.3, our deepest result, while
${\mathbb{Z}}^d$
fails to satisfy Theorem 1.3, our deepest result, while
![]() $\mathbb{T}^d$
is a ‘minimal’ supergraph of
$\mathbb{T}^d$
is a ‘minimal’ supergraph of
![]() ${\mathbb{Z}}^d$
that satisfies it. The reason for this is that
${\mathbb{Z}}^d$
that satisfies it. The reason for this is that
![]() $\mathbb{T}^d$
satisfies the assumption that the cycle space is generated by triangles, while
$\mathbb{T}^d$
satisfies the assumption that the cycle space is generated by triangles, while
![]() ${\mathbb{Z}}^d$
does not. The same applies to variants of
${\mathbb{Z}}^d$
does not. The same applies to variants of
![]() $\mathbb{T}^d$
obtained by adding more ‘diagonal’ edges, but we will refrain from discussing those variants.
$\mathbb{T}^d$
obtained by adding more ‘diagonal’ edges, but we will refrain from discussing those variants.
For each
![]() $G\in \mathcal{S}$
, we will fix a basis
$G\in \mathcal{S}$
, we will fix a basis
![]() $\mathcal{P}=\mathcal{P}(G)$
of the cycle space
$\mathcal{P}=\mathcal{P}(G)$
of the cycle space
![]() ${\mathcal{C}}(G)$
(defined in Section 2.2). If
${\mathcal{C}}(G)$
(defined in Section 2.2). If
![]() $G$
is a doubly periodic planar lattice,
$G$
is a doubly periodic planar lattice,
![]() $\mathcal{P}$
consists of the cycles bounding the faces of
$\mathcal{P}$
consists of the cycles bounding the faces of
![]() $G$
. For
$G$
. For
![]() $G={\mathbb{Z}}^d$
, we can use the squares of length
$G={\mathbb{Z}}^d$
, we can use the squares of length
![]() $4$
as our basis
$4$
as our basis
![]() $\mathcal{P}$
, and for
$\mathcal{P}$
, and for
![]() $G=\mathbb{T}^d$
, we can use the triangles obtained from the squares of length
$G=\mathbb{T}^d$
, we can use the triangles obtained from the squares of length
![]() $4$
once we add the ‘monotone’ diagonal edges. Our definition of the interface of
$4$
once we add the ‘monotone’ diagonal edges. Our definition of the interface of
![]() $G$
depends on the choice of
$G$
depends on the choice of
![]() $\mathcal{P}(G)$
, and so in [Reference Georgakopoulos and Panagiotis17], we used the notation ‘
$\mathcal{P}(G)$
, and so in [Reference Georgakopoulos and Panagiotis17], we used the notation ‘
![]() $\mathcal{P}$
interface’ to emphasise the dependence. Since in this paper we are fixing
$\mathcal{P}$
interface’ to emphasise the dependence. Since in this paper we are fixing
![]() $\mathcal{P}(G)$
for each
$\mathcal{P}(G)$
for each
![]() $G\in \mathcal{S}$
, we will simplify our notation and just talk about interfaces.
$G\in \mathcal{S}$
, we will simplify our notation and just talk about interfaces.
Let us start by defining interfaces for doubly periodic planar lattices.
Definition 3.3.
Let
![]() $G$
be a doubly periodic planar lattice and
$G$
be a doubly periodic planar lattice and
![]() $o$
a vertex of
$o$
a vertex of
![]() $G$
. A subgraph
$G$
. A subgraph
![]() $P$
of
$P$
of
![]() $G$
is called a (bond-)interface (of
$G$
is called a (bond-)interface (of
![]() $o$
) if there is a finite connected subgraph
$o$
) if there is a finite connected subgraph
![]() $H$
of
$H$
of
![]() $G$
containing
$G$
containing
![]() $o$
such that
$o$
such that
![]() $P$
consists of the vertices and edges incident with the unbounded face of
$P$
consists of the vertices and edges incident with the unbounded face of
![]() $H$
. The boundary
$H$
. The boundary
![]() $\partial P$
of
$\partial P$
of
![]() $P$
is the set of edges of
$P$
is the set of edges of
![]() $G$
that are incident with
$G$
that are incident with
![]() $P$
and lie in the unbounded face of
$P$
and lie in the unbounded face of
![]() $H$
. We say that an interface occurs in a bond percolation configuration
$H$
. We say that an interface occurs in a bond percolation configuration
![]() $\omega$
if all edges in
$\omega$
if all edges in
![]() $P$
are occupied and all edges in
$P$
are occupied and all edges in
![]() $\partial P$
are vacant.
$\partial P$
are vacant.
As remarked in [Reference Georgakopoulos and Panagiotis17, Proposition 10.7] interfaces are connected graphs and satisfy the following property.
Lemma 3.4.
For any doubly periodic planar lattice
![]() $G$
, if two interfaces of
$G$
, if two interfaces of
![]() $G$
occur in the same percolation configuration
$G$
occur in the same percolation configuration
![]() $\omega$
and share a vertex then they coincide.
$\omega$
and share a vertex then they coincide.
With some thought, this notion can be generalised to higher dimensions in such a way that a unique interface is associated with any cluster. The reader may already have their own favourite definition of interface for
![]() $G={\mathbb{Z}}^d$
or
$G={\mathbb{Z}}^d$
or
![]() $G=\mathbb{T}^d$
, and as long as that definition satisfies Theorem 3.7 below, it will coincide with ours. For the remaining readers, we offer the following abstract definition. For (site percolation on)
$G=\mathbb{T}^d$
, and as long as that definition satisfies Theorem 3.7 below, it will coincide with ours. For the remaining readers, we offer the following abstract definition. For (site percolation on)
![]() $G=\mathbb{T}^d$
, we offer a simpler alternative definition implicit in Proposition 3.9.
$G=\mathbb{T}^d$
, we offer a simpler alternative definition implicit in Proposition 3.9.
In [Reference Georgakopoulos and Panagiotis17], we were able to define interfaces in much greater generality than that of graphs in
![]() $\mathcal{S}$
, namely in every
$\mathcal{S}$
, namely in every
![]() $1$
-ended,
$1$
-ended,
![]() $2$
-connected graph
$2$
-connected graph
![]() $G$
. These interfaces have the important property that in any percolation configuration, occurring interfaces are in 1-to-1 correspondence with percolation clusters (Theorem 3.7 below). A priori it is not clear that such a general and well-behaved definition of interface is possible. To come up with it, we have tried to capture the important features of interfaces in Definition 3.3 without reference to the embedding of
$G$
. These interfaces have the important property that in any percolation configuration, occurring interfaces are in 1-to-1 correspondence with percolation clusters (Theorem 3.7 below). A priori it is not clear that such a general and well-behaved definition of interface is possible. To come up with it, we have tried to capture the important features of interfaces in Definition 3.3 without reference to the embedding of
![]() $G$
. For this, we noticed that fixing an embedding of a graph into
$G$
. For this, we noticed that fixing an embedding of a graph into
![]() ${\mathbb{R}}^2$
is tantamount to fixing the cycles that bound faces. Thus to generalise Definition 3.3 to an arbitrary graph, we need a notion of ‘face boundaries’. The role of this notion is played in our definition by a choice of a generating set of a cycle space
${\mathbb{R}}^2$
is tantamount to fixing the cycles that bound faces. Thus to generalise Definition 3.3 to an arbitrary graph, we need a notion of ‘face boundaries’. The role of this notion is played in our definition by a choice of a generating set of a cycle space
![]() ${\mathcal{C}}(G)$
of
${\mathcal{C}}(G)$
of
![]() $G$
. (For an 1-ended 2-connected plane graph, the face boundaries form a basis of the cycle space.)
$G$
. (For an 1-ended 2-connected plane graph, the face boundaries form a basis of the cycle space.)
We proceed with our formal definition of interfaces. From now on, we will be assuming that
Every edge
![]() $e=vw\in E(G)$
has two directions
$e=vw\in E(G)$
has two directions
![]() $\vec{vw},\overleftarrow{wv}$
, which are the two directed sets comprising
$\vec{vw},\overleftarrow{wv}$
, which are the two directed sets comprising
![]() $v,w$
. We let
$v,w$
. We let
![]() $\overleftrightarrow{E(G)}$
denote the set of all directions of edges in
$\overleftrightarrow{E(G)}$
denote the set of all directions of edges in
![]() $E(G)$
. The head
$E(G)$
. The head
![]() $head(\vec{vw})$
of
$head(\vec{vw})$
of
![]() $\vec{vw}$
is
$\vec{vw}$
is
![]() $w$
. Given
$w$
. Given
![]() $F\subset E(G)$
and a subgraph
$F\subset E(G)$
and a subgraph
![]() $D$
of
$D$
of
![]() $G$
, let
$G$
, let
![]() ${\vec{F^{D}}}\,:\!= \{\vec{vz} \mid vz\in F, z\in V(D) \}$
be the set of directions of the elements of
${\vec{F^{D}}}\,:\!= \{\vec{vz} \mid vz\in F, z\in V(D) \}$
be the set of directions of the elements of
![]() $F$
towards
$F$
towards
![]() $D$
.
$D$
.
Let
![]() $\mathcal{P}$
denote a basis of
$\mathcal{P}$
denote a basis of
![]() ${\mathcal{C}}(G)$
(which in the particular case of
${\mathcal{C}}(G)$
(which in the particular case of
![]() $\mathcal{S}$
we fixed at the beginning of this section). A
$\mathcal{S}$
we fixed at the beginning of this section). A
![]() $\mathcal{P}$
-path connecting two directed edges
$\mathcal{P}$
-path connecting two directed edges
![]() $\vec{vw}, \overleftarrow{yx} \in \overleftrightarrow{E(G)}$
is a path
$\vec{vw}, \overleftarrow{yx} \in \overleftrightarrow{E(G)}$
is a path
![]() $P$
of
$P$
of
![]() $G$
such that the extension
$G$
such that the extension
![]() $vw P yx$
is a subpath of an element of
$vw P yx$
is a subpath of an element of
![]() $\mathcal{P}$
. Here, the notation
$\mathcal{P}$
. Here, the notation
![]() $vw P yx$
denotes the path with edge set
$vw P yx$
denotes the path with edge set
![]() $E(P) \cup \{vw, yx\}$
, with the understanding that the end vertices of
$E(P) \cup \{vw, yx\}$
, with the understanding that the end vertices of
![]() $P$
are
$P$
are
![]() $w,y$
. Note that
$w,y$
. Note that
![]() $P$
is not endowed with any notion of direction, but the directions of the edges
$P$
is not endowed with any notion of direction, but the directions of the edges
![]() $\vec{vw}, \overleftarrow{yx}$
it connects do matter. We allow
$\vec{vw}, \overleftarrow{yx}$
it connects do matter. We allow
![]() $P$
to consist of a single vertex
$P$
to consist of a single vertex
![]() $w=y$
.
$w=y$
.
We will say that
![]() $P$
connects an undirected edge
$P$
connects an undirected edge
![]() $e\in E(G)$
to
$e\in E(G)$
to
![]() $\vec{f}\in \overleftrightarrow{E(G)}$
(respectively, to a set
$\vec{f}\in \overleftrightarrow{E(G)}$
(respectively, to a set
![]() $J\subset \overleftrightarrow{E(G)}$
), if
$J\subset \overleftrightarrow{E(G)}$
), if
![]() $P$
is a
$P$
is a
![]() $\mathcal{P}$
-path connecting one of the two directions of
$\mathcal{P}$
-path connecting one of the two directions of
![]() $e$
to
$e$
to
![]() $\vec{f}$
(resp. to some element of
$\vec{f}$
(resp. to some element of
![]() $J$
).
$J$
).
Definition 3.5.
We say that a set
![]() ${J}\subset \overleftrightarrow{E(G)}$
is
${J}\subset \overleftrightarrow{E(G)}$
is
![]() $F$
-connected for some
$F$
-connected for some
![]() $F\subset E(G)$
, if for every proper bipartition
$F\subset E(G)$
, if for every proper bipartition
![]() $ ({J_1},{J_2})$
of
$ ({J_1},{J_2})$
of
![]() $J$
, there is a
$J$
, there is a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G$
that avoids
$G$
that avoids
![]() $F$
and connects an element of
$F$
and connects an element of
![]() $J_1$
to an element of
$J_1$
to an element of
![]() $J_2$
.
$J_2$
.
We are now ready to give the formal definition of the central notion of the paper.
Definition 3.6.
A (bond-)interface of
![]() $G$
is a pair
$G$
is a pair
![]() $(P,\partial P)$
of sets of edges of
$(P,\partial P)$
of sets of edges of
![]() $G$
with the following properties
$G$
with the following properties
-
(i)
 $\partial P$
separates
$\partial P$
separates
 $o$
from infinity;
$o$
from infinity;
-
(ii) Exactly one finite component of
 $G\setminus \partial P$
, denoted by
$G\setminus \partial P$
, denoted by
 $D$
, contains a vertex of each edge in
$D$
, contains a vertex of each edge in
 $\partial P$
;
$\partial P$
; -
(iii)
 $\vec{\partial P^{D}}$
is
$\vec{\partial P^{D}}$
is
 $\partial P$
-connected; and
$\partial P$
-connected; and
-
(iv)
 $P = \big\{e \in E(D) \mid \text{ there is\ a $\mathcal{P}$-path in $G\setminus \partial P$ connecting $e$ to ${\vec{\partial P^{D}}}$ }\big\}$
.
$P = \big\{e \in E(D) \mid \text{ there is\ a $\mathcal{P}$-path in $G\setminus \partial P$ connecting $e$ to ${\vec{\partial P^{D}}}$ }\big\}$
.
Recall that we are thinking of
![]() $\mathcal{P}$
as a generalisation of the face boundaries of a planar graph. Notice that for
$\mathcal{P}$
as a generalisation of the face boundaries of a planar graph. Notice that for
![]() $P$
as in Definition 3.3, the faces outside
$P$
as in Definition 3.3, the faces outside
![]() $P$
connect the edges in
$P$
connect the edges in
![]() $\partial P$
. Condition (iii) is the analogue of this observation.
$\partial P$
. Condition (iii) is the analogue of this observation.
We say that an interface
![]() $(P,\partial P)$
occurs in a bond percolation configuration
$(P,\partial P)$
occurs in a bond percolation configuration
![]() $\omega$
if the edges of
$\omega$
if the edges of
![]() $P$
are occupied, and the edges of
$P$
are occupied, and the edges of
![]() $\partial P$
are vacant. Moreover, we say that
$\partial P$
are vacant. Moreover, we say that
![]() $(P,\partial P)$
meets a cluster
$(P,\partial P)$
meets a cluster
![]() $C$
of
$C$
of
![]() $\omega$
, if either
$\omega$
, if either
![]() $P\cap E(C)\neq \emptyset$
, or
$P\cap E(C)\neq \emptyset$
, or
![]() $P = E(C) =\emptyset$
and
$P = E(C) =\emptyset$
and
![]() $\partial P=\partial C$
, where
$\partial P=\partial C$
, where
![]() $\partial C$
is the set edges in
$\partial C$
is the set edges in
![]() $E(G)\setminus E(C)$
with at least one end vertex in
$E(G)\setminus E(C)$
with at least one end vertex in
![]() $C$
(in which case
$C$
(in which case
![]() $C$
consists of
$C$
consists of
![]() $o$
only).
$o$
only).
Example 1: Let
![]() $G$
be a 2-connected doubly periodic planar lattice, and let
$G$
be a 2-connected doubly periodic planar lattice, and let
![]() $\mathcal{P}$
consist of the cycles bounding a face of
$\mathcal{P}$
consist of the cycles bounding a face of
![]() $G$
. Then, Definitions 3.3 and 3.6 agree. It would be a good exercise for the reader to check this in specific cases: draw a portion of your favourite lattice, and a random finite connected subgraph
$G$
. Then, Definitions 3.3 and 3.6 agree. It would be a good exercise for the reader to check this in specific cases: draw a portion of your favourite lattice, and a random finite connected subgraph
![]() $H$
. Guess what the interface
$H$
. Guess what the interface
![]() $P$
of
$P$
of
![]() $H$
should be based on Definition 3.3. Then, check that the pair
$H$
should be based on Definition 3.3. Then, check that the pair
![]() $(P,\partial P)$
as in Definition 3.3 satisfies the conditions of Definition 3.6.
$(P,\partial P)$
as in Definition 3.3 satisfies the conditions of Definition 3.6.
Example 2: Let
![]() $G$
be any 1-ended 2-connected graph, and choose
$G$
be any 1-ended 2-connected graph, and choose
![]() $\mathcal{P}$
to be the set of all cycles of
$\mathcal{P}$
to be the set of all cycles of
![]() $G$
. Then for every finite
$G$
. Then for every finite
![]() $P\subset E(G)$
spanning a connected subgraph of
$P\subset E(G)$
spanning a connected subgraph of
![]() $G$
, the pair
$G$
, the pair
![]() $(P,\partial P)$
is an interface, where
$(P,\partial P)$
is an interface, where
![]() $\partial P$
is the set of edges of
$\partial P$
is the set of edges of
![]() $G$
incident with
$G$
incident with
![]() $P$
. To see this, use the fact that every pair of edges of
$P$
. To see this, use the fact that every pair of edges of
![]() $\partial P$
lies in a common cycle
$\partial P$
lies in a common cycle
![]() $C$
by 2-connectedness. Notice the rigidity: there is no
$C$
by 2-connectedness. Notice the rigidity: there is no
![]() $Q\neq \partial P\subset E(G)$
such that
$Q\neq \partial P\subset E(G)$
such that
![]() $(P,Q)$
is an interface.
$(P,Q)$
is an interface.
Example 3: We can ‘interpolate’ between examples 1 and 2 by fixing
![]() $G$
and
$G$
and
![]() $H$
, and varying
$H$
, and varying
![]() $\mathcal{P}$
. For example, let
$\mathcal{P}$
. For example, let
![]() $H$
be the ball of radius
$H$
be the ball of radius
![]() $N\in{\mathbb N}$
around
$N\in{\mathbb N}$
around
![]() $o$
, and let
$o$
, and let
![]() $\mathcal{P} =\mathcal{P}_r$
consist of all cycles of
$\mathcal{P} =\mathcal{P}_r$
consist of all cycles of
![]() $G$
of length at most
$G$
of length at most
![]() $r$
. Then, there is a unique interface
$r$
. Then, there is a unique interface
![]() $(P,\partial P)$
such that
$(P,\partial P)$
such that
![]() $\partial P=\partial H$
, and
$\partial P=\partial H$
, and
![]() $P$
becomes thicker as
$P$
becomes thicker as
![]() $r$
grows.
$r$
grows.
The following result shows that in any percolation configuration, occurring interfaces are in 1-to-1 correspondence with percolation clusters.
Theorem 3.7 ([Reference Georgakopoulos and Panagiotis17, Theorem 10.4]). Let
![]() $G$
be an 1-ended, 2-connected graph, and
$G$
be an 1-ended, 2-connected graph, and
![]() $\omega$
a (site) percolation configuration. For every finite (site) percolation cluster
$\omega$
a (site) percolation configuration. For every finite (site) percolation cluster
![]() $C$
of
$C$
of
![]() $\omega$
such that
$\omega$
such that
![]() $\partial _E C$
separates
$\partial _E C$
separates
![]() $o$
from infinity, there is a unique (site)interface
$o$
from infinity, there is a unique (site)interface
![]() $(P,\partial P)$
that meets
$(P,\partial P)$
that meets
![]() $C$
and occurs. Moreover, we have
$C$
and occurs. Moreover, we have
![]() $P\subset E(C)$
and
$P\subset E(C)$
and
![]() $\partial P\subset \partial C$
.
$\partial P\subset \partial C$
.
Conversely, every occurring (site)interface meets a unique percolation cluster
![]() $C$
, and
$C$
, and
![]() $\partial C$
separates
$\partial C$
separates
![]() $o$
from infinity (in particular,
$o$
from infinity (in particular,
![]() $C$
is finite).
$C$
is finite).
The above result allows us to define the interface of a finite cluster
![]() $C$
of a percolation configuration
$C$
of a percolation configuration
![]() $\omega$
as the unique occurring interface that meets
$\omega$
as the unique occurring interface that meets
![]() $C$
. (There can be clusters
$C$
. (There can be clusters
![]() $C$
that separate
$C$
that separate
![]() $o$
from infinity and do not contain
$o$
from infinity and do not contain
![]() $o$
; for example, if
$o$
; for example, if
![]() $G$
is planar,
$G$
is planar,
![]() $C$
could be a cycle around
$C$
could be a cycle around
![]() $o$
.)
$o$
.)
(Bond-)interfaces are specifically designed to study bond percolation on
![]() $G$
. There is a natural analogue for site percolation. For an interface
$G$
. There is a natural analogue for site percolation. For an interface
![]() $(Q,\partial Q)$
of
$(Q,\partial Q)$
of
![]() $G$
, we let
$G$
, we let
![]() $V(Q)$
denote the set of vertices incident with an edge in
$V(Q)$
denote the set of vertices incident with an edge in
![]() $Q$
, and we let
$Q$
, and we let
![]() $V(\partial Q)$
denote the set of vertices in
$V(\partial Q)$
denote the set of vertices in
![]() $V\setminus V(Q)$
which are incident with an edge in
$V\setminus V(Q)$
which are incident with an edge in
![]() $\partial Q$
. We say that a pair
$\partial Q$
. We say that a pair
![]() $(P,\partial P)$
of vertex sets is a site interface, if
$(P,\partial P)$
of vertex sets is a site interface, if
![]() $P=V(Q)$
and
$P=V(Q)$
and
![]() $\partial P=V(\partial Q)$
for a bond-interface
$\partial P=V(\partial Q)$
for a bond-interface
![]() $(Q,\partial Q)$
with the property that no edge in
$(Q,\partial Q)$
with the property that no edge in
![]() $\partial Q$
has both its end vertices in
$\partial Q$
has both its end vertices in
![]() $V(Q)$
. We emphasise that a site interface is a pair of vertex sets, while a bond interface is a pair of edge sets. This is a crucial difference for results such as Theorem 3.7.
$V(Q)$
. We emphasise that a site interface is a pair of vertex sets, while a bond interface is a pair of edge sets. This is a crucial difference for results such as Theorem 3.7.
We say that a site interface
![]() $(P,\partial P)$
occurs in a site percolation configuration
$(P,\partial P)$
occurs in a site percolation configuration
![]() $\omega$
if the vertices of
$\omega$
if the vertices of
![]() $P$
are occupied, and the vertices of
$P$
are occupied, and the vertices of
![]() $\partial P$
are vacant. We define the site interface of a cluster
$\partial P$
are vacant. We define the site interface of a cluster
![]() $C$
of a site percolation configuration
$C$
of a site percolation configuration
![]() $\omega$
as the occurring site interface that has at least one common vertex with
$\omega$
as the occurring site interface that has at least one common vertex with
![]() $C$
. The fact that there exists a unique such site interface follows from Theorem 3.7.
$C$
. The fact that there exists a unique such site interface follows from Theorem 3.7.
Remark 3.8. Let
![]() $G$
be a graph whose cycle space admits a basis consisting of cycles of length bounded by some constant
$G$
be a graph whose cycle space admits a basis consisting of cycles of length bounded by some constant
![]() $t\gt 0$
. Then for every interface
$t\gt 0$
. Then for every interface
![]() $(P,\partial P)$
of
$(P,\partial P)$
of
![]() $G$
, and any pair of edges in
$G$
, and any pair of edges in
![]() $\partial P$
, there is a path contained in the
$\partial P$
, there is a path contained in the
![]() $t/2$
-neighbourhood of
$t/2$
-neighbourhood of
![]() $\partial P$
connecting the pair (see [Reference Georgakopoulos and Panagiotis17, p. 47]).
$\partial P$
connecting the pair (see [Reference Georgakopoulos and Panagiotis17, p. 47]).
We define a (site)multi-interface to be a finite collection of (site)interfaces
![]() $(P_1,\partial P_1),\ldots,(P_n,\partial P_n)$
such that the sets
$(P_1,\partial P_1),\ldots,(P_n,\partial P_n)$
such that the sets
![]() $P_i$
are pairwise disjoint. An example is shown in Figure 2.
$P_i$
are pairwise disjoint. An example is shown in Figure 2.

Figure 2. An example of a multi-interface
![]() $M$
, comprising two nested interfaces
$M$
, comprising two nested interfaces
![]() $P_1,P_2$
. We depict
$P_1,P_2$
. We depict
![]() $M$
with bold lines, and
$M$
with bold lines, and
![]() $\partial M\,:\!= \partial P_1 \cup \partial P_2$
with dashed lines (green, if colour is shown). The edges not participating in
$\partial M\,:\!= \partial P_1 \cup \partial P_2$
with dashed lines (green, if colour is shown). The edges not participating in
![]() $M$
are depicted in plain lines (blue, if colour is shown).
$M$
are depicted in plain lines (blue, if colour is shown).
In the case where
site interfaces admit an equivalent definition that is more standard and easier to work with:
Proposition 3.9.
Let
![]() $G\in \mathcal{S}$
be a graph satisfying (4), and let
$G\in \mathcal{S}$
be a graph satisfying (4), and let
![]() $D$
be a finite induced subgraph of
$D$
be a finite induced subgraph of
![]() $G$
containing
$G$
containing
![]() $o$
. Let
$o$
. Let
![]() $\overline{D}$
be the union of
$\overline{D}$
be the union of
![]() $D$
with the finite connected components of
$D$
with the finite connected components of
![]() $G\setminus D$
. Define
$G\setminus D$
. Define
![]() $P$
to be the set of vertices of
$P$
to be the set of vertices of
![]() $\overline{D}$
which have a neighbour not in
$\overline{D}$
which have a neighbour not in
![]() $\overline{D}$
, and let
$\overline{D}$
, and let
![]() $\partial P$
be the set of vertices of
$\partial P$
be the set of vertices of
![]() $G\setminus \overline{D}$
that have a neighbour in
$G\setminus \overline{D}$
that have a neighbour in
![]() $\overline{D}$
. Then,
$\overline{D}$
. Then,
![]() $(P,\partial P)$
is the site interface of
$(P,\partial P)$
is the site interface of
![]() $D$
. Moreover, any site interface can be obtained in this way.
$D$
. Moreover, any site interface can be obtained in this way.
Proof. Let us start from the last statement which is easier to prove. By definition, for every site interface
![]() $(P,\partial P)$
,
$(P,\partial P)$
,
![]() $G\setminus \partial P$
has a unique finite component
$G\setminus \partial P$
has a unique finite component
![]() $D$
. Notice that
$D$
. Notice that
![]() $G\setminus D$
has no finite components, that is
$G\setminus D$
has no finite components, that is
![]() $\overline{D}=D$
. Now
$\overline{D}=D$
. Now
![]() $\partial P$
is the set of vertices of
$\partial P$
is the set of vertices of
![]() $G\setminus \overline{D}$
that have a neighbour in
$G\setminus \overline{D}$
that have a neighbour in
![]() $\overline{D}$
. Moreover, all vertices of
$\overline{D}$
. Moreover, all vertices of
![]() $\overline{D}$
which have a neighbour not in
$\overline{D}$
which have a neighbour not in
![]() $\overline{D}$
belong to
$\overline{D}$
belong to
![]() $P$
. On the other hand, each vertex
$P$
. On the other hand, each vertex
![]() $u$
of
$u$
of
![]() $P$
has a neighbour in
$P$
has a neighbour in
![]() $\partial P$
because there is a
$\partial P$
because there is a
![]() $\mathcal{P}$
-path connecting
$\mathcal{P}$
-path connecting
![]() $u$
to
$u$
to
![]() $\partial P$
and
$\partial P$
and
![]() $G$
satisfies (4).
$G$
satisfies (4).
Let
![]() $L$
be the set of edges with one end vertex in
$L$
be the set of edges with one end vertex in
![]() $P$
and another in
$P$
and another in
![]() $\partial P$
, and let
$\partial P$
, and let
![]() $Q$
be the set of edges
$Q$
be the set of edges
![]() $e$
in
$e$
in
![]() $E(D)$
such that there is a
$E(D)$
such that there is a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G\setminus L$
connecting
$G\setminus L$
connecting
![]() $e$
to
$e$
to
![]() $\vec{L^{D}}$
. If
$\vec{L^{D}}$
. If
![]() $e$
is an edge in
$e$
is an edge in
![]() $Q$
, then both its end vertices are incident with an edge in
$Q$
, then both its end vertices are incident with an edge in
![]() $L$
; hence, both of them lie in
$L$
; hence, both of them lie in
![]() $P$
, because
$P$
, because
![]() $\mathcal{P}$
contains only triangles, and
$\mathcal{P}$
contains only triangles, and
![]() $D$
is an induced subgraph. It suffices to show that
$D$
is an induced subgraph. It suffices to show that
![]() $(Q,L)$
is the interface of
$(Q,L)$
is the interface of
![]() $D$
, as this will immediately imply that
$D$
, as this will immediately imply that
![]() $(P,\partial P)$
is the corresponding site interface of
$(P,\partial P)$
is the corresponding site interface of
![]() $D$
.
$D$
.
It is easy to verify that
![]() $L$
satisfies the first two items of Definition 3.6 and that
$L$
satisfies the first two items of Definition 3.6 and that
![]() $Q$
satisfies the last item of the definition. It remains to prove that
$Q$
satisfies the last item of the definition. It remains to prove that
![]() $\vec{L^{D}}$
is
$\vec{L^{D}}$
is
![]() $L$
-connected. Assuming not, we find a proper bipartition
$L$
-connected. Assuming not, we find a proper bipartition
![]() $(L_1,L_2)$
of
$(L_1,L_2)$
of
![]() $L$
, such that no
$L$
, such that no
![]() $\mathcal{P}$
-path connects
$\mathcal{P}$
-path connects
![]() $L_1$
with
$L_1$
with
![]() $L_2$
. Consider
$L_2$
. Consider
![]() $e\in L_1$
and
$e\in L_1$
and
![]() $f\in L_2$
. Then, there are two paths connecting
$f\in L_2$
. Then, there are two paths connecting
![]() $e$
with
$e$
with
![]() $f$
, where one of them lies in
$f$
, where one of them lies in
![]() $D$
and the other one lies in the complement of
$D$
and the other one lies in the complement of
![]() $D$
. The union of the two paths with
$D$
. The union of the two paths with
![]() $e$
and
$e$
and
![]() $f$
is a cycle, which we denote
$f$
is a cycle, which we denote
![]() $K$
.
$K$
.
Since
![]() $\mathcal{P}$
is a basis for the cycle space
$\mathcal{P}$
is a basis for the cycle space
![]() ${\mathcal{C}}(G)$
,
${\mathcal{C}}(G)$
,
![]() $K$
can be expressed as a sum
$K$
can be expressed as a sum
![]() $\sum C_i$
of cycles
$\sum C_i$
of cycles
![]() $C_i\in \mathcal{P}$
. Let
$C_i\in \mathcal{P}$
. Let
![]() $L_{C_i}\,:\!= \overleftrightarrow{L \cap E(C)}$
be the directions of edges of
$L_{C_i}\,:\!= \overleftrightarrow{L \cap E(C)}$
be the directions of edges of
![]() $L$
appearing in
$L$
appearing in
![]() $C_i$
. Note that no cycle
$C_i$
. Note that no cycle
![]() $C_i$
contains a path in
$C_i$
contains a path in
![]() $G\setminus L$
connecting
$G\setminus L$
connecting
![]() $L_1$
to
$L_1$
to
![]() $L_2$
, because no such path exists by the choice of
$L_2$
, because no such path exists by the choice of
![]() $(L_1,L_2)$
. Consequently,
$(L_1,L_2)$
. Consequently,
![]() $L_{C_i}$
has an even number of its elements in each of
$L_{C_i}$
has an even number of its elements in each of
![]() $L_1,L_2$
, because each component of
$L_1,L_2$
, because each component of
![]() $C_i\setminus L$
(which is a subpath of
$C_i\setminus L$
(which is a subpath of
![]() $C_i$
) is incident with either 0 or 2 such elements pointing towards the component, and they lie both in
$C_i$
) is incident with either 0 or 2 such elements pointing towards the component, and they lie both in
![]() $L_1$
or both in
$L_1$
or both in
![]() $L_2$
or both in none of the two.
$L_2$
or both in none of the two.
This leads into a contradiction by a parity argument: notice that our cycle
![]() $K$
contains an odd number of directions of edges in each of
$K$
contains an odd number of directions of edges in each of
![]() $L_1,L_2$
, namely exactly one in each –
$L_1,L_2$
, namely exactly one in each –
![]() $e$
and
$e$
and
![]() $f$
respectively – because
$f$
respectively – because
![]() $P$
avoids
$P$
avoids
![]() $L$
and
$L$
and
![]() $Q$
avoids
$Q$
avoids
![]() $D$
, hence
$D$
, hence
![]() $\vec{L^{D}}$
, by definition. But then, our equality
$\vec{L^{D}}$
, by definition. But then, our equality
![]() $K=\sum C_i$
is impossible by the above claim because sums in
$K=\sum C_i$
is impossible by the above claim because sums in
![]() ${\mathcal{C}}(G)$
preserve the parity of the number of (directed) edges in any set. This contradiction proves our statement.
${\mathcal{C}}(G)$
preserve the parity of the number of (directed) edges in any set. This contradiction proves our statement.
Most of the time, we will write
![]() $P$
instead of
$P$
instead of
![]() $(P,\partial P)$
to simplify the notation.
$(P,\partial P)$
to simplify the notation.
4. Growth rates
In this section, we give the formal definition of
![]() $b_r$
in its bond and site version, obtain some basic facts about it, and establish the connection to percolation.
$b_r$
in its bond and site version, obtain some basic facts about it, and establish the connection to percolation.
Given a graph
![]() $G$
, we let
$G$
, we let
![]() $I_{n,r,\epsilon }=I_{n,r,\epsilon }(G)$
denote the set of interfaces
$I_{n,r,\epsilon }=I_{n,r,\epsilon }(G)$
denote the set of interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
and
$|P|=n$
and
![]() $(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
. Here,
$(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
. Here,
![]() $|\!\cdot\! |$
counts the number of edges. Similarly, we let
$|\!\cdot\! |$
counts the number of edges. Similarly, we let
![]() $MI_{n,r,\epsilon }=MI_{n,r,\epsilon } (G)$
denote the set of multi-interfaces
$MI_{n,r,\epsilon }=MI_{n,r,\epsilon } (G)$
denote the set of multi-interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
and
$|P|=n$
and
![]() $(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
.
$(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
.
To avoid introducing a cumbersome notation, we will still write
![]() $I_{n,r,\epsilon }$
and
$I_{n,r,\epsilon }$
and
![]() $MI_{n,r,\epsilon }$
for the site interfaces and site multi-interfaces, respectively, of size
$MI_{n,r,\epsilon }$
for the site interfaces and site multi-interfaces, respectively, of size
![]() $n$
and boundary size between
$n$
and boundary size between
![]() $(r-\epsilon )n$
and
$(r-\epsilon )n$
and
![]() $(r+\epsilon )n$
. Moreover, we will write
$(r+\epsilon )n$
. Moreover, we will write
![]() $c_{n,r,\epsilon }^\circ$
and
$c_{n,r,\epsilon }^\circ$
and
![]() $c_{n,r,\epsilon }^\odot$
for the cardinality of
$c_{n,r,\epsilon }^\odot$
for the cardinality of
![]() $I_{n,r,\epsilon }$
and
$I_{n,r,\epsilon }$
and
![]() $MI_{n,r,\epsilon }$
, respectively.
$MI_{n,r,\epsilon }$
, respectively.
The definitions, results, and proofs that follow apply to both (bond)interfaces and site interfaces unless otherwise stated.
Definition 4.1.
Define the (upper) exponential growth rate
![]() $b_r^\circ (G)$
of the (bond or site) interfaces of
$b_r^\circ (G)$
of the (bond or site) interfaces of
![]() $G$
with surface-to-volume ratio
$G$
with surface-to-volume ratio
![]() $r$
by
$r$
by
Similarly, we define the (upper) exponential growth rate
![]() $b_r^\circ (G)$
of the (site)multi-interfaces of
$b_r^\circ (G)$
of the (site)multi-interfaces of
![]() $G$
with surface-to-volume ratio
$G$
with surface-to-volume ratio
![]() $r$
by
$r$
by
We remark that in Hammond’s definition of the exponential growth rate of lattice animals with surface-to-volume ratio
![]() $r$
,
$r$
,
![]() $\epsilon$
depends on
$\epsilon$
depends on
![]() $n$
. The above definition simplifies the proofs of some of the following results.
$n$
. The above definition simplifies the proofs of some of the following results.
We are going to study
![]() $b_r^\circ$
and
$b_r^\circ$
and
![]() $b_r^\odot$
as functions of
$b_r^\odot$
as functions of
![]() $r$
. As it turns out, these two functions coincide:
$r$
. As it turns out, these two functions coincide:
Lemma 4.2.
Let
![]() $G\in \mathcal{S}$
. Then,
$G\in \mathcal{S}$
. Then,
![]() $b_r^\circ (G) = b_r^\odot (G)$
.
$b_r^\circ (G) = b_r^\odot (G)$
.
We postpone the proof until the next section where the necessary definitions and tools are introduced.
From now on, except for the proof of Lemma 4.2, we will drop the superscripts and we will simply write
![]() $b_r$
and
$b_r$
and
![]() $c_{n,r,\epsilon }$
. In our proofs, we will work with interfaces and site interfaces instead of multi-interfaces and site multi-interfaces.
$c_{n,r,\epsilon }$
. In our proofs, we will work with interfaces and site interfaces instead of multi-interfaces and site multi-interfaces.
Similarly to
![]() $b_r$
, we define the (upper) exponential growth rate of all interfaces of
$b_r$
, we define the (upper) exponential growth rate of all interfaces of
![]() $G$
:
$G$
:
where
![]() $c_{n}(G)\,:\!= |\{\text{ interfaces $P$ with $|P|=n$} \}|$
. In the following proposition, we prove that
$c_{n}(G)\,:\!= |\{\text{ interfaces $P$ with $|P|=n$} \}|$
. In the following proposition, we prove that
![]() $b(G)=\max _r b_r(G)$
.
$b(G)=\max _r b_r(G)$
.
Observation 4.3.
Let
![]() $G$
be a bounded degree graph. Then, there is some
$G$
be a bounded degree graph. Then, there is some
![]() $r$
such that
$r$
such that
![]() $b(G)= b_r(G)$
.
$b(G)= b_r(G)$
.
Proof. Notice that there are no (site)interfaces
![]() $P$
with
$P$
with
![]() $|\partial P|/|P|\gt \Delta$
, where
$|\partial P|/|P|\gt \Delta$
, where
![]() $\Delta$
is the maximum degree of
$\Delta$
is the maximum degree of
![]() $G$
. Recursively subdivide the interval
$G$
. Recursively subdivide the interval
![]() $I_0\,:\!= [0,\Delta ]$
into two subintervals of equal length. At each step
$I_0\,:\!= [0,\Delta ]$
into two subintervals of equal length. At each step
![]() $j$
, one of the two subintervals
$j$
, one of the two subintervals
![]() $I_j$
of
$I_j$
of
![]() $I_{j-1}$
accounts for at least half of the (site)interfaces
$I_{j-1}$
accounts for at least half of the (site)interfaces
![]() $P$
of size
$P$
of size
![]() $n$
with
$n$
with
![]() $|\partial P|/|P|\in I_{j-1}$
for infinitely many
$|\partial P|/|P|\in I_{j-1}$
for infinitely many
![]() $n$
. Hence, there are at least
$n$
. Hence, there are at least
![]() $2^{-j} c_n$
(site)interfaces of size
$2^{-j} c_n$
(site)interfaces of size
![]() $n$
with
$n$
with
![]() $|\partial P|/|P|\in I_j$
for infinitely many
$|\partial P|/|P|\in I_j$
for infinitely many
![]() $n$
. By compactness,
$n$
. By compactness,
![]() $[0,\Delta ]$
contains an accumulation point
$[0,\Delta ]$
contains an accumulation point
![]() $r_0$
of the
$r_0$
of the
![]() $I_j, j\in{\mathbb N}$
. Notice that for every
$I_j, j\in{\mathbb N}$
. Notice that for every
![]() $\epsilon \gt 0$
, we have
$\epsilon \gt 0$
, we have
![]() $\limsup _{n\to \infty } c_{n,r_0,\epsilon }^{1/n}=b$
. Taking the limit as
$\limsup _{n\to \infty } c_{n,r_0,\epsilon }^{1/n}=b$
. Taking the limit as
![]() $\epsilon$
goes to
$\epsilon$
goes to
![]() $0$
, we obtain
$0$
, we obtain
![]() $b= b_{r_0}$
, as desired.
$b= b_{r_0}$
, as desired.
Using Theorem 3.7, we can easily obtain some bounds for
![]() $b_r$
for graphs which either satisfy a
$b_r$
for graphs which either satisfy a
![]() $d$
-dimensional isometric inequality P3 or contain a quasi-geodesic P4. In what follows, we will write
$d$
-dimensional isometric inequality P3 or contain a quasi-geodesic P4. In what follows, we will write
![]() $N_n$
for the (random) number of occurring (site)interfaces
$N_n$
for the (random) number of occurring (site)interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
in a percolation configuration
$|P|=n$
in a percolation configuration
![]() $\omega$
.
$\omega$
.
Proposition 4.4.
Let
![]() $G$
be a graph satisfying
P3
or
P4
. Let
$G$
be a graph satisfying
P3
or
P4
. Let
![]() $r\gt 0, 0\leq p\leq 1$
. Then, we have
$r\gt 0, 0\leq p\leq 1$
. Then, we have
![]() $p(1-p)^r \leq 1/b_r(G)$
.
$p(1-p)^r \leq 1/b_r(G)$
.
Proof. Let us first assume that
![]() $G$
satisfies P4. Consider a quasi-geodesic
$G$
satisfies P4. Consider a quasi-geodesic
![]() $X$
containing
$X$
containing
![]() $o$
, and let
$o$
, and let
![]() $X^+$
,
$X^+$
,
![]() $X^-$
be its two infinite subpaths starting from
$X^-$
be its two infinite subpaths starting from
![]() $o$
. Any occurring (site)interface
$o$
. Any occurring (site)interface
![]() $P$
has to contain a vertex
$P$
has to contain a vertex
![]() $x^+$
in
$x^+$
in
![]() $X^+$
, and a vertex
$X^+$
, and a vertex
![]() $x^-$
in
$x^-$
in
![]() $X^-$
(
$X^-$
(
![]() $x^+$
and
$x^+$
and
![]() $x^-$
may possibly coincide). If
$x^-$
may possibly coincide). If
![]() $|P|=n$
, then
$|P|=n$
, then
![]() $d_G(x^+,x^-)\leq n$
, because
$d_G(x^+,x^-)\leq n$
, because
![]() $P$
is a connected graph. Hence,
$P$
is a connected graph. Hence,
![]() $d_X(x^+,x^-)\leq \ell n$
, implying that
$d_X(x^+,x^-)\leq \ell n$
, implying that
![]() $x^+$
is one of the first
$x^+$
is one of the first
![]() $ln+1$
vertices of
$ln+1$
vertices of
![]() $X^+$
. Since occurring (site)interfaces are disjoint by Theorem 3.7,
$X^+$
. Since occurring (site)interfaces are disjoint by Theorem 3.7,
for every
![]() $n$
and any bond (site) percolation configuration
$n$
and any bond (site) percolation configuration
![]() $\omega$
. Therefore,
$\omega$
. Therefore,
![]() $\mathbb{E}_p(N_n)\leq \ell n+1$
for every
$\mathbb{E}_p(N_n)\leq \ell n+1$
for every
![]() $p\in [0,1]$
. We now have
$p\in [0,1]$
. We now have
![]() $\ell n+1\geq \mathbb{E}_p(N_n)\geq c_{n,r,\epsilon } (p(1-p)^{r+\epsilon })^n$
. Taking the
$\ell n+1\geq \mathbb{E}_p(N_n)\geq c_{n,r,\epsilon } (p(1-p)^{r+\epsilon })^n$
. Taking the
![]() $n$
th root, and then letting
$n$
th root, and then letting
![]() $n$
go to infinity, and
$n$
go to infinity, and
![]() $\epsilon$
go to
$\epsilon$
go to
![]() $0$
, we obtain
$0$
, we obtain
![]() $p(1-p)^r \leq 1/b_r$
, as desired.
$p(1-p)^r \leq 1/b_r$
, as desired.
If
![]() $G$
does not contain a quasi-geodesic but satisfies the isoperimetric inequality P3, then the assertion can be proved as follows. Since
$G$
does not contain a quasi-geodesic but satisfies the isoperimetric inequality P3, then the assertion can be proved as follows. Since
![]() $G$
is locally finite, it contains an
$G$
is locally finite, it contains an
![]() $1$
-way infinite path
$1$
-way infinite path
![]() $X$
starting from
$X$
starting from
![]() $o$
that does not revisit the same vertex twice. Any occurring (site)interface
$o$
that does not revisit the same vertex twice. Any occurring (site)interface
![]() $P$
has to contain one of the first
$P$
has to contain one of the first
![]() $(|P|/c)^{\frac{d}{d-1}}$
vertices of
$(|P|/c)^{\frac{d}{d-1}}$
vertices of
![]() $X$
by P3, hence
$X$
by P3, hence
![]() $N_n\leq (n/c)^{\frac{d}{d-1}}$
. Arguing as above, we obtain
$N_n\leq (n/c)^{\frac{d}{d-1}}$
. Arguing as above, we obtain
![]() $p(1-p)^r \leq 1/b_r$
.
$p(1-p)^r \leq 1/b_r$
.
Next, we observe that for any fixed
![]() $r$
, equality in Proposition 4.4 can occur for at most one value of
$r$
, equality in Proposition 4.4 can occur for at most one value of
![]() $p$
, which value we can compute:
$p$
, which value we can compute:
Proposition 4.5.
Let
![]() $G$
be a graph satisfying
P3
or
P4
. If
$G$
be a graph satisfying
P3
or
P4
. If
![]() $p(1-p)^r = 1/b_r(G)$
for some
$p(1-p)^r = 1/b_r(G)$
for some
![]() $r,p$
, then
$r,p$
, then
![]() $p=\frac 1{1+r}$
$p=\frac 1{1+r}$
![]() $\Big($
and so
$\Big($
and so
![]() $r=\frac{1-p}{p}$
and
$r=\frac{1-p}{p}$
and
![]() $1/b_r(G)= p(1-p)^{\frac{1-p}{p}}\Big)$
.
$1/b_r(G)= p(1-p)^{\frac{1-p}{p}}\Big)$
.
Proof. Fix
![]() $r$
and let
$r$
and let
![]() $M\,:\!= \max _{p\in [0,1]} p(1-p)^r$
. If
$M\,:\!= \max _{p\in [0,1]} p(1-p)^r$
. If
![]() $p_0(1-p_0)^r = 1/b_r$
is satisfied for some
$p_0(1-p_0)^r = 1/b_r$
is satisfied for some
![]() $p_0\in [0,1]$
, then
$p_0\in [0,1]$
, then
![]() $p_0$
must attain
$p_0$
must attain
![]() $M$
by Proposition 4.4, that is, we have
$M$
by Proposition 4.4, that is, we have
![]() $M= p_0(1-p_0)^r$
. Since the function
$M= p_0(1-p_0)^r$
. Since the function
![]() $f(p)= p(1-p)^r$
vanishes at the endpoints
$f(p)= p(1-p)^r$
vanishes at the endpoints
![]() $p=0,1$
, we deduce that
$p=0,1$
, we deduce that
![]() $f^{\prime}(p_0)=0$
. By elementary calculus,
$f^{\prime}(p_0)=0$
. By elementary calculus,
![]() $f^{\prime}(p)= (1-p)^r - rp(1-p)^{r-1}$
, from which we obtain
$f^{\prime}(p)= (1-p)^r - rp(1-p)^{r-1}$
, from which we obtain
![]() $r= \frac{1-p_0}{p_0}$
and
$r= \frac{1-p_0}{p_0}$
and
![]() $p_0=\frac 1{1+r}$
.
$p_0=\frac 1{1+r}$
.
Combining Proposition 4.4 and Proposition 4.5, we obtain
Motivated by Proposition 4.5, we define the functions
These functions are 1-1, strictly monotone decreasing and the inverse of each other.
Recall that
![]() $N_n$
denotes the number of occurring multi-interfaces
$N_n$
denotes the number of occurring multi-interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
. The next result says that equality is achieved in Proposition 4.5 (for some
$|P|=n$
. The next result says that equality is achieved in Proposition 4.5 (for some
![]() $r$
) exactly for those
$r$
) exactly for those
![]() $p$
for which exponential decay in
$p$
for which exponential decay in
![]() $n$
of
$n$
of
![]() $\mathbb E_p(N_n)$
fails.
$\mathbb E_p(N_n)$
fails.
Proposition 4.6.
Let
![]() $G$
be a graph satisfying
P3
or
P4
and
$G$
be a graph satisfying
P3
or
P4
and
![]() $p\in (0,1)$
. Then
$p\in (0,1)$
. Then
![]() $\mathbb E_p(N_n)$
fails to decay exponentially in
$\mathbb E_p(N_n)$
fails to decay exponentially in
![]() $n$
if and only if
$n$
if and only if
![]() $b_{r(p)}(G) = 1/p(1-p)^{r(p)}$
(that is, if and only if equality is achieved in Proposition 4.5).
$b_{r(p)}(G) = 1/p(1-p)^{r(p)}$
(that is, if and only if equality is achieved in Proposition 4.5).
For the proof of this, we will make use of a large deviation bound for
![]() $\mathbb E_p(N_n)$
. In the percolation setup of Proposition 4.6, we denote by
$\mathbb E_p(N_n)$
. In the percolation setup of Proposition 4.6, we denote by
![]() $N_{n,r(p),\epsilon }$
the (random) number of occurring (site)multi-interfaces
$N_{n,r(p),\epsilon }$
the (random) number of occurring (site)multi-interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
and
$|P|=n$
and
![]() $(r(p)-\epsilon )n \leq |\partial P| \leq (r(p)+\epsilon )n$
. The following lemma says that for any
$(r(p)-\epsilon )n \leq |\partial P| \leq (r(p)+\epsilon )n$
. The following lemma says that for any
![]() $p\in (0,1)$
, most occurring multi-interfaces have a volume-to-surface ratio close to the value
$p\in (0,1)$
, most occurring multi-interfaces have a volume-to-surface ratio close to the value
![]() $r(p)$
.
$r(p)$
.
Lemma 4.7.
Let
![]() $G$
be a graph satisfying
P3
or
P4
and
$G$
be a graph satisfying
P3
or
P4
and
![]() $p\in (0,1)$
. For every
$p\in (0,1)$
. For every
![]() $\epsilon \gt 0$
, there exists
$\epsilon \gt 0$
, there exists
![]() $\delta \gt 0$
such that
$\delta \gt 0$
such that
![]() $\mathbb E_p(N_n-N_{n,r(p),\epsilon })\leq e^{-\delta n}$
for every
$\mathbb E_p(N_n-N_{n,r(p),\epsilon })\leq e^{-\delta n}$
for every
![]() $n\in{\mathbb N}$
.
$n\in{\mathbb N}$
.
Proof. Consider the function
![]() $g(q,r)=q(1-q)^r$
. Notice that for every fixed
$g(q,r)=q(1-q)^r$
. Notice that for every fixed
![]() $r$
, the function
$r$
, the function
![]() $g_r(q)\,:\!=g(q,r)$
is maximised at
$g_r(q)\,:\!=g(q,r)$
is maximised at
![]() $\frac{1}{1+r}$
and is strictly monotone on the intervals
$\frac{1}{1+r}$
and is strictly monotone on the intervals
![]() $\big[0,\frac{1}{1+r}\big]$
and
$\big[0,\frac{1}{1+r}\big]$
and
![]() $\big[\frac{1}{1+r},1\big]$
. Recall that
$\big[\frac{1}{1+r},1\big]$
. Recall that
![]() $p=\frac{1}{1+r(p)}$
, and define
$p=\frac{1}{1+r(p)}$
, and define
and
It follows that there is a constant
![]() $0\lt c=c(p,\epsilon )\lt 1$
such that
$0\lt c=c(p,\epsilon )\lt 1$
such that
![]() $g(p,r(p)+\epsilon )\leq c g(s,r(p)+\epsilon )$
and
$g(p,r(p)+\epsilon )\leq c g(s,r(p)+\epsilon )$
and
![]() $g(p,r(p)-\epsilon )\leq c g(S,r(p)-\epsilon )$
, because
$g(p,r(p)-\epsilon )\leq c g(S,r(p)-\epsilon )$
, because
![]() $s\lt p\lt S$
. Moreover, we have
$s\lt p\lt S$
. Moreover, we have
whenever
![]() $r\geq r(p)+\epsilon$
, and
$r\geq r(p)+\epsilon$
, and
whenever
![]() $r\leq r(p)-\epsilon$
. This implies that
$r\leq r(p)-\epsilon$
. This implies that
![]() $g(p,r)\leq c g(s,r)$
for every
$g(p,r)\leq c g(s,r)$
for every
![]() $r\geq r(p)+\epsilon$
, and
$r\geq r(p)+\epsilon$
, and
![]() $g(p,r)\leq c g(S,r)$
for every
$g(p,r)\leq c g(S,r)$
for every
![]() $r\leq r(p)-\epsilon$
. Summing over all possible (site)multi-interfaces
$r\leq r(p)-\epsilon$
. Summing over all possible (site)multi-interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
and
$|P|=n$
and
![]() $|\partial P|\gt (r+\epsilon )n$
or
$|\partial P|\gt (r+\epsilon )n$
or
![]() $|\partial P|\lt (r-\epsilon )n$
gives
$|\partial P|\lt (r-\epsilon )n$
gives
Since both
![]() $\mathbb E_{s}(N_n),\mathbb E_{S}(N_n)\leq ln+1$
, we conclude that
$\mathbb E_{s}(N_n),\mathbb E_{S}(N_n)\leq ln+1$
, we conclude that
![]() $\mathbb E_p(N_n-N_{n,r(p),\epsilon })$
decays exponentially in
$\mathbb E_p(N_n-N_{n,r(p),\epsilon })$
decays exponentially in
![]() $n$
.
$n$
.
Proof of Proposition 4.6. For the backward implication, let
![]() $\varepsilon \gt 0$
and note that for every
$\varepsilon \gt 0$
and note that for every
![]() $n \geq 1$
we have
$n \geq 1$
we have
Taking
![]() $n$
-th roots and then sending
$n$
-th roots and then sending
![]() $n$
to infinity and
$n$
to infinity and
![]() $\varepsilon$
to
$\varepsilon$
to
![]() $0$
, we obtain that
$0$
, we obtain that
Thus,
![]() $\mathbb E_p(N_n)$
does not decay exponentially if
$\mathbb E_p(N_n)$
does not decay exponentially if
![]() $b_{r(p)}=1/p (1-p)^{r(p)}$
.
$b_{r(p)}=1/p (1-p)^{r(p)}$
.
For the forward implication, suppose to the contrary that
The definition of
![]() $b_r$
implies that there are
$b_r$
implies that there are
![]() $\epsilon,\delta \gt 0$
such that
$\epsilon,\delta \gt 0$
such that
for all but finitely
![]() $n$
. Hence for every large enough
$n$
. Hence for every large enough
![]() $n$
,
$n$
,
which implies the exponential decay in
![]() $n$
of
$n$
of
![]() $\mathbb E_p(N_{n,r(p),\epsilon })$
. On the other hand,
$\mathbb E_p(N_{n,r(p),\epsilon })$
. On the other hand,
![]() $\mathbb E_p(N_n-N_{n,r(p),\epsilon })$
decays exponentially in
$\mathbb E_p(N_n-N_{n,r(p),\epsilon })$
decays exponentially in
![]() $n$
by Lemma 4.7. Therefore,
$n$
by Lemma 4.7. Therefore,
![]() $\mathbb E_p(N_n)$
decays exponentially in
$\mathbb E_p(N_n)$
decays exponentially in
![]() $n$
too.
$n$
too.
Let
![]() $S_o$
denote the (site)interface of the cluster
$S_o$
denote the (site)interface of the cluster
![]() $C_o$
of
$C_o$
of
![]() $o$
if
$o$
if
![]() $C_o$
is finite, and
$C_o$
is finite, and
![]() $S_o=\emptyset$
otherwise. We can now easily deduce that the statement of Proposition 4.6 holds for
$S_o=\emptyset$
otherwise. We can now easily deduce that the statement of Proposition 4.6 holds for
![]() $P_p( |S_o|=n )$
in place of
$P_p( |S_o|=n )$
in place of
![]() $\mathbb E_p(N_n)$
, as stated in Theorem 1.2, which we repeat here for convenience:
$\mathbb E_p(N_n)$
, as stated in Theorem 1.2, which we repeat here for convenience:
Theorem 4.8.
Let
![]() $G\in \mathcal{S}$
. Then for every
$G\in \mathcal{S}$
. Then for every
![]() $p\in (0,1)$
, the cluster size distribution
$p\in (0,1)$
, the cluster size distribution
![]() ${\mathbb{P}}_p( |S_o|=n )$
fails to decay exponentially in
${\mathbb{P}}_p( |S_o|=n )$
fails to decay exponentially in
![]() $n$
if and only if
Footnote
1
$n$
if and only if
Footnote
1
Proof. Let
![]() $X$
be a quasi-geodesic containing
$X$
be a quasi-geodesic containing
![]() $o$
such that
$o$
such that
![]() $X+tv_1=X$
for some
$X+tv_1=X$
for some
![]() $t\in{\mathbb N}$
, and let
$t\in{\mathbb N}$
, and let
![]() $X^+$
be one of the two infinite subpaths of
$X^+$
be one of the two infinite subpaths of
![]() $X$
starting at
$X$
starting at
![]() $o$
. Recall the definition of
$o$
. Recall the definition of
![]() $\mathcal{S}$
in Definition 3.1. If
$\mathcal{S}$
in Definition 3.1. If
![]() $G$
is
$G$
is
![]() ${\mathbb{Z}}^d$
or
${\mathbb{Z}}^d$
or
![]() $\mathbb{T}^d$
, we just let
$\mathbb{T}^d$
, we just let
![]() $X$
be a geodesic. Notice that any (site)interface
$X$
be a geodesic. Notice that any (site)interface
![]() $P$
meets
$P$
meets
![]() $X^+$
at some vertex
$X^+$
at some vertex
![]() $x^+$
. Using a multiple
$x^+$
. Using a multiple
![]() $ktv_1$
of
$ktv_1$
of
![]() $tv_1$
for some integer
$tv_1$
for some integer
![]() $k$
, we can translate
$k$
, we can translate
![]() $x^+$
to one of the first
$x^+$
to one of the first
![]() $M$
vertices of
$M$
vertices of
![]() $X^+$
, for some fixed
$X^+$
, for some fixed
![]() $M\gt 0$
. It is not hard to see that
$M\gt 0$
. It is not hard to see that
![]() $P+ktv_1$
is a (site) interface of
$P+ktv_1$
is a (site) interface of
![]() $o$
, that is it still separates
$o$
, that is it still separates
![]() $o$
from infinity. On the event
$o$
from infinity. On the event
![]() $A=A(P)\,:\!=\{\text{$P+ktv_1$ occurs}\} \cap \{\text{the subpath of $X^+$ between $o$ and $x^+ +ktv_1$ is open}\}$
, we have
$A=A(P)\,:\!=\{\text{$P+ktv_1$ occurs}\} \cap \{\text{the subpath of $X^+$ between $o$ and $x^+ +ktv_1$ is open}\}$
, we have
![]() $S_o=P+ktv_1$
. Moreover,
$S_o=P+ktv_1$
. Moreover,
Summing over all (site)interfaces of size
![]() $n$
with the property that the first vertex of
$n$
with the property that the first vertex of
![]() $X^+$
they contain is
$X^+$
they contain is
![]() $x^+$
, we obtain
$x^+$
, we obtain
where the sum ranges over all such (site)interfaces. Since there are at most
![]() $ln+1$
choices for the first vertex of
$ln+1$
choices for the first vertex of
![]() $X^+$
, summing over all possible
$X^+$
, summing over all possible
![]() $x^+$
we obtain
$x^+$
we obtain
On the other hand, clearly
Therefore,
![]() ${\mathbb{P}}_p(|S_o|=n)$
decays exponentially if and only if
${\mathbb{P}}_p(|S_o|=n)$
decays exponentially if and only if
![]() $\mathbb E_p(X_n)$
does. The desired assertion follows now from Proposition 4.6.
$\mathbb E_p(X_n)$
does. The desired assertion follows now from Proposition 4.6.
5. Duality
The main aim of this section is the proof of Theorem 1.3 (Theorem 5.1) and an analogous statement for planar bond percolation (Theorem 5.2). In this section, we study the properties of both interfaces and site interfaces of graphs in
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
If
![]() $G\in \mathcal{S}$
satisfies (4), we say that
$G\in \mathcal{S}$
satisfies (4), we say that
![]() $(P,\partial P)$
is a site inner interface of
$(P,\partial P)$
is a site inner interface of
![]() $G$
if
$G$
if
![]() $(\partial P,P)$
is a site interface of
$(\partial P,P)$
is a site interface of
![]() $G$
. In other words, any site inner interface can be obtained from an interface by exchanging the roles of occupied and vacant vertices. When clear from context, we will simply refer to
$G$
. In other words, any site inner interface can be obtained from an interface by exchanging the roles of occupied and vacant vertices. When clear from context, we will simply refer to
![]() $(P,\partial P)$
as an inner-interface.
$(P,\partial P)$
as an inner-interface.
Recall that for a site interface
![]() $(\partial P,P)$
,
$(\partial P,P)$
,
![]() $\partial P$
spans a connected graph. We claim that when (4) is satisfied, then
$\partial P$
spans a connected graph. We claim that when (4) is satisfied, then
![]() $P$
spans a connected graph too. Indeed, assume that this is not the case, and consider a set of vertices
$P$
spans a connected graph too. Indeed, assume that this is not the case, and consider a set of vertices
![]() $C \subset P$
which spans a connected graph. Then,
$C \subset P$
which spans a connected graph. Then,
![]() $(C,P\setminus C)$
is a proper bipartition of
$(C,P\setminus C)$
is a proper bipartition of
![]() $P$
; hence, there exist vertices
$P$
; hence, there exist vertices
![]() $u\in C$
,
$u\in C$
,
![]() $v \in P\setminus C$
which lie in the same triangle. In particular,
$v \in P\setminus C$
which lie in the same triangle. In particular,
![]() $u$
and
$u$
and
![]() $v$
lie in the same connected component, which is a contradiction.
$v$
lie in the same connected component, which is a contradiction.
We define
![]() $b_r^*$
similarly to
$b_r^*$
similarly to
![]() $b_r$
, except that we now count inner-interfaces instead of site interfaces. Since this operation inverts the surface-to-volume ratio, we have
$b_r$
, except that we now count inner-interfaces instead of site interfaces. Since this operation inverts the surface-to-volume ratio, we have
If
![]() $G$
is a doubly periodic planar lattice, we say that
$G$
is a doubly periodic planar lattice, we say that
![]() $(P,\partial P)$
is an inner-interface of
$(P,\partial P)$
is an inner-interface of
![]() $G$
if
$G$
if
![]() $(\partial P^*,P^*)$
is an interface of
$(\partial P^*,P^*)$
is an interface of
![]() $G^*$
. Again define
$G^*$
. Again define
![]() $b_r^*(G)$
similarly to
$b_r^*(G)$
similarly to
![]() $b_r(G)$
, except that we now count inner-interfaces in the dual lattice
$b_r(G)$
, except that we now count inner-interfaces in the dual lattice
![]() $G^*$
. Then (7) still holds in this case.
$G^*$
. Then (7) still holds in this case.
The main results of this section are:
Theorem 5.1.
Consider a graph
![]() $G\in \mathcal{S}$
satisfying (4). Then for the site interfaces in
$G\in \mathcal{S}$
satisfying (4). Then for the site interfaces in
![]() $G$
we have
$G$
we have
![]() $b_r(G)= (b_{1/r}(G))^r$
for every
$b_r(G)= (b_{1/r}(G))^r$
for every
![]() $r\gt 0$
.
$r\gt 0$
.
Theorem 5.2.
Consider a doubly periodic planar lattice
![]() $G$
. Then for the interfaces in
$G$
. Then for the interfaces in
![]() $G$
and
$G$
and
![]() $G^*$
, we have
$G^*$
, we have
![]() $b_r(G)= (b_{1/r}(G^*))^r$
for every
$b_r(G)= (b_{1/r}(G^*))^r$
for every
![]() $r\gt 0$
.
$r\gt 0$
.
To prove Theorems 5.1 and 5.2, we need the following concepts. Given a graph
![]() $G\in \mathcal{S}$
, let
$G\in \mathcal{S}$
, let
![]() $v_1,v_2,\ldots, v_d\in{\mathbb{R}}^d$
be some linearly independent vectors that preserve
$v_1,v_2,\ldots, v_d\in{\mathbb{R}}^d$
be some linearly independent vectors that preserve
![]() $G$
, and let
$G$
, and let
![]() $\mathcal{B}$
be the box determined by
$\mathcal{B}$
be the box determined by
![]() $v_1,v_2,\ldots,v_d$
. For
$v_1,v_2,\ldots,v_d$
. For
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
we can choose
$\mathbb{T}^d$
we can choose
![]() $v_1,v_2,\ldots v_d$
to be the standard basis of
$v_1,v_2,\ldots v_d$
to be the standard basis of
![]() ${\mathbb{R}}^d$
. Given a (site)interface
${\mathbb{R}}^d$
. Given a (site)interface
![]() $P$
of
$P$
of
![]() $G$
, let
$G$
, let
![]() $\mathcal{T}$
be the set of translations
$\mathcal{T}$
be the set of translations
![]() $\mathcal{B}+k_1v_1+k_2v_2+\ldots k_dv_d$
,
$\mathcal{B}+k_1v_1+k_2v_2+\ldots k_dv_d$
,
![]() $k_1,k_2,\ldots,k_d \in \mathbb{Z}$
of
$k_1,k_2,\ldots,k_d \in \mathbb{Z}$
of
![]() $\mathcal{B}$
that intersect
$\mathcal{B}$
that intersect
![]() $P\cup \partial P$
. The box
$P\cup \partial P$
. The box
![]() $B(P)$
of
$B(P)$
of
![]() $P$
is the smallest box with sides parallel to
$P$
is the smallest box with sides parallel to
![]() $v_1,v_2,\ldots,v_d$
containing
$v_1,v_2,\ldots,v_d$
containing
![]() $\mathcal{T}$
. We write
$\mathcal{T}$
. We write
![]() $|B(P)|$
for the surface area of
$|B(P)|$
for the surface area of
![]() $B(P)$
, and we call it the box size of
$B(P)$
, and we call it the box size of
![]() $P$
.
$P$
.
For every
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() $r \in{\mathbb{R}}_+$
,
$r \in{\mathbb{R}}_+$
,
![]() $\epsilon \in{\mathbb{R}}_+$
, and
$\epsilon \in{\mathbb{R}}_+$
, and
![]() $\delta \in{\mathbb{R}}_+$
let
$\delta \in{\mathbb{R}}_+$
let
![]() $c_{n,r,\epsilon,\delta }(G)$
denote the number of interfaces
$c_{n,r,\epsilon,\delta }(G)$
denote the number of interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
,
$|P|=n$
,
![]() $(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
and
$(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
and
![]() $|B(P)|\leq \delta n$
. We define
$|B(P)|\leq \delta n$
. We define
![]() $\widetilde b_r$
to be the exponential growth rate as
$\widetilde b_r$
to be the exponential growth rate as
![]() $\delta \to 0$
and
$\delta \to 0$
and
![]() $\epsilon \to 0$
:
$\epsilon \to 0$
:
Our aim now is to prove that
![]() $\widetilde b_r = b_r$
. In other words, (site)interfaces with a ‘fractal’ shape have the same exponential growth rate as all (site)interfaces.
$\widetilde b_r = b_r$
. In other words, (site)interfaces with a ‘fractal’ shape have the same exponential growth rate as all (site)interfaces.
We will first consider the cases of
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
.
$\mathbb{T}^d$
.
Proposition 5.3.
Let
![]() $G$
be either
$G$
be either
![]() ${\mathbb{Z}}^d$
or
${\mathbb{Z}}^d$
or
![]() $\mathbb{T}^d$
. Then
$\mathbb{T}^d$
. Then
![]() $\widetilde b_r(G) = b_r(G)$
.
$\widetilde b_r(G) = b_r(G)$
.
Proof. Let us start with an informal outline of the proof. We consider a big box which we partition by boxes
![]() $B_{\textbf{i}}$
of much smaller size chosen in a suitable way, and inside each box
$B_{\textbf{i}}$
of much smaller size chosen in a suitable way, and inside each box
![]() $B_{\textbf{i}}$
we place an interface of surface-to-volume ratio roughly
$B_{\textbf{i}}$
we place an interface of surface-to-volume ratio roughly
![]() $r$
whose box is
$r$
whose box is
![]() $B_{\textbf{i}}$
. To handle the combinatorial complexity of the set of interfaces we wish to construct, we need to choose
$B_{\textbf{i}}$
. To handle the combinatorial complexity of the set of interfaces we wish to construct, we need to choose
![]() $B_{\textbf{i}}$
so that it is the box of a big proportion of interfaces. Connecting all interfaces in a suitable way, they merge into a larger interface which has a ‘fractal’ shape. However, to show that the surface-to-volume ratio of the interface we constructed is roughly
$B_{\textbf{i}}$
so that it is the box of a big proportion of interfaces. Connecting all interfaces in a suitable way, they merge into a larger interface which has a ‘fractal’ shape. However, to show that the surface-to-volume ratio of the interface we constructed is roughly
![]() $r$
, we need to connect all the interfaces by short paths. To this end, we move around each box
$r$
, we need to connect all the interfaces by short paths. To this end, we move around each box
![]() $B_{\textbf{i}}$
so that interfaces in neighbouring boxes can be connected by short paths.
$B_{\textbf{i}}$
so that interfaces in neighbouring boxes can be connected by short paths.
We now proceed with the formal proof. We will first prove the assertion for interfaces. Let us first assume that
![]() $b_r\gt 1$
. Let
$b_r\gt 1$
. Let
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() $\epsilon \gt 0$
,
$\epsilon \gt 0$
,
![]() $r\gt 0$
, and let
$r\gt 0$
, and let
![]() $P\in I_{n,r,\epsilon }$
. Consider the box
$P\in I_{n,r,\epsilon }$
. Consider the box
![]() $B(P)$
and notice that it contains
$B(P)$
and notice that it contains
![]() $P\cup \partial P$
in its interior (no vertex of
$P\cup \partial P$
in its interior (no vertex of
![]() $P\cup \partial P$
lies in its topological boundary). Order the vertices on the boundary of the box arbitrarily. Define the shape of an interface
$P\cup \partial P$
lies in its topological boundary). Order the vertices on the boundary of the box arbitrarily. Define the shape of an interface
![]() $P$
to be the
$P$
to be the
![]() $3d$
-tuple consisting of the dimensions of the box
$3d$
-tuple consisting of the dimensions of the box
![]() $B(P)$
, and the first vertex of each of the
$B(P)$
, and the first vertex of each of the
![]() $2d$
faces of
$2d$
faces of
![]() $B(P)$
in our ordering that has distance
$B(P)$
in our ordering that has distance
![]() $1$
from
$1$
from
![]() $\partial P$
. We will call these vertices extremal. Notice that the extremal vertices are incident to a vertex in
$\partial P$
. We will call these vertices extremal. Notice that the extremal vertices are incident to a vertex in
![]() $\partial ^V P$
.
$\partial ^V P$
.
We start by showing that there is a set
![]() $K\subset I_{n,r,\epsilon }$
that has the same growth rate as
$K\subset I_{n,r,\epsilon }$
that has the same growth rate as
![]() $I_{n,r,\epsilon }$
and which consists of interfaces of the same shape. Indeed, notice that each side of
$I_{n,r,\epsilon }$
and which consists of interfaces of the same shape. Indeed, notice that each side of
![]() $B(P)$
has at most
$B(P)$
has at most
![]() $n+4$
vertices because the diameter of
$n+4$
vertices because the diameter of
![]() $P$
is at most
$P$
is at most
![]() $n$
. Once we know the box of
$n$
. Once we know the box of
![]() $P$
, there are at most
$P$
, there are at most
![]() $(n+4)^{2d(d-1)}$
possibilities for the extremal vertices; hence, there are at most
$(n+4)^{2d(d-1)}$
possibilities for the extremal vertices; hence, there are at most
![]() $q(n)\,:\!=(n+4)^{2d^2}$
possible shapes for interfaces of size
$q(n)\,:\!=(n+4)^{2d^2}$
possible shapes for interfaces of size
![]() $n$
. On the other hand, there are exponentially many interfaces in
$n$
. On the other hand, there are exponentially many interfaces in
![]() $I_{n,r,\epsilon }$
, so we can choose
$I_{n,r,\epsilon }$
, so we can choose
![]() $n$
large enough to ensure that there is a non-empty set
$n$
large enough to ensure that there is a non-empty set
![]() $K\subseteq I_{n,r,\epsilon }$
of cardinality at least
$K\subseteq I_{n,r,\epsilon }$
of cardinality at least
consisting of interfaces
![]() $P$
with
$P$
with
![]() $|P|=n$
and
$|P|=n$
and
![]() $(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
that have the same shape.
$(r-\epsilon )n \leq |\partial P| \leq (r+\epsilon )n$
that have the same shape.
With the set
![]() $K$
in our disposal, we will now describe how to piece elements of
$K$
in our disposal, we will now describe how to piece elements of
![]() $K$
together to construct several interfaces of small box size and surface-to-volume ratio which is approximately
$K$
together to construct several interfaces of small box size and surface-to-volume ratio which is approximately
![]() $r$
.
$r$
.
Recall that all interfaces in
![]() $K$
have the same shape, in particular, the same box
$K$
have the same shape, in particular, the same box
![]() $\mathcal{B}$
. Let
$\mathcal{B}$
. Let
![]() $B_n$
be a
$B_n$
be a
![]() $d$
-dimensional grid of
$d$
-dimensional grid of
![]() $n^{d(d-1)}$
adjacent copies
$n^{d(d-1)}$
adjacent copies
![]() $B_{\textbf{i}}$
,
$B_{\textbf{i}}$
,
![]() $\textbf{i}=(i_1,\ldots,i_d)$
of
$\textbf{i}=(i_1,\ldots,i_d)$
of
![]() $B$
(each side contains
$B$
(each side contains
![]() $n^{d-1}$
copies of
$n^{d-1}$
copies of
![]() $B$
). In each copy of
$B$
). In each copy of
![]() $B$
in
$B$
in
![]() $B_n$
, we place an arbitrary element of
$B_n$
, we place an arbitrary element of
![]() $K$
. We denote the element of
$K$
. We denote the element of
![]() $K$
placed in
$K$
placed in
![]() $B_{\textbf{i}}$
with
$B_{\textbf{i}}$
with
![]() $K_{\textbf{i}}$
. Write
$K_{\textbf{i}}$
. Write
![]() $S_k$
,
$S_k$
,
![]() $1\leq k\leq n^{d-1}$
for the slab containing the boxes
$1\leq k\leq n^{d-1}$
for the slab containing the boxes
![]() $B_{\textbf{i}}$
with
$B_{\textbf{i}}$
with
![]() $i_1=k$
. Our aim is to connect the interfaces inside the boxes using mostly short paths. First, consider
$i_1=k$
. Our aim is to connect the interfaces inside the boxes using mostly short paths. First, consider
![]() $S_2$
and notice that every box in
$S_2$
and notice that every box in
![]() $S_2$
shares a common face with a box in
$S_2$
shares a common face with a box in
![]() $S_1$
. We can move
$S_1$
. We can move
![]() $S_2$
using the vectors
$S_2$
using the vectors
![]() $v_2,\ldots,v_d$
in order to achieve that the ‘rightmost’ extremal vertices of
$v_2,\ldots,v_d$
in order to achieve that the ‘rightmost’ extremal vertices of
![]() $S_1$
coincide with the corresponding ‘leftmost’ extremal vertices of
$S_1$
coincide with the corresponding ‘leftmost’ extremal vertices of
![]() $S_2$
lying in a common face with them. This is possible because all interfaces in
$S_2$
lying in a common face with them. This is possible because all interfaces in
![]() $K$
have the same shape. Moving each slab
$K$
have the same shape. Moving each slab
![]() $S_k$
in turn, we can make the ‘rightmost’ and ‘leftmost’ extremal vertices of consecutive slabs coincide. We now connect all these extremal vertices with their corresponding interfaces by attaching paths of length two parallel to
$S_k$
in turn, we can make the ‘rightmost’ and ‘leftmost’ extremal vertices of consecutive slabs coincide. We now connect all these extremal vertices with their corresponding interfaces by attaching paths of length two parallel to
![]() $v_1$
. Finally, we connect the interfaces in the first slab as follows. If two boxes in the first slab share a common face, then we connect the two extremal vertices lying in the common face with a path of minimum length inside that face (hence of length
$v_1$
. Finally, we connect the interfaces in the first slab as follows. If two boxes in the first slab share a common face, then we connect the two extremal vertices lying in the common face with a path of minimum length inside that face (hence of length
![]() $O(n)$
). Also, we attach a path of length two connecting all those extremal vertices to the interface of their box (Figure 3).
$O(n)$
). Also, we attach a path of length two connecting all those extremal vertices to the interface of their box (Figure 3).

Figure 3. The interface
![]() $Q$
is in the proof of Proposition 5.3.
$Q$
is in the proof of Proposition 5.3.
This construction defines a new graph
![]() $Q$
. We claim that
$Q$
. We claim that
![]() $Q$
is an interface. Indeed, if
$Q$
is an interface. Indeed, if
![]() $d=2$
it is not hard to see that each edge of
$d=2$
it is not hard to see that each edge of
![]() $Q$
is incident to the unbounded face of
$Q$
is incident to the unbounded face of
![]() $Q$
because of the way
$Q$
because of the way
![]() $Q$
is constructed and the fact that each
$Q$
is constructed and the fact that each
![]() $K_{\textbf{i}}$
has by definition the property that all its edges lie in the unbounded component of
$K_{\textbf{i}}$
has by definition the property that all its edges lie in the unbounded component of
![]() $K_{\textbf{i}}$
. It follows that
$K_{\textbf{i}}$
. It follows that
![]() $Q$
is an interface.
$Q$
is an interface.
For
![]() $d\gt 2$
, since
$d\gt 2$
, since
![]() $Q$
is a connected graph, there is a unique interface
$Q$
is a connected graph, there is a unique interface
![]() $I$
associated with it given by Theorem 3.7. We will prove that
$I$
associated with it given by Theorem 3.7. We will prove that
![]() $Q$
coincides with
$Q$
coincides with
![]() $I$
by determining
$I$
by determining
![]() $\partial I$
. We will show this in several steps. Let
$\partial I$
. We will show this in several steps. Let
![]() $V_{\textbf{i}}$
be the set of edges in
$V_{\textbf{i}}$
be the set of edges in
![]() $G$
that are perpendicular to some edge in
$G$
that are perpendicular to some edge in
![]() $E_{\textbf{i}}\,:\!=\partial K_{\textbf{i}}\cap Q$
. Note that any edge in
$E_{\textbf{i}}\,:\!=\partial K_{\textbf{i}}\cap Q$
. Note that any edge in
![]() $V_{\textbf{i}}$
can be connected to infinity without vising
$V_{\textbf{i}}$
can be connected to infinity without vising
![]() $\partial _E Q$
because of the way
$\partial _E Q$
because of the way
![]() $Q$
is constructed. Since
$Q$
is constructed. Since
![]() $\partial I$
separates
$\partial I$
separates
![]() $Q$
from infinity, it follows that
$Q$
from infinity, it follows that
![]() $V_{\textbf{i}}\subset \partial I$
.
$V_{\textbf{i}}\subset \partial I$
.
Next we will use this fact to show that
![]() $C_{\textbf{i}}\,:\!=(\partial K_{\textbf{i}}\setminus Q)\cup V_i$
is contained in
$C_{\textbf{i}}\,:\!=(\partial K_{\textbf{i}}\setminus Q)\cup V_i$
is contained in
![]() $\partial I$
. It suffices to show that
$\partial I$
. It suffices to show that
![]() $\vec{C_{\textbf{i}}^{Q}}$
is
$\vec{C_{\textbf{i}}^{Q}}$
is
![]() $C_{\textbf{i}}$
-connected, since then
$C_{\textbf{i}}$
-connected, since then
![]() $C_{\textbf{i}}\cup \partial I$
satisfies property (iii) and the uniqueness in Theorem 3.7 implies that
$C_{\textbf{i}}\cup \partial I$
satisfies property (iii) and the uniqueness in Theorem 3.7 implies that
![]() $C_{\textbf{i}}\cup \partial I=\partial I$
. To this end, consider a directed edge
$C_{\textbf{i}}\cup \partial I=\partial I$
. To this end, consider a directed edge
![]() $\vec{e}$
in
$\vec{e}$
in
![]() $\vec{\partial K_{\textbf{i}}^{K_{\textbf{i}}}}$
that can be connected to
$\vec{\partial K_{\textbf{i}}^{K_{\textbf{i}}}}$
that can be connected to
![]() $\vec{f}\in{\vec{E_{\textbf{i}}^{K_{\textbf{i}}}}}$
with a
$\vec{f}\in{\vec{E_{\textbf{i}}^{K_{\textbf{i}}}}}$
with a
![]() $\mathcal{P}$
-path
$\mathcal{P}$
-path
![]() $\Pi$
in
$\Pi$
in
![]() $G\setminus \partial K_{\textbf{i}}$
. In the case of
$G\setminus \partial K_{\textbf{i}}$
. In the case of
![]() ${\mathbb{Z}}^d$
, extending
${\mathbb{Z}}^d$
, extending
![]() $\Pi$
by
$\Pi$
by
![]() $\vec{f}$
we obtain a
$\vec{f}$
we obtain a
![]() $\mathcal{P}$
-path connecting
$\mathcal{P}$
-path connecting
![]() $\vec{e}$
to
$\vec{e}$
to
![]() $V_{\textbf{i}}$
. If
$V_{\textbf{i}}$
. If
![]() $\vec{e}$
is a diagonal edge of
$\vec{e}$
is a diagonal edge of
![]() $\mathbb{T}^d$
, then extending
$\mathbb{T}^d$
, then extending
![]() $\Pi$
by
$\Pi$
by
![]() $\vec{f}$
we obtain a
$\vec{f}$
we obtain a
![]() $\mathcal{P}$
-path connecting
$\mathcal{P}$
-path connecting
![]() $\vec{e}$
to
$\vec{e}$
to
![]() $\overleftarrow{e}$
(in this case both end vertices of
$\overleftarrow{e}$
(in this case both end vertices of
![]() $\vec{e}$
belong to
$\vec{e}$
belong to
![]() $Q$
). Now
$Q$
). Now
![]() $\overleftarrow{e}$
can be connected to
$\overleftarrow{e}$
can be connected to
![]() $V_{\textbf{i}}$
with the trivial path of length
$V_{\textbf{i}}$
with the trivial path of length
![]() $0$
. Similarly, if
$0$
. Similarly, if
![]() $\vec{e}$
is a non-diagonal edge of
$\vec{e}$
is a non-diagonal edge of
![]() $\mathbb{T}^d$
, then
$\mathbb{T}^d$
, then
![]() $\vec{e}$
can be connected to
$\vec{e}$
can be connected to
![]() $V_{\textbf{i}}$
by concatenating two
$V_{\textbf{i}}$
by concatenating two
![]() $\mathcal{P}$
-paths. Using these observations we see that for any non-trivial bipartition
$\mathcal{P}$
-paths. Using these observations we see that for any non-trivial bipartition
![]() $(J,C_{\textbf{i}}\setminus J)$
of
$(J,C_{\textbf{i}}\setminus J)$
of
![]() $C_{\textbf{i}}$
there is a
$C_{\textbf{i}}$
there is a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G\setminus C_{\textbf{i}}$
connecting
$G\setminus C_{\textbf{i}}$
connecting
![]() $J$
to
$J$
to
![]() $C_{\textbf{i}}\setminus J$
. This shows that
$C_{\textbf{i}}\setminus J$
. This shows that
![]() $\vec{C_{\textbf{i}}^{Q}}$
is
$\vec{C_{\textbf{i}}^{Q}}$
is
![]() $C_{\textbf{i}}$
-connected, as desired.
$C_{\textbf{i}}$
-connected, as desired.
It now follows from property (ii) that
![]() $K_{\textbf{i}}\subset I$
. Since
$K_{\textbf{i}}\subset I$
. Since
![]() $I$
is connected and there is a unique path connecting different
$I$
is connected and there is a unique path connecting different
![]() $K_{\textbf{i}}$
in neighbouring boxes, the latter paths need to lie in
$K_{\textbf{i}}$
in neighbouring boxes, the latter paths need to lie in
![]() $I$
. Thus
$I$
. Thus
![]() $Q\subset I$
, which implies that
$Q\subset I$
, which implies that
![]() $Q=I$
, that is
$Q=I$
, that is
![]() $Q$
is an interface.
$Q$
is an interface.
It can be easily seen that
![]() $Q$
has size roughly
$Q$
has size roughly
![]() $n^{d(d-1)+1}$
and boundary size
$n^{d(d-1)+1}$
and boundary size
for some
![]() $\epsilon ^{\prime}=\epsilon ^{\prime}(n)$
not necessarily equal to
$\epsilon ^{\prime}=\epsilon ^{\prime}(n)$
not necessarily equal to
![]() $\epsilon$
. Clearly, we can choose
$\epsilon$
. Clearly, we can choose
![]() $\epsilon ^{\prime}=\epsilon +o(1)$
, since the number of attached edges is
$\epsilon ^{\prime}=\epsilon +o(1)$
, since the number of attached edges is
![]() $O(n^d)$
. The number of such
$O(n^d)$
. The number of such
![]() $Q$
we construct is
$Q$
we construct is
![]() $|K|^{n^{d(d-1)}}\geq N^{n^{d(d-1)}}$
, because by deleting all attached paths we recover all
$|K|^{n^{d(d-1)}}\geq N^{n^{d(d-1)}}$
, because by deleting all attached paths we recover all
![]() $K_{\textbf{i}}$
, and we have
$K_{\textbf{i}}$
, and we have
![]() $|K|$
choices for each
$|K|$
choices for each
![]() $K_{\textbf{i}}$
.
$K_{\textbf{i}}$
.
Note that each slab
![]() $S_k$
has been moved at distance at most
$S_k$
has been moved at distance at most
![]() $(k-1)n=O(n^d)$
from its original position. Hence,
$(k-1)n=O(n^d)$
from its original position. Hence,
![]() $|B(Q)|=O(n^{d(d-1)})=o(|Q|)$
. The result follows by letting
$|B(Q)|=O(n^{d(d-1)})=o(|Q|)$
. The result follows by letting
![]() $n \to \infty$
and then
$n \to \infty$
and then
![]() $\epsilon \to 0$
.
$\epsilon \to 0$
.
It remains to consider the case where
![]() $b_r=0$
or
$b_r=0$
or
![]() $b_r=1$
. If
$b_r=1$
. If
![]() $b_r=0$
, there is nothing to prove. If
$b_r=0$
, there is nothing to prove. If
![]() $b_r=1$
, then we can argue as in the case
$b_r=1$
, then we can argue as in the case
![]() $b_r\gt 1$
, except that now we place the same interface at each box of the grid.
$b_r\gt 1$
, except that now we place the same interface at each box of the grid.
Let us now consider the case of site interfaces. Let us focus on the case
![]() $b_r\gt 1$
. Let
$b_r\gt 1$
. Let
![]() $K$
be a collection of at least
$K$
be a collection of at least
![]() $N$
site interfaces of
$N$
site interfaces of
![]() $I_{n,r,\epsilon }$
, all of which have the same shape. Arguing as above, we place the elements of
$I_{n,r,\epsilon }$
, all of which have the same shape. Arguing as above, we place the elements of
![]() $K$
in a
$K$
in a
![]() $d$
-dimensional grid and we connect them in the same fashion to obtain a graph
$d$
-dimensional grid and we connect them in the same fashion to obtain a graph
![]() $Q$
. For
$Q$
. For
![]() ${\mathbb{Z}}^d$
nothing changes, since
${\mathbb{Z}}^d$
nothing changes, since
![]() $Q$
is an induced graph. However, this is not necessarily true for
$Q$
is an induced graph. However, this is not necessarily true for
![]() $\mathbb{T}^d$
because some end vertices of the attached paths are possibly incident to multiple vertices of the same site interface (even the paths of the first slab are not induced). This could potentially lead to an issue in the case that some boundary vertices cannot connect to infinity without intersecting the vertices of
$\mathbb{T}^d$
because some end vertices of the attached paths are possibly incident to multiple vertices of the same site interface (even the paths of the first slab are not induced). This could potentially lead to an issue in the case that some boundary vertices cannot connect to infinity without intersecting the vertices of
![]() $Q$
.
$Q$
.
But this is impossible in our case. Indeed, define
![]() $B^{\prime}_{\textbf{i}}$
and
$B^{\prime}_{\textbf{i}}$
and
![]() $B^{\prime\prime}_{\textbf{i}}$
to be the smallest boxes containing
$B^{\prime\prime}_{\textbf{i}}$
to be the smallest boxes containing
![]() $K_{\textbf{i}}$
and
$K_{\textbf{i}}$
and
![]() $K_{\textbf{i}} \cup \partial K_{\textbf{i}}$
, respectively. Notice that every face of
$K_{\textbf{i}} \cup \partial K_{\textbf{i}}$
, respectively. Notice that every face of
![]() $B^{\prime\prime}_{\textbf{i}}$
contains at most one vertex of
$B^{\prime\prime}_{\textbf{i}}$
contains at most one vertex of
![]() $Q$
. Hence, no boundary vertex of
$Q$
. Hence, no boundary vertex of
![]() $K_{\textbf{i}}$
lying in some face of
$K_{\textbf{i}}$
lying in some face of
![]() $B^{\prime}_{\textbf{i}}$
can be separated from infinity by the vertices of
$B^{\prime}_{\textbf{i}}$
can be separated from infinity by the vertices of
![]() $Q$
. Since any boundary vertex of
$Q$
. Since any boundary vertex of
![]() $K_{\textbf{i}}$
can be connected in
$K_{\textbf{i}}$
can be connected in
![]() $G\setminus K_{\textbf{i}}$
to the boundary of
$G\setminus K_{\textbf{i}}$
to the boundary of
![]() $B^{\prime}_{\textbf{i}}$
by Proposition 3.9, the claim follows. Thus, the graph spanned by
$B^{\prime}_{\textbf{i}}$
by Proposition 3.9, the claim follows. Thus, the graph spanned by
![]() $Q$
is a site interface, which proves that
$Q$
is a site interface, which proves that
![]() $\widetilde b_r=b_r$
for site interfaces as well.
$\widetilde b_r=b_r$
for site interfaces as well.
The above arguments can be carried out for interfaces of any doubly periodic planar lattice with only minor modifications that we will describe in Lemma 5.6. However, certain difficulties arise when studying site interfaces on an arbitrary doubly periodic planar lattice. Indeed, when we connect two site interfaces
![]() $P_1,P_2$
with a path, it is possible that some of the vertices of
$P_1,P_2$
with a path, it is possible that some of the vertices of
![]() $\partial P_1$
or
$\partial P_1$
or
![]() $\partial P_2$
are now ‘separated’ from the remaining boundary vertices, see Figure 4. In fact, it is possible that most boundary vertices have this property. To remedy this, instead of choosing arbitrarily the path that connects
$\partial P_2$
are now ‘separated’ from the remaining boundary vertices, see Figure 4. In fact, it is possible that most boundary vertices have this property. To remedy this, instead of choosing arbitrarily the path that connects
![]() $P_1$
and
$P_1$
and
![]() $P_2$
, we will choose it appropriately so that only a few of them, if any, are ‘separated’ from the remaining boundary vertices.
$P_2$
, we will choose it appropriately so that only a few of them, if any, are ‘separated’ from the remaining boundary vertices.

Figure 4. If the vertex incident to the two dashed lines is attached to the site interface, the vertices of which are depicted with big disks, then the new graph is not a site interface any more.
Lemma 5.4.
Let
![]() $G$
be a graph satisfying
P3
for some
$G$
be a graph satisfying
P3
for some
![]() $c\gt 0,d\geq 2$
. Assume that
$c\gt 0,d\geq 2$
. Assume that
![]() ${\mathcal{C}}(G)$
admits a basis consisting of cycles whose length is bounded by some
${\mathcal{C}}(G)$
admits a basis consisting of cycles whose length is bounded by some
![]() $t\gt 0$
. Let
$t\gt 0$
. Let
![]() $P$
be a site interface of
$P$
be a site interface of
![]() $G$
. Then there are
$G$
. Then there are
![]() $|\partial ^V P|-O\big(|P|^{1/4}\big)=\Omega \left(|P|^{\frac{d-1}{d}}\right)$
vertices
$|\partial ^V P|-O\big(|P|^{1/4}\big)=\Omega \left(|P|^{\frac{d-1}{d}}\right)$
vertices
![]() $u\in \partial ^V P$
such that the site interface of
$u\in \partial ^V P$
such that the site interface of
![]() $P\cup \{u\}$
has size
$P\cup \{u\}$
has size
![]() $|P|-O(|P|^{3/4})$
and boundary size
$|P|-O(|P|^{3/4})$
and boundary size
![]() $|\partial P|-O\big(|\partial P|^{3/4}\big)$
.
$|\partial P|-O\big(|\partial P|^{3/4}\big)$
.
Proof. For every
![]() $v\in \partial ^V P$
, let
$v\in \partial ^V P$
, let
![]() $P_v$
be the site interface of the connected graph
$P_v$
be the site interface of the connected graph
![]() $P\cup \{v\}$
and let
$P\cup \{v\}$
and let
![]() $Q_v\,:\!=\partial P \setminus (\partial P_v \cup \{v\})$
. Write
$Q_v\,:\!=\partial P \setminus (\partial P_v \cup \{v\})$
. Write
![]() $L$
for the edges with one endpoint in
$L$
for the edges with one endpoint in
![]() $P$
and the other in
$P$
and the other in
![]() $\partial P$
,
$\partial P$
,
![]() $E_v$
for the edges of the form
$E_v$
for the edges of the form
![]() $vw$
,
$vw$
,
![]() $w\in P$
, and
$w\in P$
, and
![]() $L_v$
for the edges with one end vertex in
$L_v$
for the edges with one end vertex in
![]() $P$
and the other in
$P$
and the other in
![]() $Q_v$
, see Figure 5. First, we claim that the
$Q_v$
, see Figure 5. First, we claim that the
![]() $Q_v$
are pairwise disjoint. Indeed, assuming that this is not true, we find a pair of distinct
$Q_v$
are pairwise disjoint. Indeed, assuming that this is not true, we find a pair of distinct
![]() $u,v$
such that
$u,v$
such that
![]() $Q_u\cap Q_v \neq \emptyset$
. Since the vertices of
$Q_u\cap Q_v \neq \emptyset$
. Since the vertices of
![]() $Q_z$
,
$Q_z$
,
![]() $z\in \{u,v\}$
do not belong to
$z\in \{u,v\}$
do not belong to
![]() $\partial P_z$
,
$\partial P_z$
,
![]() $\vec{E_{z}^{{P}}}$
separates
$\vec{E_{z}^{{P}}}$
separates
![]() $\vec{L_{z}^{{P}}}$
from the remaining edges of
$\vec{L_{z}^{{P}}}$
from the remaining edges of
![]() $\vec{L^{{P}}}$
. Hence no vertex of
$\vec{L^{{P}}}$
. Hence no vertex of
![]() $Q_z$
lies in
$Q_z$
lies in
![]() $\partial ^V P$
, as any path starting from a vertex of
$\partial ^V P$
, as any path starting from a vertex of
![]() $Q_z$
and going to infinity without intersecting
$Q_z$
and going to infinity without intersecting
![]() $P$
must intersect
$P$
must intersect
![]() $z$
. This implies that if
$z$
. This implies that if
![]() $X,Y$
are two overlapping components of
$X,Y$
are two overlapping components of
![]() $\vec{L_{u}^{{P}}}$
,
$\vec{L_{u}^{{P}}}$
,
![]() $\vec{L_{u}^{{P}}}$
, respectively, then
$\vec{L_{u}^{{P}}}$
, respectively, then
![]() $X\cup Y$
is
$X\cup Y$
is
![]() $L\setminus (E_u\cup E_v)$
-connected, and thus
$L\setminus (E_u\cup E_v)$
-connected, and thus
![]() $X,Y$
coincide. Moreover,
$X,Y$
coincide. Moreover,
![]() $X$
is connected to
$X$
is connected to
![]() $\vec{E_{u}^{{P}}}$
with a
$\vec{E_{u}^{{P}}}$
with a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G\setminus L$
, and
$G\setminus L$
, and
![]() $Y$
is connected to
$Y$
is connected to
![]() $\vec{E_{v}^{{P}}}$
with a
$\vec{E_{v}^{{P}}}$
with a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G\setminus L$
. Therefore,
$G\setminus L$
. Therefore,
![]() $u$
coincides with
$u$
coincides with
![]() $v$
, which is absurd. Hence, our claim is proved.
$v$
, which is absurd. Hence, our claim is proved.

Figure 5. The situation is in the proof of Lemma 5.4.
We can now conclude that
![]() $\sum _{v\in \partial ^V P} |Q_v|\leq |\partial P|\leq \Delta |P|$
, where
$\sum _{v\in \partial ^V P} |Q_v|\leq |\partial P|\leq \Delta |P|$
, where
![]() $\Delta$
is the maximal degree of
$\Delta$
is the maximal degree of
![]() $G$
. It follows that the number of
$G$
. It follows that the number of
![]() $v\in \partial ^V P$
such that
$v\in \partial ^V P$
such that
![]() $|Q_v|\geq |P|^{3/4}$
is at most
$|Q_v|\geq |P|^{3/4}$
is at most
![]() $\Delta |P|^{1/4}$
. By the isoperimetric inequality P3 there is
$\Delta |P|^{1/4}$
. By the isoperimetric inequality P3 there is
![]() $c\gt 0$
such that
$c\gt 0$
such that
![]() $|\partial ^V P|\geq c |P|^{\frac{d-1}{d}}$
, which implies the strict inequality
$|\partial ^V P|\geq c |P|^{\frac{d-1}{d}}$
, which implies the strict inequality
![]() $|\partial ^V P|\gt \Delta |P|^{1/4}$
whenever
$|\partial ^V P|\gt \Delta |P|^{1/4}$
whenever
![]() $|P|$
is large enough. It is clear that
$|P|$
is large enough. It is clear that
![]() $P_u$
has size
$P_u$
has size
![]() $|P|-O(|P|^{3/4})$
, because
$|P|-O(|P|^{3/4})$
, because
![]() $|P\setminus P_u|\leq \Delta ^t |Q_u|$
. The proof is now complete.
$|P\setminus P_u|\leq \Delta ^t |Q_u|$
. The proof is now complete.
The boundary vertices satisfying the property of Lemma 5.4 will be called good, and the remaining ones will be called bad.
The following lemma will be used to handle the case of site interfaces in the case of doubly periodic planar lattices.
Lemma 5.5.
Let
![]() $G$
be a doubly periodic planar lattice. Let
$G$
be a doubly periodic planar lattice. Let
![]() $P$
be a site interface of size
$P$
be a site interface of size
![]() $n$
in
$n$
in
![]() $G$
, and
$G$
, and
![]() $F\subset \partial ^V P$
. Assume that the site interface of
$F\subset \partial ^V P$
. Assume that the site interface of
![]() $P\cup F$
has size at least
$P\cup F$
has size at least
![]() $n-O(n^{3/4})$
. Then the number of site interfaces
$n-O(n^{3/4})$
. Then the number of site interfaces
![]() $P^{\prime}$
of size
$P^{\prime}$
of size
![]() $n$
such that the site interfaces of
$n$
such that the site interfaces of
![]() $P\cup F$
and
$P\cup F$
and
![]() $P^{\prime}\cup F$
coincide, is
$P^{\prime}\cup F$
coincide, is
![]() $n^{O(n^{3/4})}$
.
$n^{O(n^{3/4})}$
.
Proof. Consider a site interface
![]() $P^{\prime}$
of size
$P^{\prime}$
of size
![]() $n$
such that the site interface
$n$
such that the site interface
![]() $X$
of
$X$
of
![]() $P\cup F$
, and the site interface of
$P\cup F$
, and the site interface of
![]() $P^{\prime}\cup F$
coincide. Let
$P^{\prime}\cup F$
coincide. Let
![]() $k$
be the size of
$k$
be the size of
![]() $P^{\prime}\setminus X$
. By our assumption,
$P^{\prime}\setminus X$
. By our assumption,
![]() $k=O(n^{3/4})$
. Each connected component of
$k=O(n^{3/4})$
. Each connected component of
![]() $P^{\prime}\setminus X$
is incident to some vertex of
$P^{\prime}\setminus X$
is incident to some vertex of
![]() $P$
; hence, every vertex of
$P$
; hence, every vertex of
![]() $P^{\prime}\setminus X$
has distance
$P^{\prime}\setminus X$
has distance
![]() $O(n^{3/4})$
from
$O(n^{3/4})$
from
![]() $P$
. By the polynomial growth of
$P$
. By the polynomial growth of
![]() $G$
, the number of vertices at distance
$G$
, the number of vertices at distance
![]() $O(n^{3/4})$
from
$O(n^{3/4})$
from
![]() $P$
is at most
$P$
is at most
![]() $m$
for some
$m$
for some
![]() $m=O(n^{3/2})$
. There are
$m=O(n^{3/2})$
. There are
subsets of size
![]() $k$
containing vertices having distance at most
$k$
containing vertices having distance at most
![]() $k$
from
$k$
from
![]() $P$
. Therefore, there are
$P$
. Therefore, there are
![]() $n^{O(n^{3/4})}$
site interfaces
$n^{O(n^{3/4})}$
site interfaces
![]() $P^{\prime}$
as above.
$P^{\prime}$
as above.
In order to generalise Proposition 5.3 to all elements of
![]() $\mathcal{S}$
, we will need the following definitions. Consider a doubly periodic planar lattice
$\mathcal{S}$
, we will need the following definitions. Consider a doubly periodic planar lattice
![]() $G$
. Given two linearly independent vectors
$G$
. Given two linearly independent vectors
![]() $z,w\in{\mathbb{R}}^2$
, we write
$z,w\in{\mathbb{R}}^2$
, we write
![]() $B(z,w)$
for the box determined by
$B(z,w)$
for the box determined by
![]() $z$
and
$z$
and
![]() $w$
. Given a side
$w$
. Given a side
![]() $s$
of
$s$
of
![]() $B(z,w)$
, we write
$B(z,w)$
, we write
![]() $B^s(z,w)$
for the box that is congruent to
$B^s(z,w)$
for the box that is congruent to
![]() $B(z,w)$
and satisfies
$B(z,w)$
and satisfies
![]() $B^s(z,w)\cap B(z,w)=s$
. It is not hard to see that there are vectors
$B^s(z,w)\cap B(z,w)=s$
. It is not hard to see that there are vectors
![]() $z_1,z_2,w_1,w_2$
such that the following hold:
$z_1,z_2,w_1,w_2$
such that the following hold:
-
Both
 $z_1,w_1$
are parallel to
$z_1,w_1$
are parallel to
 $v_1$
, and both
$v_1$
, and both
 $z_2,w_2$
are parallel to
$z_2,w_2$
are parallel to
 $u_2$
.
$u_2$
. -
For every side
 $s$
of
$s$
of
 $B(z_1,z_2)$
, there are vertices
$B(z_1,z_2)$
, there are vertices
 $u\in B(z_1,z_2)$
and
$u\in B(z_1,z_2)$
and
 $v\in B^s(z_1,z_2)$
that can be connected with a path lying in
$v\in B^s(z_1,z_2)$
that can be connected with a path lying in
 $B(z_1,z_2)\cup B^s(z_1,z_2)$
.
$B(z_1,z_2)\cup B^s(z_1,z_2)$
. -
For every pair of vertices
 $u,v$
in
$u,v$
in
 $B(z_1,z_2)$
, there is a path in
$B(z_1,z_2)$
, there is a path in
 $B(w_1,w_2)$
connecting
$B(w_1,w_2)$
connecting
 $u$
to
$u$
to
 $v$
.
$v$
.
We regard the tillings
![]() $\mathcal{T}_z$
and
$\mathcal{T}_z$
and
![]() $\mathcal{T}_w$
of
$\mathcal{T}_w$
of
![]() ${\mathbb{R}}^2$
by translates of
${\mathbb{R}}^2$
by translates of
![]() $B(z_1,z_2)$
and
$B(z_1,z_2)$
and
![]() $B(w_1,w_2)$
, respectively, as graphs that are naturally isomorphic to
$B(w_1,w_2)$
, respectively, as graphs that are naturally isomorphic to
![]() ${\mathbb{Z}}^2$
.
${\mathbb{Z}}^2$
.
Lemma 5.6.
Consider a graph
![]() $G\in \mathcal{S}$
. Then
$G\in \mathcal{S}$
. Then
![]() $\widetilde b_r(G) = b_r(G)$
.
$\widetilde b_r(G) = b_r(G)$
.
Proof. We handled
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
above, so it only remains to handle doubly periodic planar lattices. We will focus on the case of site interfaces with surface-to-volume ratio
$\mathbb{T}^d$
above, so it only remains to handle doubly periodic planar lattices. We will focus on the case of site interfaces with surface-to-volume ratio
![]() $r$
such that
$r$
such that
![]() $b_r\gt 1$
, which is the hardest one.
$b_r\gt 1$
, which is the hardest one.
Let
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() $\epsilon \gt 0$
,
$\epsilon \gt 0$
,
![]() $r\gt 0$
, and let
$r\gt 0$
, and let
![]() $P\in I_{n,r,\epsilon }$
. Recall that there is a
$P\in I_{n,r,\epsilon }$
. Recall that there is a
![]() $t\gt 0$
such that the cycles in our basis of
$t\gt 0$
such that the cycles in our basis of
![]() ${\mathcal{C}}(G)$
have length at most
${\mathcal{C}}(G)$
have length at most
![]() $t$
. Consider the set of boxes in
$t$
. Consider the set of boxes in
![]() $\mathcal{T}_w$
that either intersect the
$\mathcal{T}_w$
that either intersect the
![]() $2t$
-neighbourhood of
$2t$
-neighbourhood of
![]() $P\cup \partial P$
, or they share a common face with such a box. Let
$P\cup \partial P$
, or they share a common face with such a box. Let
![]() $B^t(P)$
be the smallest box with sides parallel to
$B^t(P)$
be the smallest box with sides parallel to
![]() $w_1,w_2$
containing all these boxes. Write
$w_1,w_2$
containing all these boxes. Write
![]() $s$
for a side of
$s$
for a side of
![]() $B^t(P)$
. Order the vertices of
$B^t(P)$
. Order the vertices of
![]() $B^t(P)$
arbitrarily. Among all vertices of
$B^t(P)$
arbitrarily. Among all vertices of
![]() $\partial ^V P$
that are closest to
$\partial ^V P$
that are closest to
![]() $s$
, there is one that is minimal. The minimal vertices associated with the sides of
$s$
, there is one that is minimal. The minimal vertices associated with the sides of
![]() $B^t(P)$
are called extremal. Each extremal vertex lies in some box of
$B^t(P)$
are called extremal. Each extremal vertex lies in some box of
![]() $\mathcal{T}_z$
that is called extremal as well (in case a vertex lies in more than one boxes of
$\mathcal{T}_z$
that is called extremal as well (in case a vertex lies in more than one boxes of
![]() $T_z$
, order the boxes arbitrarily and choose the minimal one). We define the shape of a site interface
$T_z$
, order the boxes arbitrarily and choose the minimal one). We define the shape of a site interface
![]() $P$
to be the tuple comprising the dimensions of the box
$P$
to be the tuple comprising the dimensions of the box
![]() $B^t(P)$
, and the extremal vertices of
$B^t(P)$
, and the extremal vertices of
![]() $P\cup \partial P$
. Using the polynomial growth of
$P\cup \partial P$
. Using the polynomial growth of
![]() $G$
, we immediately deduce that we have polynomially many choices
$G$
, we immediately deduce that we have polynomially many choices
![]() $q(n)$
for the shape and auxiliary shape of any site interface
$q(n)$
for the shape and auxiliary shape of any site interface
![]() $P$
. We define
$P$
. We define
![]() $K$
as in the proof of Proposition 5.3.
$K$
as in the proof of Proposition 5.3.
By definition, all elements
![]() $P$
of
$P$
of
![]() $K$
have the same
$K$
have the same
![]() $B^t=B^t(P)$
. It is not hard to see that at least one of the two dimensions of
$B^t=B^t(P)$
. It is not hard to see that at least one of the two dimensions of
![]() $B^t$
is
$B^t$
is
![]() $\Omega (\sqrt{n})$
. Indeed, for every vertex
$\Omega (\sqrt{n})$
. Indeed, for every vertex
![]() $u$
of
$u$
of
![]() $G$
there is a disk of small enough radius
$G$
there is a disk of small enough radius
![]() $r_u\gt 0$
containing no other vertex except for
$r_u\gt 0$
containing no other vertex except for
![]() $u$
. The translation invariance of
$u$
. The translation invariance of
![]() $G$
implies that there are only finitely possibilities for
$G$
implies that there are only finitely possibilities for
![]() $r_u$
, hence
$r_u$
, hence
![]() $r=\inf _{u\in V} r_u\gt 0$
. It follows that
$r=\inf _{u\in V} r_u\gt 0$
. It follows that
![]() $B^t$
has area
$B^t$
has area
![]() $\Omega (n)$
because it contains
$\Omega (n)$
because it contains
![]() $n$
disjoint disks of radius
$n$
disjoint disks of radius
![]() $r$
. This implies that at least one of the two dimensions of
$r$
. This implies that at least one of the two dimensions of
![]() $B^t$
is
$B^t$
is
![]() $\Omega (\sqrt{n})$
. We can assume without loss of generality that the dimension parallel to
$\Omega (\sqrt{n})$
. We can assume without loss of generality that the dimension parallel to
![]() $v_1$
has this property.
$v_1$
has this property.
We start with a
![]() $n\times n$
grid of copies
$n\times n$
grid of copies
![]() $B_{i,j}$
of
$B_{i,j}$
of
![]() $B^t$
. We place inside every
$B^t$
. We place inside every
![]() $B_{i,j}$
a site interface
$B_{i,j}$
a site interface
![]() $K_{i,j}\in K$
. We write
$K_{i,j}\in K$
. We write
![]() $S_k$
for the
$S_k$
for the
![]() $k$
th column of the grid. Similarly to the proof of Proposition 5.3, we move every column, except for the first one, in the direction parallel to
$k$
th column of the grid. Similarly to the proof of Proposition 5.3, we move every column, except for the first one, in the direction parallel to
![]() $v_2$
in such a way that the ‘rightmost’ extremal boxes of
$v_2$
in such a way that the ‘rightmost’ extremal boxes of
![]() $S_k$
and the ‘leftmost’ extremal boxes of
$S_k$
and the ‘leftmost’ extremal boxes of
![]() $S_{k+1}$
can be connected in
$S_{k+1}$
can be connected in
![]() $\mathcal{T}_z$
by a straight path parallel to
$\mathcal{T}_z$
by a straight path parallel to
![]() $v_1$
.
$v_1$
.
For every pair
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
of consecutive interfaces, there is an induced path in
$K_{i,j+1}$
of consecutive interfaces, there is an induced path in
![]() $G$
of bounded length connecting their ‘rightmost’ and ‘leftmost’ extremal vertices. We can further assume that the path lies in
$G$
of bounded length connecting their ‘rightmost’ and ‘leftmost’ extremal vertices. We can further assume that the path lies in
![]() $B_{i,j}\cup B_{i,j+1}$
by our choice of
$B_{i,j}\cup B_{i,j+1}$
by our choice of
![]() $z_1,z_2,w_1,w_2$
and the definition of
$z_1,z_2,w_1,w_2$
and the definition of
![]() $B^t$
. Indeed, if
$B^t$
. Indeed, if
![]() $\Pi =B_1,B_2,\ldots,B_l$
is a straight path in
$\Pi =B_1,B_2,\ldots,B_l$
is a straight path in
![]() $\mathcal{T}_z$
connecting the ‘rightmost’ and ‘leftmost’ extremal boxes of
$\mathcal{T}_z$
connecting the ‘rightmost’ and ‘leftmost’ extremal boxes of
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
, respectively, we first connect all consecutive boxes
$K_{i,j+1}$
, respectively, we first connect all consecutive boxes
![]() $B_m,B_{m+1}$
,
$B_m,B_{m+1}$
,
![]() $m=1,\ldots,l-1$
using paths
$m=1,\ldots,l-1$
using paths
![]() $\Pi _m$
in
$\Pi _m$
in
![]() $G$
lying in
$G$
lying in
![]() $B_m\cup B_{m+1}$
. Then we connect the ‘rightmost’ and ‘leftmost’ end vertices of consecutive paths
$B_m\cup B_{m+1}$
. Then we connect the ‘rightmost’ and ‘leftmost’ end vertices of consecutive paths
![]() $\Pi _m$
,
$\Pi _m$
,
![]() $\Pi _{m+1}$
, respectively, using paths lying in boxes congruent to
$\Pi _{m+1}$
, respectively, using paths lying in boxes congruent to
![]() $B(w_1,w_2)$
containing those end vertices. Finally, we connect the ‘rightmost’ and ‘leftmost’ of
$B(w_1,w_2)$
containing those end vertices. Finally, we connect the ‘rightmost’ and ‘leftmost’ of
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
to
$K_{i,j+1}$
to
![]() $P_1$
and
$P_1$
and
![]() $P_{l-1}$
using paths lying in boxes congruent to
$P_{l-1}$
using paths lying in boxes congruent to
![]() $B(w_1,w_2)$
. In this way, we obtain a path that lies in
$B(w_1,w_2)$
. In this way, we obtain a path that lies in
![]() $B_{i,j}\cup B_{i,j+1}$
, because both
$B_{i,j}\cup B_{i,j+1}$
, because both
![]() $B_{i,j}$
,
$B_{i,j}$
,
![]() $B_{i,j+1}$
contain a ‘layer’ of boxes of
$B_{i,j+1}$
contain a ‘layer’ of boxes of
![]() $T_w$
surrounding
$T_w$
surrounding
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
. The path is not necessarily disjoint from
$K_{i,j+1}$
. The path is not necessarily disjoint from
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
but it certainly contains a subpath that is disjoint from them, and connects two boundary vertices of both site interfaces. We can choose the subpath to contain exactly two boundary vertices, one from each of the two site interfaces.
$K_{i,j+1}$
but it certainly contains a subpath that is disjoint from them, and connects two boundary vertices of both site interfaces. We can choose the subpath to contain exactly two boundary vertices, one from each of the two site interfaces.
Let
![]() $\mathcal{W}$
be the path connecting
$\mathcal{W}$
be the path connecting
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
, and let
$K_{i,j+1}$
, and let
![]() $u_1\in \partial ^V K_{i,j}$
,
$u_1\in \partial ^V K_{i,j}$
,
![]() $u_2\in \partial ^V K_{i,j+1}$
be the end vertices of
$u_2\in \partial ^V K_{i,j+1}$
be the end vertices of
![]() $\mathcal{W}$
. Adding
$\mathcal{W}$
. Adding
![]() $u_1,u_2$
to
$u_1,u_2$
to
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
may result to much smaller site interfaces. For this reason, we need to find two good boundary vertices. Consider the vertices
$K_{i,j+1}$
may result to much smaller site interfaces. For this reason, we need to find two good boundary vertices. Consider the vertices
![]() $x_1,x_2$
at distance
$x_1,x_2$
at distance
![]() $t$
from
$t$
from
![]() $u_1,u_2$
, respectively, lying in
$u_1,u_2$
, respectively, lying in
![]() $\mathcal{W}$
. Write
$\mathcal{W}$
. Write
![]() $Q_1,Q_2$
for the
$Q_1,Q_2$
for the
![]() $(t-1)$
-neighbourhood of
$(t-1)$
-neighbourhood of
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
, respectively, and notice that both
$K_{i,j+1}$
, respectively, and notice that both
![]() $\partial ^V Q_1$
,
$\partial ^V Q_1$
,
![]() $\partial ^V Q_2$
have distance
$\partial ^V Q_2$
have distance
![]() $t$
from
$t$
from
![]() $\partial K_{i,j}$
,
$\partial K_{i,j}$
,
![]() $\partial K_{i,j+1}$
, respectively. Furthermore, they coincide with the boundary of some site interface, that is the site interface of the finite connected component of their complement, and by Remark 3.8 we can connect any pair of vertices of
$\partial K_{i,j+1}$
, respectively. Furthermore, they coincide with the boundary of some site interface, that is the site interface of the finite connected component of their complement, and by Remark 3.8 we can connect any pair of vertices of
![]() $\partial ^V Q_i$
,
$\partial ^V Q_i$
,
![]() $i=1,2$
with a path lying in the
$i=1,2$
with a path lying in the
![]() $t/2$
neighbourhood of
$t/2$
neighbourhood of
![]() $\partial ^V Q_i$
, hence disjoint from
$\partial ^V Q_i$
, hence disjoint from
![]() $K_{i,j}$
,
$K_{i,j}$
,
![]() $K_{i,j+1}$
and their boundaries. The isoperimetric inequality P3 gives
$K_{i,j+1}$
and their boundaries. The isoperimetric inequality P3 gives
![]() $\partial ^V Q_i=\Omega (\sqrt{n})$
. Moreover, for every
$\partial ^V Q_i=\Omega (\sqrt{n})$
. Moreover, for every
![]() $k\gt 0$
, the number of vertices of
$k\gt 0$
, the number of vertices of
![]() $\partial ^V Q_i$
that can be connected to
$\partial ^V Q_i$
that can be connected to
![]() $x_i$
with a path of length at most
$x_i$
with a path of length at most
![]() $k$
lying in the
$k$
lying in the
![]() $t/2$
-neighbourhood of
$t/2$
-neighbourhood of
![]() $\partial ^V Q_i$
is
$\partial ^V Q_i$
is
![]() $\Omega (k)$
. On the other hand, Lemma 5.4 implies that
$\Omega (k)$
. On the other hand, Lemma 5.4 implies that
![]() $O(n^{1/4})$
boundary vertices of either
$O(n^{1/4})$
boundary vertices of either
![]() $K_{i,j},K_{i,j+1}$
are bad. Hence choosing
$K_{i,j},K_{i,j+1}$
are bad. Hence choosing
![]() $k=cn^{1/4}$
for some large enough constant
$k=cn^{1/4}$
for some large enough constant
![]() $c\gt 0$
, we can find two good vertices
$c\gt 0$
, we can find two good vertices
![]() $y_1,y_2$
in
$y_1,y_2$
in
![]() $\partial ^V K_{i,j},\partial ^V K_{i,j+1}$
, that can be connected to
$\partial ^V K_{i,j},\partial ^V K_{i,j+1}$
, that can be connected to
![]() $x_1,x_2$
, respectively, in the following way: we first connect
$x_1,x_2$
, respectively, in the following way: we first connect
![]() $y_i$
to some vertex of
$y_i$
to some vertex of
![]() $\partial ^V Q_i$
with a path of length
$\partial ^V Q_i$
with a path of length
![]() $t$
, and then we connect the latter vertex with a path of length
$t$
, and then we connect the latter vertex with a path of length
![]() $O(n^{1/4})$
lying in the
$O(n^{1/4})$
lying in the
![]() $t/2$
neighbourhood of
$t/2$
neighbourhood of
![]() $\partial ^V Q_i$
. Taking the union of these two paths with the subpath of
$\partial ^V Q_i$
. Taking the union of these two paths with the subpath of
![]() $\mathcal{W}$
connecting
$\mathcal{W}$
connecting
![]() $x_1$
to
$x_1$
to
![]() $x_2$
, we obtain a path of length
$x_2$
, we obtain a path of length
![]() $O(n^{1/4})$
connecting
$O(n^{1/4})$
connecting
![]() $y_1$
to
$y_1$
to
![]() $y_2$
that lies in
$y_2$
that lies in
![]() $B_{i,j}\cup B_{i,j+1}$
. We attach this path to our collection of site interfaces.
$B_{i,j}\cup B_{i,j+1}$
. We attach this path to our collection of site interfaces.
Consider now a site interface
![]() $K_{i,j}$
with
$K_{i,j}$
with
![]() $2\leq j\leq n-1$
. Notice that exactly two paths emanate from
$2\leq j\leq n-1$
. Notice that exactly two paths emanate from
![]() $\partial K_{i,j}$
, one of which has distance
$\partial K_{i,j}$
, one of which has distance
![]() $O(n^{1/4})$
from the ‘rightmost’ extremal vertex of
$O(n^{1/4})$
from the ‘rightmost’ extremal vertex of
![]() $K_{i,j}$
, and the other has distance
$K_{i,j}$
, and the other has distance
![]() $O(n^{1/4})$
from the ‘leftmost’ extremal vertex of
$O(n^{1/4})$
from the ‘leftmost’ extremal vertex of
![]() $K_{i,j}$
. The two paths may possibly overlap, separating some vertices of
$K_{i,j}$
. The two paths may possibly overlap, separating some vertices of
![]() $\partial K_{i,j}$
from infinity. However, the distance between the ‘rightmost’ and the ‘leftmost’ extremal vertex is
$\partial K_{i,j}$
from infinity. However, the distance between the ‘rightmost’ and the ‘leftmost’ extremal vertex is
![]() $\Omega (\sqrt{n})$
because the dimension of
$\Omega (\sqrt{n})$
because the dimension of
![]() $B_{i,j}$
that is parallel to
$B_{i,j}$
that is parallel to
![]() $v_1$
is
$v_1$
is
![]() $\Omega (\sqrt{n})$
. We can increase the value of
$\Omega (\sqrt{n})$
. We can increase the value of
![]() $n$
if necessary to ensure that the paths do not overlap.
$n$
if necessary to ensure that the paths do not overlap.
Moreover, we connect, as we may, the boundaries of consecutive site interfaces
![]() $K_{i,1},K_{i+1,1}$
of the first column with induced paths of length
$K_{i,1},K_{i+1,1}$
of the first column with induced paths of length
![]() $O(n)$
disjoint from any other site interface, only the end vertices of which intersect the boundary of
$O(n)$
disjoint from any other site interface, only the end vertices of which intersect the boundary of
![]() $K_{i,1},K_{i+1,1}$
.
$K_{i,1},K_{i+1,1}$
.
In this way, we obtain a graph
![]() $H$
containing all site interfaces
$H$
containing all site interfaces
![]() $K_{i,j}$
. Consider the graph spanned by
$K_{i,j}$
. Consider the graph spanned by
![]() $H$
, and let
$H$
, and let
![]() $Q$
be the site interface of this induced graph. We claim that
$Q$
be the site interface of this induced graph. We claim that
![]() $Q$
has size
$Q$
has size
![]() $n^3(1-o(1))$
, and boundary size between
$n^3(1-o(1))$
, and boundary size between
![]() $(r-\epsilon ^{\prime})|Q|$
and
$(r-\epsilon ^{\prime})|Q|$
and
![]() $(r+\epsilon ^{\prime})|Q|$
, for some
$(r+\epsilon ^{\prime})|Q|$
, for some
![]() $\epsilon ^{\prime}=\epsilon +o(1)$
. Indeed, for every site interface
$\epsilon ^{\prime}=\epsilon +o(1)$
. Indeed, for every site interface
![]() $K_{i,j}$
that does not lie in the first column, if
$K_{i,j}$
that does not lie in the first column, if
![]() $F_{i,j}\subset \partial K_{i,j}$
is the set of end vertices of the attached paths that emanate from
$F_{i,j}\subset \partial K_{i,j}$
is the set of end vertices of the attached paths that emanate from
![]() $\partial K_{i,j}$
, then the site interface of
$\partial K_{i,j}$
, then the site interface of
![]() $K_{i,j}\cup F_{i,j}$
(which has size
$K_{i,j}\cup F_{i,j}$
(which has size
![]() $n-O(n^{1/4})$
) lies in the boundary of
$n-O(n^{1/4})$
) lies in the boundary of
![]() $Q$
. Since we have
$Q$
. Since we have
![]() $n^2-n$
such
$n^2-n$
such
![]() $K_{i,j}$
, the claim follows readily.
$K_{i,j}$
, the claim follows readily.
Each column
![]() $S_k$
has been moved at distance
$S_k$
has been moved at distance
![]() $O(kn)=O(n^2)=o(|Q|)$
from its original position. Hence
$O(kn)=O(n^2)=o(|Q|)$
from its original position. Hence
![]() $|B(Q)|=o(|Q|)$
. It remains to show that the number of such
$|B(Q)|=o(|Q|)$
. It remains to show that the number of such
![]() $Q$
constructed is roughly
$Q$
constructed is roughly
![]() $N^{n^2}$
. Notice that we have not necessarily used the same paths to connect our interfaces, and so given such a
$N^{n^2}$
. Notice that we have not necessarily used the same paths to connect our interfaces, and so given such a
![]() $Q$
, we cannot immediately recover all possible sequences
$Q$
, we cannot immediately recover all possible sequences
![]() $(K_{i,j})$
giving rise to
$(K_{i,j})$
giving rise to
![]() $Q$
. Our goal is to restrict to a suitable subfamily of
$Q$
. Our goal is to restrict to a suitable subfamily of
![]() $K^{n^2}$
.
$K^{n^2}$
.
We claim that there are only subexponentially many in
![]() $n^3$
possibilities for the attached paths. Recall that all elements of
$n^3$
possibilities for the attached paths. Recall that all elements of
![]() $K$
have the same extremal vertices. The end vertices of every attached path have distance
$K$
have the same extremal vertices. The end vertices of every attached path have distance
![]() $O(n^{1/4})$
from a pair of extremal vertices. Using the polynomial growth of
$O(n^{1/4})$
from a pair of extremal vertices. Using the polynomial growth of
![]() $G$
, we conclude that there are only polynomially many choices in
$G$
, we conclude that there are only polynomially many choices in
![]() $n$
for each end vertex. Moreover, the paths connecting interfaces of the first column have length
$n$
for each end vertex. Moreover, the paths connecting interfaces of the first column have length
![]() $O(n)$
, and the remaining paths have length
$O(n)$
, and the remaining paths have length
![]() $O(n^{1/4})$
. There are at most
$O(n^{1/4})$
. There are at most
![]() $\Delta ^{O(n)}$
choices for each path connecting site interfaces of the first column, and at most
$\Delta ^{O(n)}$
choices for each path connecting site interfaces of the first column, and at most
![]() $\Delta ^{O(n^{1/4})}$
choices for each of the remaining paths, because any path starting from a fixed vertex can be constructed sequentially, and there are at most
$\Delta ^{O(n^{1/4})}$
choices for each of the remaining paths, because any path starting from a fixed vertex can be constructed sequentially, and there are at most
![]() $\Delta$
choices at each step. In total, there are
$\Delta$
choices at each step. In total, there are
![]() $\Delta ^{O(n^{9/4})}$
possibilities for the attached paths. This proves our claim.
$\Delta ^{O(n^{9/4})}$
possibilities for the attached paths. This proves our claim.
On the other hand, there are at least
![]() $N^{n^2}$
sequences
$N^{n^2}$
sequences
![]() $(K_{i,j})\in K^{n^2}$
, hence for a subfamily of
$(K_{i,j})\in K^{n^2}$
, hence for a subfamily of
![]() $K^{n^2}$
of size at least
$K^{n^2}$
of size at least
![]() $N^{n^2}/{\Delta ^{O(n^{9/4})}}$
, we have used exactly the same paths. Let us restrict to that subfamily. Since we have fixed the paths connecting the elements of the subfamily, given some
$N^{n^2}/{\Delta ^{O(n^{9/4})}}$
, we have used exactly the same paths. Let us restrict to that subfamily. Since we have fixed the paths connecting the elements of the subfamily, given some
![]() $Q$
constructed by the elements of that subfamily, we can now delete every vertex of the attached paths except for their end vertices to ‘almost’ reconstruct all site interfaces producing
$Q$
constructed by the elements of that subfamily, we can now delete every vertex of the attached paths except for their end vertices to ‘almost’ reconstruct all site interfaces producing
![]() $Q$
. To be more precise, if
$Q$
. To be more precise, if
![]() $(K_{i,j})$
and
$(K_{i,j})$
and
![]() $(K^{\prime}_{i,j})$
are two sequences producing the same
$(K^{\prime}_{i,j})$
are two sequences producing the same
![]() $Q$
, then the site interfaces of
$Q$
, then the site interfaces of
![]() $K_{i,j}\cup F_{i,j}$
and
$K_{i,j}\cup F_{i,j}$
and
![]() $K^{\prime}_{i,j}\cup F_{i,j}$
coincide. By Lemma 5.5, if we fix a sequence
$K^{\prime}_{i,j}\cup F_{i,j}$
coincide. By Lemma 5.5, if we fix a sequence
![]() $(K_{i,j})$
producing
$(K_{i,j})$
producing
![]() $Q$
, then for each
$Q$
, then for each
![]() $i,j$
with
$i,j$
with
![]() $j\gt 1$
, there are subexponentially many in
$j\gt 1$
, there are subexponentially many in
![]() $n$
possible
$n$
possible
![]() $K^{\prime}_{i,j}$
as above. For each of the remaining
$K^{\prime}_{i,j}$
as above. For each of the remaining
![]() $i,j$
there are at most exponentially many in
$i,j$
there are at most exponentially many in
![]() $n$
$n$
![]() $K^{\prime}_{i,j}$
as above, since there are at most exponentially many site interfaces in total. Therefore, each
$K^{\prime}_{i,j}$
as above, since there are at most exponentially many site interfaces in total. Therefore, each
![]() $Q$
can be constructed by subexponentially many in
$Q$
can be constructed by subexponentially many in
![]() $n^3$
sequences. We can now deduce that we constructed roughly
$n^3$
sequences. We can now deduce that we constructed roughly
![]() $N^{n^2}$
$N^{n^2}$
![]() $Q$
, and taking limits we obtain
$Q$
, and taking limits we obtain
![]() $\widetilde b_r = b_r$
, as desired.
$\widetilde b_r = b_r$
, as desired.
We can now prove the main results of this section.
Proof of Theorem 5.1
. Assume first that both
![]() $b_r$
and
$b_r$
and
![]() $b_{1/r}$
are not
$b_{1/r}$
are not
![]() $0$
. We start by proving that
$0$
. We start by proving that
Combined with (7) this will easily yield the desired equality.
Assume that
![]() $G$
is a doubly periodic planar lattice. Let
$G$
is a doubly periodic planar lattice. Let
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() $r\gt 0$
,
$r\gt 0$
,
![]() $\epsilon \gt 0$
, and choose
$\epsilon \gt 0$
, and choose
![]() $P\in I_{n,r,\epsilon }$
. By Proposition 5.6, we may assume that
$P\in I_{n,r,\epsilon }$
. By Proposition 5.6, we may assume that
![]() $P$
satisfies
$P$
satisfies
![]() $|B(P)| = o(|P|)=o(n)$
. Recall that
$|B(P)| = o(|P|)=o(n)$
. Recall that
![]() $B(P)$
contains
$B(P)$
contains
![]() $P\cup \partial P$
in its interior. It is not hard to see that there is a cycle
$P\cup \partial P$
in its interior. It is not hard to see that there is a cycle
![]() $C$
at bounded distance from
$C$
at bounded distance from
![]() $P$
that separates
$P$
that separates
![]() $B(P)$
from infinity and has size
$B(P)$
from infinity and has size
![]() $O(|B(P)|)$
. Arguing as in the proof of Lemma 5.6 we find a good vertex
$O(|B(P)|)$
. Arguing as in the proof of Lemma 5.6 we find a good vertex
![]() $u\in \partial ^V P$
, and an induced path
$u\in \partial ^V P$
, and an induced path
![]() $\Pi$
connecting
$\Pi$
connecting
![]() $u$
to
$u$
to
![]() $C$
that has size
$C$
that has size
![]() $O(n^{1/4})$
, and does not contain any other vertex of
$O(n^{1/4})$
, and does not contain any other vertex of
![]() $P\cup \partial P$
.
$P\cup \partial P$
.

Figure 6. The vertices of
![]() $Q$
are depicted with big disks, and the vertices of
$Q$
are depicted with big disks, and the vertices of
![]() $\partial Q$
are depicted with smaller disks. The edges spanned by
$\partial Q$
are depicted with smaller disks. The edges spanned by
![]() $P$
and
$P$
and
![]() $C$
are depicted in solid lines, while the edges of
$C$
are depicted in solid lines, while the edges of
![]() $\Pi$
are depicted in dashed lines.
$\Pi$
are depicted in dashed lines.
Our aim now is to find a suitable inner-interface containing the site interface of
![]() $P\cup \{u\}$
, which we denote by
$P\cup \{u\}$
, which we denote by
![]() $X$
. Since the cycle space of
$X$
. Since the cycle space of
![]() $G$
is generated by its triangles,
$G$
is generated by its triangles,
![]() $\partial ^V P$
spans a cycle surrounding
$\partial ^V P$
spans a cycle surrounding
![]() $P$
and the remaining boundary vertices. Hence
$P$
and the remaining boundary vertices. Hence
![]() $\partial ^V P \setminus \{u\}$
spans a connected graph. The graph
$\partial ^V P \setminus \{u\}$
spans a connected graph. The graph
![]() $\Gamma \,:\!=X\cup \Pi \cup C$
surrounds an open subset of the plane that contains
$\Gamma \,:\!=X\cup \Pi \cup C$
surrounds an open subset of the plane that contains
![]() $\partial ^V P \setminus \{u\}$
. Consider the connected component
$\partial ^V P \setminus \{u\}$
. Consider the connected component
![]() $Y$
of
$Y$
of
![]() $\partial ^V P \setminus \{u\}$
in this open set. Write
$\partial ^V P \setminus \{u\}$
in this open set. Write
![]() $Q$
for the inner-interface of
$Q$
for the inner-interface of
![]() $Y$
, that is the boundary of the site interface of
$Y$
, that is the boundary of the site interface of
![]() $Y$
, see Figure 6.
$Y$
, see Figure 6.
We claim that
![]() $Q$
contains
$Q$
contains
![]() $X$
and is contained in
$X$
and is contained in
![]() $X\cup \Pi \cup C$
. To see that
$X\cup \Pi \cup C$
. To see that
![]() $Q$
contains
$Q$
contains
![]() $X$
, notice that all vertices of
$X$
, notice that all vertices of
![]() $X$
are incident to
$X$
are incident to
![]() $Y$
because
$Y$
because
![]() $G$
is a triangulation, and lie in the external face of
$G$
is a triangulation, and lie in the external face of
![]() $Y$
. Therefore,
$Y$
. Therefore,
![]() $X$
is contained in
$X$
is contained in
![]() $Q$
. Moreover, if
$Q$
. Moreover, if
![]() $Q$
contains some vertex not in
$Q$
contains some vertex not in
![]() $X\cup \Pi \cup C$
, then we can add this vertex to
$X\cup \Pi \cup C$
, then we can add this vertex to
![]() $Y$
to obtain an even larger connected graph. This contradiction shows that there is no such vertex and proves our claim.
$Y$
to obtain an even larger connected graph. This contradiction shows that there is no such vertex and proves our claim.
We now consider the case where
![]() $G=\mathbb{T}^d$
. We can let
$G=\mathbb{T}^d$
. We can let
![]() $C$
be the set of vertices in the boundary of
$C$
be the set of vertices in the boundary of
![]() $B(P)$
, and
$B(P)$
, and
![]() $\Pi$
be a path of length
$\Pi$
be a path of length
![]() $2$
connecting an extremal vertex of
$2$
connecting an extremal vertex of
![]() $B(P)$
to
$B(P)$
to
![]() $P$
. Let
$P$
. Let
![]() $Y$
be the subgraph of
$Y$
be the subgraph of
![]() $G$
surrounded by
$G$
surrounded by
![]() $P\cup \Pi \cup \partial C$
. It is clear that
$P\cup \Pi \cup \partial C$
. It is clear that
![]() $Y$
is connected. Write
$Y$
is connected. Write
![]() $Q$
for the inner-interface of
$Q$
for the inner-interface of
![]() $Y$
. Every vertex of
$Y$
. Every vertex of
![]() $P$
is incident to
$P$
is incident to
![]() $Y$
and lies in the infinite component of
$Y$
and lies in the infinite component of
![]() $G\setminus Y$
. Hence
$G\setminus Y$
. Hence
![]() $P$
lies in
$P$
lies in
![]() $Q$
. Furthermore,
$Q$
. Furthermore,
![]() $Q$
contains only vertices of
$Q$
contains only vertices of
![]() $X\cup \Pi \cup \partial C$
.
$X\cup \Pi \cup \partial C$
.
In both cases,
![]() $Q$
has roughly
$Q$
has roughly
![]() $n$
vertices and surface-to-volume ratio between
$n$
vertices and surface-to-volume ratio between
![]() $(r-\epsilon ^{\prime})|Q|$
and
$(r-\epsilon ^{\prime})|Q|$
and
![]() $(r+\epsilon ^{\prime})|Q|$
for some
$(r+\epsilon ^{\prime})|Q|$
for some
![]() $\epsilon ^{\prime}=\epsilon +o(1)$
. Moreover, each
$\epsilon ^{\prime}=\epsilon +o(1)$
. Moreover, each
![]() $Q$
can be obtained from only subexponentially many
$Q$
can be obtained from only subexponentially many
![]() $P$
. This proves (8). Combining this with (7), we obtain the following:
$P$
. This proves (8). Combining this with (7), we obtain the following:
where both inequalities coincide with (8) and both equalities with (7). Thus we must have equality all along, and in particular
![]() $b_r = b_{1/r}^r$
.
$b_r = b_{1/r}^r$
.
If
![]() $b_r$
or
$b_r$
or
![]() $b_{1/r}$
is equal to
$b_{1/r}$
is equal to
![]() $0$
, then the same argument shows that both
$0$
, then the same argument shows that both
![]() $b_r$
and
$b_r$
and
![]() $b_{1/r}$
are equal to
$b_{1/r}$
are equal to
![]() $0$
. This completes the proof.
$0$
. This completes the proof.
We now prove Theorem 5.2.
Proof of Theorem 5.2. Assume first that both
![]() $b_r$
and
$b_r$
and
![]() $b_{1/r}$
are not
$b_{1/r}$
are not
![]() $0$
. Choose
$0$
. Choose
![]() $P\in I_{n,r,\epsilon }$
such that
$P\in I_{n,r,\epsilon }$
such that
![]() $|B(P)| = o(|P|)=o(n)$
. Consider a cycle
$|B(P)| = o(|P|)=o(n)$
. Consider a cycle
![]() $C$
as in the proof of Theorem 5.1 and connect
$C$
as in the proof of Theorem 5.1 and connect
![]() $\partial P$
to
$\partial P$
to
![]() $C$
with a path
$C$
with a path
![]() $\Pi$
of minimal length. Notice that
$\Pi$
of minimal length. Notice that
![]() $(\partial ^E P)^*$
is a cycle, hence every
$(\partial ^E P)^*$
is a cycle, hence every
![]() $(\partial P \setminus E(\Pi ))^*$
is a connected graph.
$(\partial P \setminus E(\Pi ))^*$
is a connected graph.
Let
![]() $X$
be the connected component of
$X$
be the connected component of
![]() $(\partial P \setminus E(\Pi ))^*$
in
$(\partial P \setminus E(\Pi ))^*$
in
![]() $G^*$
that is surrounded by
$G^*$
that is surrounded by
![]() $P\cup \Pi \cup C$
, and let
$P\cup \Pi \cup C$
, and let
![]() $Q$
be the interface of
$Q$
be the interface of
![]() $X$
. Arguing as in the proof of Theorem 5.1, we see that
$X$
. Arguing as in the proof of Theorem 5.1, we see that
![]() $P^*$
lies in
$P^*$
lies in
![]() $\partial Q$
,
$\partial Q$
,
![]() $Q$
has size roughly
$Q$
has size roughly
![]() $n$
, and
$n$
, and
![]() $(r-\epsilon ^{\prime})|Q|\leq |\partial Q|\leq (r+\epsilon ^{\prime})|Q|$
for some
$(r-\epsilon ^{\prime})|Q|\leq |\partial Q|\leq (r+\epsilon ^{\prime})|Q|$
for some
![]() $\epsilon ^{\prime}=\epsilon +o(1)$
.
$\epsilon ^{\prime}=\epsilon +o(1)$
.
Let
![]() $b^\bullet _r(G)$
be defined like
$b^\bullet _r(G)$
be defined like
![]() $b_r(G)$
except that we now consider inner interfaces. Thus we have
$b_r(G)$
except that we now consider inner interfaces. Thus we have
by the definitions. The above construction now yields the inequality
![]() $b^\bullet _r(G) \geq b_r(G)$
.
$b^\bullet _r(G) \geq b_r(G)$
.
Combining this with (7), which we rewrite using (9), we obtain
as above, and again equality holds all along. In particular,
![]() $$b_r(G) = b_{1/r}^\bullet (G^*)^r = (b_{1/r}^*(G))^r.$$
$$b_r(G) = b_{1/r}^\bullet (G^*)^r = (b_{1/r}^*(G))^r.$$
If
![]() $b_r$
or
$b_r$
or
![]() $b_{1/r}$
is equal to
$b_{1/r}$
is equal to
![]() $0$
, then the same argument shows that both
$0$
, then the same argument shows that both
![]() $b_r$
and
$b_r$
and
![]() $b_{1/r}$
are equal to
$b_{1/r}$
are equal to
![]() $0$
. This completes the proof.
$0$
. This completes the proof.
The arguments in the proofs of Proposition 5.3 and Theorem 5.6 can be used to prove Lemma 4.2.
Proof of Lemma 4.2. The inequality
![]() $b_r^\circ \leq b_r^\odot$
is obvious.
$b_r^\circ \leq b_r^\odot$
is obvious.
For the reverse inequality, we will focus on the case of site interfaces. We will construct an array of a certain number of boxes of possibly different sizes, then place the component site interfaces of an arbitrary site multi-interface inside the boxes, and connect them with short paths to obtain a new site interface.
We claim that the number of choices for the shapes of the components of any site multi-interface of size
![]() $n$
grows subexponentially in
$n$
grows subexponentially in
![]() $n$
. Indeed, the number of choices for the shape of any site interface grows polynomially in its size. Theorem 2.1 shows that there are most
$n$
. Indeed, the number of choices for the shape of any site interface grows polynomially in its size. Theorem 2.1 shows that there are most
![]() $s^{\sqrt{n}}$
choices for the component sizes of any site multi-interface of size
$s^{\sqrt{n}}$
choices for the component sizes of any site multi-interface of size
![]() $n$
, where
$n$
, where
![]() $s\gt 0$
is a constant. Hence it suffices to show that a site multi-interface of size
$s\gt 0$
is a constant. Hence it suffices to show that a site multi-interface of size
![]() $n$
comprises
$n$
comprises
![]() $O(\sqrt{n})$
site interfaces.
$O(\sqrt{n})$
site interfaces.
Let
![]() $X=(\ldots,x_{-1},x_0=o,x_1,\ldots )$
be a quasi-geodesic in
$X=(\ldots,x_{-1},x_0=o,x_1,\ldots )$
be a quasi-geodesic in
![]() $G$
containing
$G$
containing
![]() $o$
and let
$o$
and let
![]() $X^+=(x_0,x_1,\ldots )$
be the one of the two
$X^+=(x_0,x_1,\ldots )$
be the one of the two
![]() $1$
-way infinite subpaths of
$1$
-way infinite subpaths of
![]() $X$
starting from
$X$
starting from
![]() $o$
. Consider a site multi-interface
$o$
. Consider a site multi-interface
![]() $P$
of size
$P$
of size
![]() $n$
. As remarked in the proof of Proposition 4.4,
$n$
. As remarked in the proof of Proposition 4.4,
![]() $P$
contains at least one of the first
$P$
contains at least one of the first
![]() $ln+1$
vertices of
$ln+1$
vertices of
![]() $X^+$
. We enumerate the component site interfaces
$X^+$
. We enumerate the component site interfaces
![]() $P_1,P_2,\ldots,P_k$
of
$P_1,P_2,\ldots,P_k$
of
![]() $P$
according to the first vertex of
$P$
according to the first vertex of
![]() $X^+$
that they contain. As the
$X^+$
that they contain. As the
![]() $P_i$
’s are disjoint, we have
$P_i$
’s are disjoint, we have
![]() $l_i\lt l_{i+1}$
, where
$l_i\lt l_{i+1}$
, where
![]() $l_i$
is the index of the first vertex of
$l_i$
is the index of the first vertex of
![]() $X^+$
that
$X^+$
that
![]() $P_i$
contains. Since
$P_i$
contains. Since
![]() $l_1\geq 0$
, we deduce that
$l_1\geq 0$
, we deduce that
![]() $l_i\geq i-1$
for every
$l_i\geq i-1$
for every
![]() $i$
. Hence, we obtain
$i$
. Hence, we obtain
for every
![]() $i=1,2,\ldots,k$
, which implies that
$i=1,2,\ldots,k$
, which implies that
 \begin{equation*}n=\sum _{i=1}^k |P_i|\geq \sum _{i=1}^k (i-1)/l=\frac {k(k-1)}{2l}.\end{equation*}
\begin{equation*}n=\sum _{i=1}^k |P_i|\geq \sum _{i=1}^k (i-1)/l=\frac {k(k-1)}{2l}.\end{equation*}
The latter implies that
![]() $k=O(\sqrt{n})$
, hence there are
$k=O(\sqrt{n})$
, hence there are
![]() $(sn)^{O(\sqrt{n})}$
choices for the shapes of the components site interfaces of any site multi-interface of size
$(sn)^{O(\sqrt{n})}$
choices for the shapes of the components site interfaces of any site multi-interface of size
![]() $n$
.
$n$
.
We can now restrict to a subfamily
![]() $K\subset MI_{n,r,\epsilon }$
of size at least
$K\subset MI_{n,r,\epsilon }$
of size at least
such that all site multi-interfaces of
![]() $K$
have the same component sizes, say
$K$
have the same component sizes, say
![]() $\{n_1,n_2,\ldots,n_k\}$
, and corresponding component site interfaces have the same shape. Let
$\{n_1,n_2,\ldots,n_k\}$
, and corresponding component site interfaces have the same shape. Let
![]() $B_1,B_2,\ldots,B_k$
be the boxes of the component site interfaces. Instead of a grid, we construct an array by placing the above
$B_1,B_2,\ldots,B_k$
be the boxes of the component site interfaces. Instead of a grid, we construct an array by placing the above
![]() $k$
boxes next to each other. Given an element of
$k$
boxes next to each other. Given an element of
![]() $K$
, we place its component site interfaces in their boxes. After moving the boxes, if necessary, we connect them with short paths, as described in the proof of Lemma 5.6. Arguing as in the proof of Lemma 5.6 we obtain
$K$
, we place its component site interfaces in their boxes. After moving the boxes, if necessary, we connect them with short paths, as described in the proof of Lemma 5.6. Arguing as in the proof of Lemma 5.6 we obtain
![]() $b_r^\circ \geq b_r^\odot$
, as desired.
$b_r^\circ \geq b_r^\odot$
, as desired.
Since
![]() ${\mathbb{P}}_{p_c}(|S_o|=n)$
does not decay exponentially in
${\mathbb{P}}_{p_c}(|S_o|=n)$
does not decay exponentially in
![]() $n$
, we conclude
$n$
, we conclude
Corollary 5.7.
Consider site percolation on a graph
![]() $G\in \mathcal{S}$
satisfying (4). Then,
$G\in \mathcal{S}$
satisfying (4). Then,
![]() ${\mathbb{P}}_{1-p_c}(|S_o|=n)$
does not decay exponentially in
${\mathbb{P}}_{1-p_c}(|S_o|=n)$
does not decay exponentially in
![]() $n$
.
$n$
.
Proof. Notice that
![]() $r(1-p_c)=1/r(p_c)$
. The fact that
$r(1-p_c)=1/r(p_c)$
. The fact that
![]() ${\mathbb{P}}_{p_c}(|S_o|=n)$
does not decay exponentially in
${\mathbb{P}}_{p_c}(|S_o|=n)$
does not decay exponentially in
![]() $n$
implies that
$n$
implies that
![]() $b_{r(p_c)}=f(r(p_c))$
. Theorem 5.1 shows that
$b_{r(p_c)}=f(r(p_c))$
. Theorem 5.1 shows that
Using Theorem 1.2 we conclude that
![]() ${\mathbb{P}}_{1-p_c}(|S_o|=n)$
does not decay exponentially in
${\mathbb{P}}_{1-p_c}(|S_o|=n)$
does not decay exponentially in
![]() $n$
.
$n$
.
6. Continuity
In this section, we study the analytical properties of
![]() $b_r$
. To avoid repeating the arguments in the proof of Lemma 5.6 and considering cases according to whether we study interfaces or site interfaces, we will prove the results for interfaces in
$b_r$
. To avoid repeating the arguments in the proof of Lemma 5.6 and considering cases according to whether we study interfaces or site interfaces, we will prove the results for interfaces in
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
, where the latter graph is defined in (c).
$\mathbb{T}^d$
, where the latter graph is defined in (c).
We first prove that the
![]() $\limsup$
in the definition of
$\limsup$
in the definition of
![]() $b_r$
can be replaced by
$b_r$
can be replaced by
![]() $\lim$
.
$\lim$
.
Proposition 6.1.
Let
![]() $G\in \mathcal{S}$
. Then, for every
$G\in \mathcal{S}$
. Then, for every
![]() $r$
such that
$r$
such that
![]() $b_r\gt 1$
and for all but countably many
$b_r\gt 1$
and for all but countably many
![]() $\epsilon \gt 0$
the limit
$\epsilon \gt 0$
the limit
![]() $\lim _{n\to \infty } c_{n,r,\epsilon }(G)^{1/n}$
exists.
$\lim _{n\to \infty } c_{n,r,\epsilon }(G)^{1/n}$
exists.
Proof. We will first show that
holds for any
![]() $\epsilon \gt 0$
at which the function
$\epsilon \gt 0$
at which the function
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
is continuous. Since
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
is continuous. Since
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
is an increasing function of
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
is an increasing function of
![]() $\epsilon$
, its points of discontinuity are countably many [Reference Rudin41].
$\epsilon$
, its points of discontinuity are countably many [Reference Rudin41].
Let
![]() $\epsilon$
be a point of continuity of
$\epsilon$
be a point of continuity of
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
![]() $n\in{\mathbb N}$
. By combining elements of
$n\in{\mathbb N}$
. By combining elements of
![]() $I_{n,r,\epsilon }$
we will construct interfaces of arbitrarily large size and surface-to-volume ratio between
$I_{n,r,\epsilon }$
we will construct interfaces of arbitrarily large size and surface-to-volume ratio between
![]() $r-\epsilon ^{\prime}$
and
$r-\epsilon ^{\prime}$
and
![]() $r+\epsilon ^{\prime}$
for some
$r+\epsilon ^{\prime}$
for some
![]() $\epsilon \leq \epsilon ^{\prime}=\epsilon +o(1)$
. Let
$\epsilon \leq \epsilon ^{\prime}=\epsilon +o(1)$
. Let
![]() $0\leq s\leq n+3$
be an integer. We repeat the idea of Proposition 5.3, but instead of a grid, we construct an array of
$0\leq s\leq n+3$
be an integer. We repeat the idea of Proposition 5.3, but instead of a grid, we construct an array of
![]() $m$
boxes for some
$m$
boxes for some
![]() $m\gt 0$
. We place inside each box an element of
$m\gt 0$
. We place inside each box an element of
![]() $I_{n,r,\epsilon }$
and after moving the boxes, if necessary, we connect consecutive interfaces using paths of length
$I_{n,r,\epsilon }$
and after moving the boxes, if necessary, we connect consecutive interfaces using paths of length
![]() $4$
, similarly to the proof of Proposition 5.3. We also attach a path of length
$4$
, similarly to the proof of Proposition 5.3. We also attach a path of length
![]() $s+4$
, that is incident to the last interface and disjoint from any of the previous interfaces. In this way, we produce an element
$s+4$
, that is incident to the last interface and disjoint from any of the previous interfaces. In this way, we produce an element
![]() $Q$
of
$Q$
of
![]() $I_{k,r,\epsilon ^{\prime}}$
, where
$I_{k,r,\epsilon ^{\prime}}$
, where
![]() $\epsilon ^{\prime}=\epsilon +o(1)$
and
$\epsilon ^{\prime}=\epsilon +o(1)$
and
![]() $k$
is any integer of the form
$k$
is any integer of the form
![]() $k=m(n+4)+s$
. There are roughly
$k=m(n+4)+s$
. There are roughly
![]() $c_{n,r,\epsilon }^m$
choices for
$c_{n,r,\epsilon }^m$
choices for
![]() $Q$
. Since
$Q$
. Since
![]() $s$
ranges between
$s$
ranges between
![]() $0$
and
$0$
and
![]() $n+3$
, for every fixed
$n+3$
, for every fixed
![]() $n$
, all but finitely many
$n$
, all but finitely many
![]() $k$
can be written in this form for some
$k$
can be written in this form for some
![]() $m\geq 1$
. Taking the
$m\geq 1$
. Taking the
![]() $k$
th root and then the limit as
$k$
th root and then the limit as
![]() $m\to \infty$
we conclude that
$m\to \infty$
we conclude that
![]() $\liminf _{k\to \infty } c_{k,r,\epsilon ^{\prime}}^{1/k}\geq c_{n,r,\epsilon }^{1/(n+4)}$
. Letting
$\liminf _{k\to \infty } c_{k,r,\epsilon ^{\prime}}^{1/k}\geq c_{n,r,\epsilon }^{1/(n+4)}$
. Letting
![]() $n\to \infty$
we obtain
$n\to \infty$
we obtain
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n} \geq \limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
. The above inequality follows from the fact that
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n} \geq \limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
. The above inequality follows from the fact that
![]() $\epsilon$
is a point of continuity of
$\epsilon$
is a point of continuity of
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
. Hence
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
. Hence
![]() $\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n} = \limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
, as desired
$\liminf _{n\to \infty } c_{n,r,\epsilon }^{1/n} = \limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
, as desired
The following proposition follows directly from the definition of
![]() $b_r$
:
$b_r$
:
Proposition 6.2.
Let
![]() $G\in \mathcal{S}$
. Then
$G\in \mathcal{S}$
. Then
![]() $b_r(G)$
is an upper-semicontinuous function of
$b_r(G)$
is an upper-semicontinuous function of
![]() $r$
.
$r$
.
Proof. Let
![]() $\epsilon \gt 0$
and
$\epsilon \gt 0$
and
![]() $0\lt \delta \lt \epsilon/2$
. Then for every
$0\lt \delta \lt \epsilon/2$
. Then for every
![]() $r\gt 0$
and for every
$r\gt 0$
and for every
![]() $s$
with
$s$
with
![]() $|r-s|\lt \epsilon/2$
, the interval
$|r-s|\lt \epsilon/2$
, the interval
![]() $(s-\delta,s+\delta )$
is contained in
$(s-\delta,s+\delta )$
is contained in
![]() $(r-\epsilon,r+\epsilon )$
, and the site interfaces
$(r-\epsilon,r+\epsilon )$
, and the site interfaces
![]() $P$
with
$P$
with
![]() $|\partial P|/|P| \in (s-\delta,s+\delta )$
are counted in the set of those site interfaces with
$|\partial P|/|P| \in (s-\delta,s+\delta )$
are counted in the set of those site interfaces with
![]() $|\partial P|/|P| \in (r-\epsilon,r+\epsilon )$
as well. Hence,
$|\partial P|/|P| \in (r-\epsilon,r+\epsilon )$
as well. Hence,
![]() $\limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}\geq \limsup _{n\to \infty } c_{n,s,\delta }^{1/n}$
. Taking limits as
$\limsup _{n\to \infty } c_{n,r,\epsilon }^{1/n}\geq \limsup _{n\to \infty } c_{n,s,\delta }^{1/n}$
. Taking limits as
![]() $\delta \to 0$
,
$\delta \to 0$
,
![]() $s\to r$
and finally
$s\to r$
and finally
![]() $\epsilon \to 0$
, we obtain
$\epsilon \to 0$
, we obtain
![]() $b_r \geq \limsup _{s\to r} b_s$
. The latter shows that
$b_r \geq \limsup _{s\to r} b_s$
. The latter shows that
![]() $b_r$
is an upper-semicontinuous function of
$b_r$
is an upper-semicontinuous function of
![]() $r$
.
$r$
.
Next, we prove that
![]() $b_r$
is a log-concave function of
$b_r$
is a log-concave function of
![]() $r$
.
$r$
.
Proposition 6.3.
Let
![]() $G\in \mathcal{S}$
. Then for any
$G\in \mathcal{S}$
. Then for any
![]() $t\in (0,1)$
and any
$t\in (0,1)$
and any
![]() $r,s$
such that
$r,s$
such that
![]() $b_r(G),b_s(G)\gt 1$
, we have
$b_r(G),b_s(G)\gt 1$
, we have
![]() $b_{tr+(1-t)s}(G) \geq b_r(G)^{t} b_s(G)^{1-t}$
.
$b_{tr+(1-t)s}(G) \geq b_r(G)^{t} b_s(G)^{1-t}$
.
Proof. Pick an
![]() $\epsilon \gt 0$
such that both
$\epsilon \gt 0$
such that both
![]() $\lim _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
$\lim _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
![]() $\lim _{n\to \infty } c_{n,s,\epsilon }^{1/n}$
exist. Let
$\lim _{n\to \infty } c_{n,s,\epsilon }^{1/n}$
exist. Let
![]() $(p_m/q_m)$
be a sequence of rational numbers converging to
$(p_m/q_m)$
be a sequence of rational numbers converging to
![]() $t$
such that
$t$
such that
![]() $p_m\to \infty$
and
$p_m\to \infty$
and
![]() $q_m\to \infty$
. Our aim is to construct an interface
$q_m\to \infty$
. Our aim is to construct an interface
![]() $(Q,\partial Q)$
with
$(Q,\partial Q)$
with
![]() $Q$
of size roughly
$Q$
of size roughly
![]() $q_m$
and
$q_m$
and
![]() $\partial Q$
of size roughly
$\partial Q$
of size roughly
![]() $rp_m+s(q_m-p_m)$
, in which case the surface-to-volume ratio is roughly
$rp_m+s(q_m-p_m)$
, in which case the surface-to-volume ratio is roughly
![]() $tr+(1-t)s$
.
$tr+(1-t)s$
.
To this end, consider
![]() $m$
large enough so that
$m$
large enough so that
![]() $q_m\gt p_m$
. Note that there exist subfamilies
$q_m\gt p_m$
. Note that there exist subfamilies
![]() $K$
,
$K$
,
![]() $K^{\prime}$
of
$K^{\prime}$
of
![]() $I_{p_m,r,\epsilon }$
and
$I_{p_m,r,\epsilon }$
and
![]() $I_{q_m-p_m,s,\epsilon }$
and a polynomial
$I_{q_m-p_m,s,\epsilon }$
and a polynomial
![]() $P(x)$
such that the elements of both
$P(x)$
such that the elements of both
![]() $K$
and
$K$
and
![]() $K^{\prime}$
have the same shape (as defined in the proof of Proposition 5.3), and
$K^{\prime}$
have the same shape (as defined in the proof of Proposition 5.3), and
![]() $|K|\geq c_{p_m,r,\epsilon }/P(p_m)$
,
$|K|\geq c_{p_m,r,\epsilon }/P(p_m)$
,
![]() $|K^{\prime}|\geq c_{q_m-p_m,s,\epsilon }/P(q_m-p_m)$
. Note that the elements of
$|K^{\prime}|\geq c_{q_m-p_m,s,\epsilon }/P(q_m-p_m)$
. Note that the elements of
![]() $K$
and
$K$
and
![]() $K^{\prime}$
share the same boxes
$K^{\prime}$
share the same boxes
![]() $B$
and
$B$
and
![]() $B^{\prime}$
, respectively. Consider an interface chosen from
$B^{\prime}$
, respectively. Consider an interface chosen from
![]() $K$
and another interface chosen from
$K$
and another interface chosen from
![]() $K^{\prime}$
, and place them in an array of two boxes
$K^{\prime}$
, and place them in an array of two boxes
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, where
$B_2$
, where
![]() $B_1$
has the same dimensions as
$B_1$
has the same dimensions as
![]() $B$
and
$B$
and
![]() $B_2$
has the same dimensions as
$B_2$
has the same dimensions as
![]() $B^{\prime}$
. Moving
$B^{\prime}$
. Moving
![]() $B_1$
and
$B_1$
and
![]() $B_2$
as appropriate, we can connect the interfaces with paths of length
$B_2$
as appropriate, we can connect the interfaces with paths of length
![]() $O(1)$
.
$O(1)$
.
In this way, we obtain an interface
![]() $Q$
of size
$Q$
of size
![]() $k=q_m+O(1)$
and surface-to-volume ratio
$k=q_m+O(1)$
and surface-to-volume ratio
which converges to
![]() $tr+(1-t)s$
as
$tr+(1-t)s$
as
![]() $m$
tends to infinity and
$m$
tends to infinity and
![]() $\varepsilon$
to
$\varepsilon$
to
![]() $0$
. Notice that we have at least
$0$
. Notice that we have at least
choices for
![]() $Q$
. Taking the
$Q$
. Taking the
![]() $k$
th root of the latter expression and letting
$k$
th root of the latter expression and letting
![]() $m\to \infty$
gives
$m\to \infty$
gives
Letting
![]() $\epsilon \to 0$
along a sequence of points such that both
$\epsilon \to 0$
along a sequence of points such that both
![]() $\lim _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
$\lim _{n\to \infty } c_{n,r,\epsilon }^{1/n}$
and
![]() $\lim _{n\to \infty } c_{n,s,\epsilon }^{1/n}$
exist, we obtain
$\lim _{n\to \infty } c_{n,s,\epsilon }^{1/n}$
exist, we obtain
![]() $b_{tr+(1-t)s} \geq b_r^t b_s^{1-t}$
as desired.
$b_{tr+(1-t)s} \geq b_r^t b_s^{1-t}$
as desired.
We expect Proposition 6.3, and as a result Theorem 6.4 below, to hold in much greater generality than
![]() $G\in \mathcal{S}$
, namely for all 1-ended Cayley graph s. In order to be able to put several interfaces close to each other to connect them with short paths as in the above proof, it could be handy to use [Reference Bandyopadhyay, Steif and Timár3, Lemma 6].
$G\in \mathcal{S}$
, namely for all 1-ended Cayley graph s. In order to be able to put several interfaces close to each other to connect them with short paths as in the above proof, it could be handy to use [Reference Bandyopadhyay, Steif and Timár3, Lemma 6].
Let
![]() $I$
be the closure of the set of
$I$
be the closure of the set of
![]() $r$
such that
$r$
such that
![]() $b_r\gt 1$
. Proposition 6.3, combined with Proposition 6.2, easily implies the following.
$b_r\gt 1$
. Proposition 6.3, combined with Proposition 6.2, easily implies the following.
Theorem 6.4.
Let
![]() $G\in \mathcal{S}$
. Then
$G\in \mathcal{S}$
. Then
![]() $b_r(G)$
is a continuous function of
$b_r(G)$
is a continuous function of
![]() $r$
on
$r$
on
![]() $I$
.
$I$
.
Proof. By Proposition 6.3,
![]() $I$
is an interval, and the only possible
$I$
is an interval, and the only possible
![]() $r\in I$
such that
$r\in I$
such that
![]() $b_r=1$
, are its endpoints. For every
$b_r=1$
, are its endpoints. For every
![]() $r$
in
$r$
in
![]() $I$
, we have
$I$
, we have
![]() $\limsup _{s \to r} b_s \leq b_r$
by Proposition 6.2. Using Proposition 6.3 for
$\limsup _{s \to r} b_s \leq b_r$
by Proposition 6.2. Using Proposition 6.3 for
![]() $t=1/2$
we obtain
$t=1/2$
we obtain
![]() $\liminf _{s\to r} b_{(r+s)/2} \geq \sqrt{b_r \liminf _{s \to r} b_s}$
for every
$\liminf _{s\to r} b_{(r+s)/2} \geq \sqrt{b_r \liminf _{s \to r} b_s}$
for every
![]() $r$
such that
$r$
such that
![]() $b_r\gt 1$
. This immediately implies that
$b_r\gt 1$
. This immediately implies that
![]() $\liminf _{s\to r} b_s\geq b_r$
and thus
$\liminf _{s\to r} b_s\geq b_r$
and thus
![]() $\lim _{s\to r} b_s = b_r$
.
$\lim _{s\to r} b_s = b_r$
.
On the other hand, if
![]() $b_r=1$
for some of the endpoints of
$b_r=1$
for some of the endpoints of
![]() $I$
, then Proposition 6.2 and the fact that
$I$
, then Proposition 6.2 and the fact that
![]() $b_s\gt 1$
for
$b_s\gt 1$
for
![]() $s$
in the interior of
$s$
in the interior of
![]() $I$
, give that
$I$
, give that
Therefore,
![]() $b_r$
is a continuous function on
$b_r$
is a continuous function on
![]() $I$
.
$I$
.
Having proved that
![]() $b_r$
is a continuous function, the next natural question is whether it is differentiable. It turns out that this holds everywhere except, perhaps, on a countable set.
$b_r$
is a continuous function, the next natural question is whether it is differentiable. It turns out that this holds everywhere except, perhaps, on a countable set.
Corollary 6.5.
Let
![]() $G\in \mathcal{S}$
. Then
$G\in \mathcal{S}$
. Then
![]() $b_r(G)$
is differentiable for all but countably many
$b_r(G)$
is differentiable for all but countably many
![]() $r$
.
$r$
.
Proof. By Proposition 6.3,
![]() $\log b_r$
is a concave function, hence differentiable everywhere except for a countable set [Reference Rockafellar40]. It follows immediately that this holds for
$\log b_r$
is a concave function, hence differentiable everywhere except for a countable set [Reference Rockafellar40]. It follows immediately that this holds for
![]() $b_r$
as well.
$b_r$
as well.
7. Bounds on growth rates of lattice animals and interfaces
In this section, we exploit the machinery developed above in order to obtain bounds on the exponential growth rates of lattice (site) animals in
![]() ${\mathbb{Z}}^d$
.
${\mathbb{Z}}^d$
.
A lattice animal in a graph
![]() $G$
is a connected subgraph of
$G$
is a connected subgraph of
![]() $G$
containing
$G$
containing
![]() $o$
. A lattice tree in
$o$
. A lattice tree in
![]() $G$
is a lattice animal that is also a tree. Let
$G$
is a lattice animal that is also a tree. Let
![]() $a_n(G)$
be the number of all lattice animals of
$a_n(G)$
be the number of all lattice animals of
![]() $G$
with
$G$
with
![]() $n$
edges, and let
$n$
edges, and let
![]() $t_n(G)$
be the number of all lattice trees of
$t_n(G)$
be the number of all lattice trees of
![]() $G$
with
$G$
with
![]() $n$
edges. It is well known that both
$n$
edges. It is well known that both
![]() $a({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{a_n({\mathbb{Z}}^d)}^{1/n}$
and
$a({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{a_n({\mathbb{Z}}^d)}^{1/n}$
and
![]() $t({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{t_n({\mathbb{Z}}^d)}^{1/n}$
exist [Reference Klarner30, Reference Klein32].
$t({\mathbb{Z}}^d)\,:\!=\lim _{n\to \infty }{t_n({\mathbb{Z}}^d)}^{1/n}$
exist [Reference Klarner30, Reference Klein32].
A lattice site animal in
![]() $G$
is a set of vertices of
$G$
is a set of vertices of
![]() $G$
containing
$G$
containing
![]() $o$
that spans a connected graph. A lattice site tree in
$o$
that spans a connected graph. A lattice site tree in
![]() $G$
is a lattice site animal in
$G$
is a lattice site animal in
![]() $G$
that spans a tree. Let
$G$
that spans a tree. Let
![]() $\dot{a}_n(G)$
be the number of all lattice site animals of
$\dot{a}_n(G)$
be the number of all lattice site animals of
![]() $G$
with
$G$
with
![]() $n$
vertices, and let
$n$
vertices, and let
![]() $\dot{t}_n(G)$
be the number of all lattice trees of
$\dot{t}_n(G)$
be the number of all lattice trees of
![]() $G$
with
$G$
with
![]() $n$
vertices. We let
$n$
vertices. We let
![]() $\dot{a}(G)\,:\!=\lim _{n\to \infty }{\dot{a}_n(G)}^{1/n}$
and
$\dot{a}(G)\,:\!=\lim _{n\to \infty }{\dot{a}_n(G)}^{1/n}$
and
![]() $\dot{t}(G)\,:\!=\lim _{n\to \infty }{\dot{t}_n(G)}^{1/n}$
whenever the limits exist. It is well known that both limits exist in the case of
$\dot{t}(G)\,:\!=\lim _{n\to \infty }{\dot{t}_n(G)}^{1/n}$
whenever the limits exist. It is well known that both limits exist in the case of
![]() ${\mathbb{Z}}^d$
.
${\mathbb{Z}}^d$
.
Our results allow us to translate any upper bound on
![]() $\dot{p}_c(G)$
into a lower bound on
$\dot{p}_c(G)$
into a lower bound on
![]() $\dot{a}(G)$
, and conversely any upper bound on
$\dot{a}(G)$
, and conversely any upper bound on
![]() $\dot{a}(G)$
into a lower bound on
$\dot{a}(G)$
into a lower bound on
![]() $\dot{p}_c(G)$
. Indeed, we just remark that
$\dot{p}_c(G)$
. Indeed, we just remark that
for every lattice
![]() $G$
, where the two inequalities are obvious from the definitions (interfaces are a species of lattice animal), and the last equality is given by Theorem 4.8. To translate bounds on
$G$
, where the two inequalities are obvious from the definitions (interfaces are a species of lattice animal), and the last equality is given by Theorem 4.8. To translate bounds on
![]() $\dot{p}_c(G)$
into bounds on
$\dot{p}_c(G)$
into bounds on
![]() $\dot{a}(G)$
and vice versa, we just remark that
$\dot{a}(G)$
and vice versa, we just remark that
![]() $f(r)$
is monotone increasing in
$f(r)$
is monotone increasing in
![]() $r$
and
$r$
and
![]() $r(p)$
is monotone decreasing in
$r(p)$
is monotone decreasing in
![]() $p$
. Inequality (10) and the above reasoning applies verbatim to
$p$
. Inequality (10) and the above reasoning applies verbatim to
![]() $p_c(G)$
and
$p_c(G)$
and
![]() ${a}(G)$
.
${a}(G)$
.
Recently, Barequet and Shalah [Reference Barequet and Shalah6] proved that
![]() $\dot{a}({\mathbb{Z}}^3)\lt 9.3835$
. Plugging this into (10), we deduce
$\dot{a}({\mathbb{Z}}^3)\lt 9.3835$
. Plugging this into (10), we deduce
Theorem 7.1.
We have
![]() $\dot{p}_c({\mathbb{Z}}^3)\gt 0.2522$
.
$\dot{p}_c({\mathbb{Z}}^3)\gt 0.2522$
.
As far as we know, the best rigorous bound previously known was about
![]() $\dot{p}_c({\mathbb{Z}}^3)\gt 0.21225$
, obtained as the inverse of the best known bound on the connective constant [Reference MacDonald, Joseph, Hunter, Moseley, Jan and Guttmann34].Footnote
2
$\dot{p}_c({\mathbb{Z}}^3)\gt 0.21225$
, obtained as the inverse of the best known bound on the connective constant [Reference MacDonald, Joseph, Hunter, Moseley, Jan and Guttmann34].Footnote
2
In two dimensions we cannot hope to get close to the real value of
![]() $\dot{a}(G)$
with this technique, as we are only enumerating the subspecies of site interfaces.Footnote
3
But as we will see in the next section, our lower bounds become asymptotically tight as the dimension
$\dot{a}(G)$
with this technique, as we are only enumerating the subspecies of site interfaces.Footnote
3
But as we will see in the next section, our lower bounds become asymptotically tight as the dimension
![]() $d$
tends to infinity. In Section 8 we will argue conversely: we will prove upper bounds on
$d$
tends to infinity. In Section 8 we will argue conversely: we will prove upper bounds on
![]() $\dot{a}({\mathbb{Z}}^d)$
and plug them into (10) to obtain lower bounds on
$\dot{a}({\mathbb{Z}}^d)$
and plug them into (10) to obtain lower bounds on
![]() $\dot{p}_c({\mathbb{Z}}^d)$
.
$\dot{p}_c({\mathbb{Z}}^d)$
.
7.1. Asymptotic expansions
Our first result provides the first terms of the
![]() $1/d$
asymptotic expansion of the exponential growth rate of interfaces:
$1/d$
asymptotic expansion of the exponential growth rate of interfaces:
Theorem 7.2.
The exponential growth rate of the number of interfaces of
![]() ${\mathbb{Z}}^d$
satisfies
${\mathbb{Z}}^d$
satisfies
![]() $b({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
.
$b({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
.
Proof. We claim that for any interface
![]() $P$
of
$P$
of
![]() ${\mathbb{Z}}^d$
we have
${\mathbb{Z}}^d$
we have
![]() $|\partial P|\leq (2d-2)|P|+2d$
. Indeed, summing vertex degrees gives
$|\partial P|\leq (2d-2)|P|+2d$
. Indeed, summing vertex degrees gives
![]() $\sum _{u\in V(P)} \text{deg}(u)\geq 2|P|+|\partial P|$
, where
$\sum _{u\in V(P)} \text{deg}(u)\geq 2|P|+|\partial P|$
, where
![]() $\text{deg}(u)$
is the degree of
$\text{deg}(u)$
is the degree of
![]() $u$
in the graph
$u$
in the graph
![]() $P\cup \partial P$
, because the edges of
$P\cup \partial P$
, because the edges of
![]() $P$
are counted twice, and the edges of
$P$
are counted twice, and the edges of
![]() $\partial P$
are counted at least once. Since
$\partial P$
are counted at least once. Since
![]() $\text{deg}(u)\leq 2d$
and
$\text{deg}(u)\leq 2d$
and
![]() $|V(P)|\leq |P|+1$
, we get
$|V(P)|\leq |P|+1$
, we get
By rearranging we obtain the desired inequality. It follows that
![]() $b_r=0$
for every
$b_r=0$
for every
![]() $r\gt 2d-2$
which combined with (6) and the fact that
$r\gt 2d-2$
which combined with (6) and the fact that
![]() $f(r)$
is an increasing function of
$f(r)$
is an increasing function of
![]() $r$
gives
$r$
gives
for
![]() $r\geq 0$
. Using (4.3) we obtain that
$r\geq 0$
. Using (4.3) we obtain that
Notice that for every
![]() $r\gt 0$
,
$r\gt 0$
,
Using the Taylor expansion
![]() $\log \Big (1+\dfrac{1}{r}\Big )=\dfrac{1}{r}-\dfrac{1}{2r^2}+\dfrac{1}{3r^3}-O(1/r^4)$
we obtain
$\log \Big (1+\dfrac{1}{r}\Big )=\dfrac{1}{r}-\dfrac{1}{2r^2}+\dfrac{1}{3r^3}-O(1/r^4)$
we obtain
as
![]() $r\to \infty$
. Now the Taylor expansion
$r\to \infty$
. Now the Taylor expansion
where
![]() $x=-\dfrac{1}{2r}+\dfrac{1}{3r^2}-O(1/r^3)$
, gives
$x=-\dfrac{1}{2r}+\dfrac{1}{3r^2}-O(1/r^3)$
, gives
 \begin{align*} (1+r)\exp \Big (1-\dfrac{1}{2r}+\dfrac{1}{3r^2}-O(1/r^3)\Big )&=(1+r)e\Big (1-\dfrac{1}{2r}+\dfrac{11}{24r^2}-O(1/r^3)\Big )\\ & = er+\dfrac{e}{2}-O(1/r). \end{align*}
\begin{align*} (1+r)\exp \Big (1-\dfrac{1}{2r}+\dfrac{1}{3r^2}-O(1/r^3)\Big )&=(1+r)e\Big (1-\dfrac{1}{2r}+\dfrac{11}{24r^2}-O(1/r^3)\Big )\\ & = er+\dfrac{e}{2}-O(1/r). \end{align*}
Consequently,
Plugging
![]() $r=2d-2$
in (13) we deduce that
$r=2d-2$
in (13) we deduce that
which combined with (12) establishes the desired upper bound.
For the lower bound, we have
![]() $b({\mathbb{Z}}^d)\geq b_{r_d}({\mathbb{Z}}^d)$
and
$b({\mathbb{Z}}^d)\geq b_{r_d}({\mathbb{Z}}^d)$
and
![]() $b_{r_d}({\mathbb{Z}}^d)=f(r_d)$
, where
$b_{r_d}({\mathbb{Z}}^d)=f(r_d)$
, where
![]() $r_d\,:\!=r(p_c({\mathbb{Z}}^d))$
. It has been proved in [Reference Hara and Slade20, Reference Van Der Hofstad and Slade26] that
$r_d\,:\!=r(p_c({\mathbb{Z}}^d))$
. It has been proved in [Reference Hara and Slade20, Reference Van Der Hofstad and Slade26] that
hence
We can easily compute that
 \begin{align*} \dfrac{16d^4}{8d^3+4d^2+7d+O(1)}&= 2d-\dfrac{8d^3+14d^2+O(d)}{8d^3+4d^2+7d+O(1)}\\ & = 2d-\dfrac{8d^3+4d^2}{8d^3+4d^2+7d+O(1)}-O(1/d) \end{align*}
\begin{align*} \dfrac{16d^4}{8d^3+4d^2+7d+O(1)}&= 2d-\dfrac{8d^3+14d^2+O(d)}{8d^3+4d^2+7d+O(1)}\\ & = 2d-\dfrac{8d^3+4d^2}{8d^3+4d^2+7d+O(1)}-O(1/d) \end{align*}
and
Hence
![]() $r_d=2d-2-O(1/d)$
, which implies that
$r_d=2d-2-O(1/d)$
, which implies that
Therefore,
![]() $b({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
as desired.
$b({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
as desired.
We remark that the asymptotic expansions of
![]() $\dfrac{(2d-1)^{(2d-1)}}{(2d-2)^{(2d-2)}}$
and
$\dfrac{(2d-1)^{(2d-1)}}{(2d-2)^{(2d-2)}}$
and
![]() $b_{r_d}$
differ in their third terms, and so we are unable to compute the third term in the asymptotic expansion of
$b_{r_d}$
differ in their third terms, and so we are unable to compute the third term in the asymptotic expansion of
![]() $b({\mathbb{Z}}^d)$
. It follows from the proof of Theorem 7.2 above that
$b({\mathbb{Z}}^d)$
. It follows from the proof of Theorem 7.2 above that
![]() $b({\mathbb{Z}}^d)-b_{r_d}({\mathbb{Z}}^d)=O(1/d)$
, that is
$b({\mathbb{Z}}^d)-b_{r_d}({\mathbb{Z}}^d)=O(1/d)$
, that is
![]() $b_{r_d}$
is a good approximation of
$b_{r_d}$
is a good approximation of
![]() $b({\mathbb{Z}}^d)$
.
$b({\mathbb{Z}}^d)$
.
Next, we use Theorem 7.2 and Kesten’s argument [Reference Grimmett18] to obtain the first two terms in the asymptotic expansion of
![]() $a({\mathbb{Z}}^d)$
. These had already been obtained by Miranda and Slade [Reference Miranda and Slade37] but our proof is shorter.
$a({\mathbb{Z}}^d)$
. These had already been obtained by Miranda and Slade [Reference Miranda and Slade37] but our proof is shorter.
Theorem 7.3.
![]() $a({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
.
$a({\mathbb{Z}}^d)=2de-\dfrac{3e}{2}-O(1/d)$
.
Proof. Let
![]() $C$
be a connected subgraph containing
$C$
be a connected subgraph containing
![]() $o$
and recall the definition of the edge boundary
$o$
and recall the definition of the edge boundary
![]() $\partial _E C$
. Arguing as in the proof of Theorem 7.2, we obtain that
$\partial _E C$
. Arguing as in the proof of Theorem 7.2, we obtain that
![]() $|\partial _E C|\leq (2d-2)|E(C)|+2d$
. It follows that for every
$|\partial _E C|\leq (2d-2)|E(C)|+2d$
. It follows that for every
![]() $p\in (0,1)$
.
$p\in (0,1)$
.
Choosing
![]() $p=\frac{1}{2d-1}$
and dividing by
$p=\frac{1}{2d-1}$
and dividing by
![]() $p^n (1-p)^{(2d-2)n+2d}$
, we deduce from (14) that
$p^n (1-p)^{(2d-2)n+2d}$
, we deduce from (14) that
Since
![]() $a({\mathbb{Z}}^d)\geq b({\mathbb{Z}}^d)$
, the lower bound follows from Theorem 7.2.
$a({\mathbb{Z}}^d)\geq b({\mathbb{Z}}^d)$
, the lower bound follows from Theorem 7.2.
The behaviour of
![]() $a({\mathbb{Z}}^d)$
, and the analogue
$a({\mathbb{Z}}^d)$
, and the analogue
![]() $t({\mathbb{Z}}^d)$
for lattice trees, has been extensively studied in the physics literature. Precise asymptotic expansions for
$t({\mathbb{Z}}^d)$
for lattice trees, has been extensively studied in the physics literature. Precise asymptotic expansions for
![]() $a({\mathbb{Z}}^d)$
and
$a({\mathbb{Z}}^d)$
and
![]() $t({\mathbb{Z}}^d)$
were reported in [Reference Gaunt and Peard15], [Reference Harris22, Reference Peard and Gaunt38], respectively, but without any rigorous bounds on the error terms. Miranda and Slade [Reference Miranda and Slade36] proved that both
$t({\mathbb{Z}}^d)$
were reported in [Reference Gaunt and Peard15], [Reference Harris22, Reference Peard and Gaunt38], respectively, but without any rigorous bounds on the error terms. Miranda and Slade [Reference Miranda and Slade36] proved that both
![]() $a({\mathbb{Z}}^d)$
and
$a({\mathbb{Z}}^d)$
and
![]() $t({\mathbb{Z}}^d)$
are asymptotic to
$t({\mathbb{Z}}^d)$
are asymptotic to
![]() $2de$
. The first three terms of
$2de$
. The first three terms of
![]() $a({\mathbb{Z}}^d)$
and
$a({\mathbb{Z}}^d)$
and
![]() $t({\mathbb{Z}}^d)$
have been computed rigorously by the same authors in [Reference Miranda and Slade37].
$t({\mathbb{Z}}^d)$
have been computed rigorously by the same authors in [Reference Miranda and Slade37].
7.2. Site variants
We now prove analogous results for site interfaces and site animals. We start with a weaker analogue of Theorem 7.2:
Theorem 7.4.
The exponential growth rate of the number of site interfaces of
![]() ${\mathbb{Z}}^d$
satisfies
${\mathbb{Z}}^d$
satisfies
![]() $\dot{b}({\mathbb{Z}}^d)=2de-O(1)$
.
$\dot{b}({\mathbb{Z}}^d)=2de-O(1)$
.
Proof. Similarly to the proof of Theorem 7.2, we will show that for any site interface
![]() $P$
of
$P$
of
![]() ${\mathbb{Z}}^d$
we have
${\mathbb{Z}}^d$
we have
![]() $|\partial P|\leq (2d-2)|P|+2$
. Let
$|\partial P|\leq (2d-2)|P|+2$
. Let
![]() $k$
be the number of edges of the graph spanned by
$k$
be the number of edges of the graph spanned by
![]() $P$
, and let
$P$
, and let
![]() $l$
be the number of edges with one end vertex in
$l$
be the number of edges with one end vertex in
![]() $P$
and one in
$P$
and one in
![]() $\partial P$
. Notice that
$\partial P$
. Notice that
![]() $k\geq |P|-1$
and
$k\geq |P|-1$
and
![]() $l\geq |\partial P|$
. Arguing as in the proof of Theorem 7.2 we obtain
$l\geq |\partial P|$
. Arguing as in the proof of Theorem 7.2 we obtain
By rearranging we obtain the desired inequality. Arguing as in the proof of Theorem 7.2 we obtain
Moreover, we have that
![]() $\dot{b}({\mathbb{Z}}^d)\geq \dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)$
and
$\dot{b}({\mathbb{Z}}^d)\geq \dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)$
and
![]() $\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=f(\dot{r}_d)$
, where
$\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=f(\dot{r}_d)$
, where
![]() $\dot{r}_d\,:\!=r({\dot{p}_c}({\mathbb{Z}}^d))$
. Hara and Slade [Reference Hara and Slade20] proved that
$\dot{r}_d\,:\!=r({\dot{p}_c}({\mathbb{Z}}^d))$
. Hara and Slade [Reference Hara and Slade20] proved that
![]() ${\dot{p}_c}({\mathbb{Z}}^d)=\big (1+O(1/d)\big )/2d$
, hence
${\dot{p}_c}({\mathbb{Z}}^d)=\big (1+O(1/d)\big )/2d$
, hence
Using (13) we obtain
 \begin{equation*}\dot {b}_{\dot {r}_d}({\mathbb {Z}}^d)=\frac {(1+\dot {r}_d)^{1+\dot {r}_d}}{\dot {r}_d^{\dot {r}_d}}=\dfrac {2de}{1+O(1/d)}-e/2-O(1/d).\end{equation*}
\begin{equation*}\dot {b}_{\dot {r}_d}({\mathbb {Z}}^d)=\frac {(1+\dot {r}_d)^{1+\dot {r}_d}}{\dot {r}_d^{\dot {r}_d}}=\dfrac {2de}{1+O(1/d)}-e/2-O(1/d).\end{equation*}
Since
![]() $\dfrac{1}{1+O(1/d)}=1-O(1/d)$
, we have
$\dfrac{1}{1+O(1/d)}=1-O(1/d)$
, we have
Therefore,
![]() $\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=2de-O(1)$
, which implies that
$\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=2de-O(1)$
, which implies that
![]() $\dot{b}({\mathbb{Z}}^d)=2de-O(1)$
as desired.
$\dot{b}({\mathbb{Z}}^d)=2de-O(1)$
as desired.
In the previous section we used (10) and (15) to lower bound
![]() $b({\mathbb{Z}}^d)$
. Recently, Heydenreich and Matzke [Reference Heydenreich and Matzke25] proved thatFootnote
4
$b({\mathbb{Z}}^d)$
. Recently, Heydenreich and Matzke [Reference Heydenreich and Matzke25] proved thatFootnote
4
Combining (17) with our above method gives the lower bound
![]() $\dot{a}({\mathbb{Z}}^d)\geq \dot{b}({\mathbb{Z}}^d)\geq 2de-3e+O(1/d)$
. Arguing as in Theorem 7.3, we can easily obtain
$\dot{a}({\mathbb{Z}}^d)\geq \dot{b}({\mathbb{Z}}^d)\geq 2de-3e+O(1/d)$
. Arguing as in Theorem 7.3, we can easily obtain
Theorem 7.5.
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-O(1)$
and
$\dot{a}({\mathbb{Z}}^d)\leq 2de-O(1)$
and
![]() $\dot{a}({\mathbb{Z}}^d)\geq 2de-3e+O(1/d)$
.
$\dot{a}({\mathbb{Z}}^d)\geq 2de-3e+O(1/d)$
.
Barequet, Barequet and Rote [Reference Barequet, Barequet and Rote4] proved the weaker result
![]() $\dot{a}({\mathbb{Z}}^d)=2de-o(d)$
, and they conjectured that
$\dot{a}({\mathbb{Z}}^d)=2de-o(d)$
, and they conjectured that
![]() $\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
in agreement with physicists’ predictions [Reference Peard and Gaunt38, (2.22)], so it only remains to prove a matching upper bound.Footnote
5
We will improve the upper bound in Theorem 8.1 below. We remark that under the assumption
$\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
in agreement with physicists’ predictions [Reference Peard and Gaunt38, (2.22)], so it only remains to prove a matching upper bound.Footnote
5
We will improve the upper bound in Theorem 8.1 below. We remark that under the assumption
![]() $\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
holds, we obtain
$\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
holds, we obtain
![]() $\dot{b}({\mathbb{Z}}^d)-\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=O(1/d)$
.
$\dot{b}({\mathbb{Z}}^d)-\dot{b}_{\dot{r}_d}({\mathbb{Z}}^d)=O(1/d)$
.
8. Upper bounds for lattice site animals
In the previous section, we used Kesten’s argument in order to bound
![]() $\dot{a}({\mathbb{Z}}^d)$
from above. Another method that gives the same upper bounds for
$\dot{a}({\mathbb{Z}}^d)$
from above. Another method that gives the same upper bounds for
![]() $\dot{a}({\mathbb{Z}}^d)$
was introduced by Eden [Reference Eden13]. Eden described a procedure that associates in a canonical way, a spanning tree and a binary sequence to every lattice site animal. This reduces the problem of counting lattice site animals to a problem of counting binary sequences with certain properties. Klarner and Rivest [Reference Klarner and Rivest31] enhanced Eden’s method in the case of
$\dot{a}({\mathbb{Z}}^d)$
was introduced by Eden [Reference Eden13]. Eden described a procedure that associates in a canonical way, a spanning tree and a binary sequence to every lattice site animal. This reduces the problem of counting lattice site animals to a problem of counting binary sequences with certain properties. Klarner and Rivest [Reference Klarner and Rivest31] enhanced Eden’s method in the case of
![]() ${\mathbb{Z}}^2$
, proving that
${\mathbb{Z}}^2$
, proving that
![]() $\dot{a}({\mathbb{Z}}^2)\leq 4.6496$
. Recently, Barequet and Shalah [Reference Barequet and Shalah6] extended this enhancement to higher dimensions, obtaining
$\dot{a}({\mathbb{Z}}^2)\leq 4.6496$
. Recently, Barequet and Shalah [Reference Barequet and Shalah6] extended this enhancement to higher dimensions, obtaining
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
.
$\dot{a}({\mathbb{Z}}^d)\leq 2de-2e+1/(2d-2)$
.
In this section we will utilise Eden’s procedure to reduce the gap between the aforementioned inequality and the conjectured asymptotic expansion
![]() $\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
mentioned in the previous section:
$\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
mentioned in the previous section:
Theorem 8.1.
We have
![]() $\dot{a}({\mathbb{Z}}^d)\leq 2de-5e/2+O(1/\log (d))$
.
$\dot{a}({\mathbb{Z}}^d)\leq 2de-5e/2+O(1/\log (d))$
.
Our result improves the bounds of Barequet and Shalah [Reference Barequet and Shalah6] for every large enough
![]() $d$
.
$d$
.
We remark that
![]() $\dot{b}_{r_d}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
by (17). It is reasonable to expect that both
$\dot{b}_{r_d}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
by (17). It is reasonable to expect that both
![]() $\dot{b}({\mathbb{Z}}^d)-\dot{b}_{r_d}({\mathbb{Z}}^d)=O(1/d)$
and
$\dot{b}({\mathbb{Z}}^d)-\dot{b}_{r_d}({\mathbb{Z}}^d)=O(1/d)$
and
![]() $\dot{a}({\mathbb{Z}}^d) - \dot{b}({\mathbb{Z}}^d)=O(1/d)$
hold, as it happens for the bond variants, which would imply the aforementioned conjecture
$\dot{a}({\mathbb{Z}}^d) - \dot{b}({\mathbb{Z}}^d)=O(1/d)$
hold, as it happens for the bond variants, which would imply the aforementioned conjecture
![]() $\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
.
$\dot{a}({\mathbb{Z}}^d)=2de-3e+O(1/d)$
.
In order to prove Theorem 8.1, we will show that a typical lattice site animal has volume-to-surface ratio that is bounded away from its maximal possible value, namely
![]() $2d-2$
.
$2d-2$
.
We will need the following definition. We let
![]() $\dot{a}_{n,r,\epsilon }$
denote the number of lattice site animals
$\dot{a}_{n,r,\epsilon }$
denote the number of lattice site animals
![]() $X$
of
$X$
of
![]() ${\mathbb{Z}}^d$
containing
${\mathbb{Z}}^d$
containing
![]() $o$
with
$o$
with
![]() $|X|=n$
and
$|X|=n$
and
![]() $(r-\epsilon )n \leq |\partial _V X| \leq (r+\epsilon )n$
, and we define
$(r-\epsilon )n \leq |\partial _V X| \leq (r+\epsilon )n$
, and we define
Using Kesten’s argument, one can show that
for every
![]() $r\gt 0$
. This follows from the work of Hammond [Reference Hammond19], and it can also be seen as a special case of (6), since by choosing the full cycle space of
$r\gt 0$
. This follows from the work of Hammond [Reference Hammond19], and it can also be seen as a special case of (6), since by choosing the full cycle space of
![]() ${\mathbb{Z}}^d$
as its basis, each lattice site animal
${\mathbb{Z}}^d$
as its basis, each lattice site animal
![]() $P$
is a site interface with
$P$
is a site interface with
![]() $\partial P=\partial _V P$
.
$\partial P=\partial _V P$
.
For the proof of Theorem 8.1 we will need a result which bounds
![]() $\dot{a}_r({\mathbb{Z}}^d)$
for
$\dot{a}_r({\mathbb{Z}}^d)$
for
![]() $r$
close to
$r$
close to
![]() $2d-2$
. We remark that
$2d-2$
. We remark that
![]() $\dot{a}_{2d-2}({\mathbb{Z}}^d)\geq \dot{b}_{2d-2}({\mathbb{Z}}^d)\geq 1$
, as a straight path has volume-to-surface ratio roughly
$\dot{a}_{2d-2}({\mathbb{Z}}^d)\geq \dot{b}_{2d-2}({\mathbb{Z}}^d)\geq 1$
, as a straight path has volume-to-surface ratio roughly
![]() $2d-2$
.
$2d-2$
.
Before proving this result, let us first introduce some necessary definitions which will allow us to describe Eden’s procedure. The lexicographical ordering of
![]() ${\mathbb{Z}}^d$
is defined as follows. We say that a vertex
${\mathbb{Z}}^d$
is defined as follows. We say that a vertex
![]() $u=(u_1,u_2,\ldots,u_d)$
is smaller than a vertex
$u=(u_1,u_2,\ldots,u_d)$
is smaller than a vertex
![]() $v=(v_1,v_2,\ldots,v_d)$
if there is some
$v=(v_1,v_2,\ldots,v_d)$
if there is some
![]() $i=1,2,\ldots,d$
such that
$i=1,2,\ldots,d$
such that
![]() $u_i\leq v_i$
and
$u_i\leq v_i$
and
![]() $u_j=v_j$
for every
$u_j=v_j$
for every
![]() $j\lt i$
. We also order the directed edges of the form
$j\lt i$
. We also order the directed edges of the form
![]() $\vec{ou}$
in an arbitrary way. The latter ordering induces by translation a natural ordering of the set of directed edges with a common initial end vertex
$\vec{ou}$
in an arbitrary way. The latter ordering induces by translation a natural ordering of the set of directed edges with a common initial end vertex
![]() $v$
, where
$v$
, where
![]() $v$
is any vertex of
$v$
is any vertex of
![]() ${\mathbb{Z}}^d$
.
${\mathbb{Z}}^d$
.
We will now describe Eden’s procedure. Let
![]() $X$
be a lattice site animal of size
$X$
be a lattice site animal of size
![]() $n$
in
$n$
in
![]() ${\mathbb{Z}}^d$
containing
${\mathbb{Z}}^d$
containing
![]() $o$
. We will assign to
$o$
. We will assign to
![]() $X$
a unique binary sequence
$X$
a unique binary sequence
![]() $S=S(X)=(s_1,s_2,\ldots,s_{(2d-1)n-d+1})$
of length
$S=S(X)=(s_1,s_2,\ldots,s_{(2d-1)n-d+1})$
of length
![]() $(2d-1)n-d+1$
. To this end, we will reveal the vertices of
$(2d-1)n-d+1$
. To this end, we will reveal the vertices of
![]() $X$
one by one in a specific way. Let
$X$
one by one in a specific way. Let
![]() $v_1$
be the lexicographically smallest vertex of
$v_1$
be the lexicographically smallest vertex of
![]() $X$
, and notice that
$X$
, and notice that
![]() $v_1$
has at most
$v_1$
has at most
![]() $d$
neighbours in
$d$
neighbours in
![]() $X$
. For every
$X$
. For every
![]() $i=1,\ldots,d$
, we let
$i=1,\ldots,d$
, we let
![]() $s_i$
take the value
$s_i$
take the value
![]() $1$
if the
$1$
if the
![]() $i$
th directed edge of the form
$i$
th directed edge of the form
![]() $\vec{u_1v}$
in the above ordering lies in the set of directed edges
$\vec{u_1v}$
in the above ordering lies in the set of directed edges
![]() $\overleftrightarrow{E(X)}$
of
$\overleftrightarrow{E(X)}$
of
![]() $X$
, and
$X$
, and
![]() $0$
otherwise. The ordering of these directed edges induces an ordering on the neighbours of
$0$
otherwise. The ordering of these directed edges induces an ordering on the neighbours of
![]() $u_1$
in
$u_1$
in
![]() $P$
. We reveal the neighbours of
$P$
. We reveal the neighbours of
![]() $u_1$
in
$u_1$
in
![]() $X$
one by one according to the latter ordering, and we let
$X$
one by one according to the latter ordering, and we let
![]() $u_{j+1}$
be the
$u_{j+1}$
be the
![]() $j$
th revealed vertex. Now we proceed to the lexicographically smaller neighbour of
$j$
th revealed vertex. Now we proceed to the lexicographically smaller neighbour of
![]() $u_1$
lying in
$u_1$
lying in
![]() $X$
, denoted
$X$
, denoted
![]() $w$
. The valid directed edges starting from
$w$
. The valid directed edges starting from
![]() $w$
are those not ending at
$w$
are those not ending at
![]() $u_1$
, and there are exactly
$u_1$
, and there are exactly
![]() $2d-1$
of them. The ordering of the whole set of directed edges starting from
$2d-1$
of them. The ordering of the whole set of directed edges starting from
![]() $w$
induces an ordering of the set of valid directed edges starting from
$w$
induces an ordering of the set of valid directed edges starting from
![]() $w$
. For every
$w$
. For every
![]() $i=d+1,\ldots,3d-1$
, we let
$i=d+1,\ldots,3d-1$
, we let
![]() $s_i$
take the value
$s_i$
take the value
![]() $1$
if the
$1$
if the
![]() $(i-d)$
th valid directed edge of the form
$(i-d)$
th valid directed edge of the form
![]() $\vec{wv}$
lies in
$\vec{wv}$
lies in
![]() $\overleftrightarrow{E(X)}$
and
$\overleftrightarrow{E(X)}$
and
![]() $v$
has not been revealed so far (the latter is always true in this step but not necessarily in the following steps), and
$v$
has not been revealed so far (the latter is always true in this step but not necessarily in the following steps), and
![]() $0$
otherwise. We reveal the corresponding neighbours of
$0$
otherwise. We reveal the corresponding neighbours of
![]() $w$
in
$w$
in
![]() $X$
one by one, and we label them
$X$
one by one, and we label them
![]() $u_k,u_{k+1}\ldots,$
where
$u_k,u_{k+1}\ldots,$
where
![]() $k$
is the smallest index not previously used. Now we proceed as before up to the point that all vertices of
$k$
is the smallest index not previously used. Now we proceed as before up to the point that all vertices of
![]() $X$
have been revealed, and we set to
$X$
have been revealed, and we set to
![]() $0$
all the remaining entries of
$0$
all the remaining entries of
![]() $S$
that have not already been set to some value. Notice that
$S$
that have not already been set to some value. Notice that
![]() $S$
contains exactly
$S$
contains exactly
![]() $n-1$
$n-1$
![]() $1$
’s, since
$1$
’s, since
![]() $P$
has size
$P$
has size
![]() $n$
.
$n$
.
We will now prove the following result.
Lemma 8.2.
Consider some
![]() $0\leq x \leq 1$
, and let
$0\leq x \leq 1$
, and let
![]() $y=\min \{x,1/2\}$
. Then
$y=\min \{x,1/2\}$
. Then
In particular,
![]() $\dot{a}_{2d-2}({\mathbb{Z}}^d)=1$
.
$\dot{a}_{2d-2}({\mathbb{Z}}^d)=1$
.
Proof. For
![]() $x=1$
we have
$x=1$
we have
![]() $y=1/2$
, and so the claimed upper bound is equal to
$y=1/2$
, and so the claimed upper bound is equal to
which is in turn equal to
![]() $2f(2d-2)$
. Since
$2f(2d-2)$
. Since
![]() $f(r)$
is an increasing function,
$f(r)$
is an increasing function,
The assertion now follows in the case
![]() $x=1$
from the fact that
$x=1$
from the fact that
![]() $\dot{a}_{2d-3}({\mathbb{Z}}^d)\leq f(2d-3)$
. So let us assume that
$\dot{a}_{2d-3}({\mathbb{Z}}^d)\leq f(2d-3)$
. So let us assume that
![]() $x\lt 1$
.
$x\lt 1$
.
Consider some numbers
![]() $n\in \mathbb{N}$
, and
$n\in \mathbb{N}$
, and
![]() $\epsilon \gt 0$
with
$\epsilon \gt 0$
with
![]() $x+\epsilon \lt 1$
. Let
$x+\epsilon \lt 1$
. Let
![]() $X$
be a lattice site animal of size
$X$
be a lattice site animal of size
![]() $n$
in
$n$
in
![]() ${\mathbb{Z}}^d$
containing
${\mathbb{Z}}^d$
containing
![]() $o$
such that
$o$
such that
![]() $(2d-2-x-\epsilon )n\leq |\partial _V X|\leq (2d-2-x+\epsilon )n$
. Recall Eden’s procedure and the notation introduced there. This procedure defines naturally a spanning subtree
$(2d-2-x-\epsilon )n\leq |\partial _V X|\leq (2d-2-x+\epsilon )n$
. Recall Eden’s procedure and the notation introduced there. This procedure defines naturally a spanning subtree
![]() $T$
of
$T$
of
![]() $X$
rooted at
$X$
rooted at
![]() $u_1$
, by attaching an edge
$u_1$
, by attaching an edge
![]() $u_k u_l$
,
$u_k u_l$
,
![]() $k\lt l$
to
$k\lt l$
to
![]() $T$
when
$T$
when
![]() $u_l$
is one of the neighbours of
$u_l$
is one of the neighbours of
![]() $u_k$
revealed when considering the valid directed edges starting from
$u_k$
revealed when considering the valid directed edges starting from
![]() $u_k$
. Given an edge
$u_k$
. Given an edge
![]() $uv$
of
$uv$
of
![]() $T$
with
$T$
with
![]() $u$
being the ancestor of
$u$
being the ancestor of
![]() $v$
, we say that
$v$
, we say that
![]() $uv$
is a turn of
$uv$
is a turn of
![]() $T$
if
$T$
if
![]() $uv$
is perpendicular to the edge
$uv$
is perpendicular to the edge
![]() $zu$
of
$zu$
of
![]() $T$
, where
$T$
, where
![]() $z$
is the (unique) ancestor of
$z$
is the (unique) ancestor of
![]() $u$
. We denote by
$u$
. We denote by
![]() $t$
the number of turns of
$t$
the number of turns of
![]() $T$
.
$T$
.
Claim 1. We claim that
Indeed, for every
![]() $k=1,2,\ldots,n$
, let
$k=1,2,\ldots,n$
, let
![]() $T_k$
be the subtree of
$T_k$
be the subtree of
![]() $T$
with
$T$
with
![]() $V(T_k)=\{u_1,u_2,\ldots,u_k\}$
. Let
$V(T_k)=\{u_1,u_2,\ldots,u_k\}$
. Let
![]() $\partial T_k$
be the set of vertices in
$\partial T_k$
be the set of vertices in
![]() ${\mathbb{Z}}^d\setminus \{u_1,u_2,\ldots,u_k\}$
having a neighbour in
${\mathbb{Z}}^d\setminus \{u_1,u_2,\ldots,u_k\}$
having a neighbour in
![]() $\{u_1,u_2,\ldots,u_k\}$
. Write
$\{u_1,u_2,\ldots,u_k\}$
. Write
![]() $t_k$
for the number of turns of
$t_k$
for the number of turns of
![]() $T_k$
. We will prove inductively that
$T_k$
. We will prove inductively that
for every
![]() $k=1,2,\ldots,n$
. The claim will then follow once we observe that
$k=1,2,\ldots,n$
. The claim will then follow once we observe that
![]() $|\partial _V X|= |\partial T_n|$
,
$|\partial _V X|= |\partial T_n|$
,
![]() $|X|=|T_n|=n$
and
$|X|=|T_n|=n$
and
![]() $t=t_n$
. For
$t=t_n$
. For
![]() $k=1$
, the assertion clearly holds. Assume that it holds for some
$k=1$
, the assertion clearly holds. Assume that it holds for some
![]() $1\leq k\lt n$
. Notice that we always have
$1\leq k\lt n$
. Notice that we always have
![]() $|T_{k+1}|=|T_k|+1$
and
$|T_{k+1}|=|T_k|+1$
and
![]() $|\partial T_{k+1}|\leq |\partial T_k|+2d-2$
, because
$|\partial T_{k+1}|\leq |\partial T_k|+2d-2$
, because
![]() $u_{k+1}$
lies in
$u_{k+1}$
lies in
![]() $\partial T_k$
and at most
$\partial T_k$
and at most
![]() $2d-1$
neighbours of
$2d-1$
neighbours of
![]() $u_{k+1}$
lie in
$u_{k+1}$
lie in
![]() $\partial T_{k+1}$
. If
$\partial T_{k+1}$
. If
![]() $t_{k+1}=t_k$
, then we get
$t_{k+1}=t_k$
, then we get
![]() $|\partial T_{k+1}|\leq (2d-2)|T_{k+1}|-t_{k+1}+2$
, as claimed. Suppose that
$|\partial T_{k+1}|\leq (2d-2)|T_{k+1}|-t_{k+1}+2$
, as claimed. Suppose that
![]() $t_{k+1}=t_k +1$
. Consider the ancestor
$t_{k+1}=t_k +1$
. Consider the ancestor
![]() $u_l$
of
$u_l$
of
![]() $u_{k+1}$
, and the ancestor
$u_{k+1}$
, and the ancestor
![]() $u_m$
of
$u_m$
of
![]() $u_l$
. Since by adding
$u_l$
. Since by adding
![]() $u_{k+1}$
to
$u_{k+1}$
to
![]() $T_k$
we create one more turn,
$T_k$
we create one more turn,
![]() $u_{k+1}$
,
$u_{k+1}$
,
![]() $u_l$
and
$u_l$
and
![]() $u_m$
are three vertices of a common square. Let
$u_m$
are three vertices of a common square. Let
![]() $w$
be the fourth vertex. Notice that
$w$
be the fourth vertex. Notice that
![]() $w$
lies in
$w$
lies in
![]() $T_k \cup \partial T_k$
. Thus, at most
$T_k \cup \partial T_k$
. Thus, at most
![]() $2d-2$
neighbours of
$2d-2$
neighbours of
![]() $u_{k+1}$
lie in
$u_{k+1}$
lie in
![]() $\partial T_{k+1} \setminus \partial T_k$
. Therefore,
$\partial T_{k+1} \setminus \partial T_k$
. Therefore,
![]() $|\partial T_{k+1}|\leq (2d-2)|T_{k+1}|-t_{k+1}+2$
, as desired. This completes the proof of (19).
$|\partial T_{k+1}|\leq (2d-2)|T_{k+1}|-t_{k+1}+2$
, as desired. This completes the proof of (19).
We will now utilise (19) to prove the statement of the lemma. Our assumption
![]() $(2d-2-x-\epsilon )n\leq |\partial _V X|$
combined with (19) implies that
$(2d-2-x-\epsilon )n\leq |\partial _V X|$
combined with (19) implies that
![]() $t\leq (x+\epsilon )n+2$
. Hence it suffices to find an upper bound for the number of lattice site animals
$t\leq (x+\epsilon )n+2$
. Hence it suffices to find an upper bound for the number of lattice site animals
![]() $Q$
of size
$Q$
of size
![]() $n$
with
$n$
with
![]() $t\leq q\,:\!=(x+\epsilon )n+2$
.
$t\leq q\,:\!=(x+\epsilon )n+2$
.
Claim 2. We claim that the number
![]() $\dot{a}_n$
of such lattice site animals of size
$\dot{a}_n$
of such lattice site animals of size
![]() $n$
satisfies
$n$
satisfies
 \begin{align} \dot{a}_n\leq \sum _{i=1}^d \sum _{j=0}^{\min \{q,n-i\}}\begin{pmatrix}d \\ i\end{pmatrix}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}. \end{align}
\begin{align} \dot{a}_n\leq \sum _{i=1}^d \sum _{j=0}^{\min \{q,n-i\}}\begin{pmatrix}d \\ i\end{pmatrix}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}. \end{align}
Indeed, let
![]() $i$
be number of neighbours of
$i$
be number of neighbours of
![]() $u_1$
in
$u_1$
in
![]() $Q$
, let
$Q$
, let
![]() $j$
be the number of
$j$
be the number of
![]() $1$
’s contributing to the number of turns in those bits of
$1$
’s contributing to the number of turns in those bits of
![]() $S(Q)$
. Let us apply the following steps in turn:
$S(Q)$
. Let us apply the following steps in turn:
-
(i) Set
 $i$
entries of
$i$
entries of
 $(s_1,\ldots,s_d)$
equal to
$(s_1,\ldots,s_d)$
equal to
 $1$
,
$1$
, -
(ii) Choose which entries of
 $S(Q)$
contribute to the number of turns,
$S(Q)$
contribute to the number of turns, -
(iii) Choose which bits, except for the first one, contain an additional
 $1$
.
$1$
.
After the first two steps, we have specified which entries of
![]() $S(Q)$
are set to
$S(Q)$
are set to
![]() $1$
, except for those that do not contribute to the number of turns. Since for every vertex of
$1$
, except for those that do not contribute to the number of turns. Since for every vertex of
![]() $Q$
, at most one of its children does not contribute to the number of turns, we conclude that at most one entry of each of the bits chosen in the fourth step can be set to
$Q$
, at most one of its children does not contribute to the number of turns, we conclude that at most one entry of each of the bits chosen in the fourth step can be set to
![]() $1$
, the position of which in
$1$
, the position of which in
![]() $S(Q)$
is uniquely determined by the values of the remaining entries of
$S(Q)$
is uniquely determined by the values of the remaining entries of
![]() $S(Q)$
. It is easy to see now that for every
$S(Q)$
. It is easy to see now that for every
![]() $i$
and
$i$
and
![]() $j$
, there are at most
$j$
, there are at most
 \begin{equation*}\begin{pmatrix}d \\ i\end{pmatrix}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix} \begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\end{equation*}
\begin{equation*}\begin{pmatrix}d \\ i\end{pmatrix}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix} \begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\end{equation*}
possibilities for
![]() $Q$
, and so (20) can be obtained by summing over all possible values of
$Q$
, and so (20) can be obtained by summing over all possible values of
![]() $i$
and
$i$
and
![]() $j$
.
$j$
.
We will now handle the sum in the right-hand side of (20). Since the binomial coefficient
![]() $(\begin{smallmatrix}m \\ l\end{smallmatrix})$
is an increasing function of
$(\begin{smallmatrix}m \\ l\end{smallmatrix})$
is an increasing function of
![]() $l$
when
$l$
when
![]() $l\leq m/2$
, we have
$l\leq m/2$
, we have
 \begin{equation*}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix}\leq \begin{pmatrix}(2d-1)(n-1) \\ q\end{pmatrix}.\end{equation*}
\begin{equation*}\begin{pmatrix}(2d-1)(n-1) \\ j\end{pmatrix}\leq \begin{pmatrix}(2d-1)(n-1) \\ q\end{pmatrix}.\end{equation*}
Using Stirling’s approximation
![]() $m!=\big (1+o(1)\big ) \sqrt{2\pi m}(m/e)^m$
we obtain
$m!=\big (1+o(1)\big ) \sqrt{2\pi m}(m/e)^m$
we obtain
 \begin{equation*}\begin{pmatrix}(2d-1)(n-1) \\ q\end{pmatrix}\approx \dfrac {(2d-1)^{(2d-1)n}}{(x+\epsilon )^{x+\epsilon }(2d-1-x-\epsilon )^{(2d-1-x-\epsilon )n}},\end{equation*}
\begin{equation*}\begin{pmatrix}(2d-1)(n-1) \\ q\end{pmatrix}\approx \dfrac {(2d-1)^{(2d-1)n}}{(x+\epsilon )^{x+\epsilon }(2d-1-x-\epsilon )^{(2d-1-x-\epsilon )n}},\end{equation*}
where
![]() $\approx$
denotes equality up to a multiplicative constant that is
$\approx$
denotes equality up to a multiplicative constant that is
![]() $O(c^n)$
for every
$O(c^n)$
for every
![]() $c\gt 1$
. Clearly
$c\gt 1$
. Clearly
 \begin{equation*}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\leq 2^n.\end{equation*}
\begin{equation*}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\leq 2^n.\end{equation*}
It follows that
where
![]() $\lesssim$
denotes inequality up to a multiplicative constant that is
$\lesssim$
denotes inequality up to a multiplicative constant that is
![]() $O(c^n)$
for every
$O(c^n)$
for every
![]() $c\gt 1$
. Taking
$c\gt 1$
. Taking
![]() $n$
th roots and letting
$n$
th roots and letting
![]() $n\to \infty$
and
$n\to \infty$
and
![]() $\epsilon \to 0$
we obtain
$\epsilon \to 0$
we obtain
The above bound can be improved when
![]() $x\lt 1/2$
. Suppose that
$x\lt 1/2$
. Suppose that
![]() $x\lt 1/2$
. We can choose
$x\lt 1/2$
. We can choose
![]() $\epsilon \gt 0$
small enough, and increase the value of
$\epsilon \gt 0$
small enough, and increase the value of
![]() $n$
, if necessary, to ensure that
$n$
, if necessary, to ensure that
![]() $q+d\lt n/2$
. Since the binomial coefficient
$q+d\lt n/2$
. Since the binomial coefficient
![]() $(\begin{smallmatrix}m \\ l\end{smallmatrix})$
is a decreasing function of
$(\begin{smallmatrix}m \\ l\end{smallmatrix})$
is a decreasing function of
![]() $l$
when
$l$
when
![]() $l\geq m/2$
, for every
$l\geq m/2$
, for every
![]() $i$
and
$i$
and
![]() $j$
, we have
$j$
, we have
 \begin{equation*}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\leq \begin{pmatrix}n-1 \\ n-d-q\end{pmatrix},\end{equation*}
\begin{equation*}\begin{pmatrix}n-1 \\ n-i-j\end{pmatrix}\leq \begin{pmatrix}n-1 \\ n-d-q\end{pmatrix},\end{equation*}
because
![]() $n-i-j\geq n-d-q \geq n/2$
. Using again Stirling’s approximation, we deduce that
$n-i-j\geq n-d-q \geq n/2$
. Using again Stirling’s approximation, we deduce that
 \begin{equation*}\begin{pmatrix}n-1 \\ n-d-q\end{pmatrix}\approx \big ((x+\epsilon )^{x+\epsilon }(1-x-\epsilon )^{1-x-\epsilon }\big )^{-n}.\end{equation*}
\begin{equation*}\begin{pmatrix}n-1 \\ n-d-q\end{pmatrix}\approx \big ((x+\epsilon )^{x+\epsilon }(1-x-\epsilon )^{1-x-\epsilon }\big )^{-n}.\end{equation*}
We can now conclude that
Taking
![]() $n$
th roots and letting
$n$
th roots and letting
![]() $n\to \infty$
and
$n\to \infty$
and
![]() $\epsilon \to 0$
we obtain
$\epsilon \to 0$
we obtain
Since a site interface is also a lattice site animal and
![]() $\partial P\subset \partial _V P$
, we obtain the following result.
$\partial P\subset \partial _V P$
, we obtain the following result.
Corollary 8.3.
Consider some
![]() $0\leq x \leq 1$
, and let
$0\leq x \leq 1$
, and let
![]() $y=\min \{x,1/2\}$
. Then
$y=\min \{x,1/2\}$
. Then
In particular,
![]() $\dot{b}_{2d-2}({\mathbb{Z}}^d)=1$
.
$\dot{b}_{2d-2}({\mathbb{Z}}^d)=1$
.
We are now ready to prove Theorem 8.1.
Proof of Theorem 8.1
. For every
![]() $0\leq x\leq 1$
, we let
$0\leq x\leq 1$
, we let
where
![]() $y=\min \{x,1/2\}$
. It is not hard to see that there is a constant
$y=\min \{x,1/2\}$
. It is not hard to see that there is a constant
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $x^{-x}\leq C$
for every
$x^{-x}\leq C$
for every
![]() $x\in [0,1]$
, and
$x\in [0,1]$
, and
for every
![]() $y\in [0,1/2]$
. Moreover, for every
$y\in [0,1/2]$
. Moreover, for every
![]() $x\in [0,1]$
we have
$x\in [0,1]$
we have
by the monotonicity of
![]() $2d-1-x$
as a function of
$2d-1-x$
as a function of
![]() $x$
, and
$x$
, and
Thus,
Since
![]() $\dfrac{2d-1}{(2d-2)^{1-x}}$
is an increasing function of
$\dfrac{2d-1}{(2d-2)^{1-x}}$
is an increasing function of
![]() $x$
, it follows by Lemma 8.2 that for every
$x$
, it follows by Lemma 8.2 that for every
we have
Using the standard inequality
![]() $e^{C^2}\geq 1+ C^2$
we obtain
$e^{C^2}\geq 1+ C^2$
we obtain
![]() $e^{-C^2}\leq 1/(1+C^2)$
, hence
$e^{-C^2}\leq 1/(1+C^2)$
, hence
Plugging
![]() $r=2d-2-z$
in (13) we obtain
$r=2d-2-z$
in (13) we obtain
![]() $f(2d-2-z)=2de-5e/2+O(1/\log (d))$
, and so
$f(2d-2-z)=2de-5e/2+O(1/\log (d))$
, and so
for every
![]() $d$
large enough. On the other hand, for every
$d$
large enough. On the other hand, for every
![]() $r\leq 2d-2-z$
we have
$r\leq 2d-2-z$
we have
![]() $\dot{a}_r({\mathbb{Z}}^d)\leq f(2d-2-z)$
by (18), hence
$\dot{a}_r({\mathbb{Z}}^d)\leq f(2d-2-z)$
by (18), hence
by (4.3) for every
![]() $d$
large enough (recall that lattice site animals coincide with site interfaces for a special choice of a basis of the cycle space), which proves our claim.
$d$
large enough (recall that lattice site animals coincide with site interfaces for a special choice of a basis of the cycle space), which proves our claim.
Combining Theorem 8.1 with (10) yields the following lower bound for
![]() ${\dot{p}_c}({\mathbb{Z}}^d)$
.
${\dot{p}_c}({\mathbb{Z}}^d)$
.
Theorem 8.4.
![]() ${\dot{p}_c}({\mathbb{Z}}^d)\geq \dfrac{1}{2d}+\dfrac{2}{(2d)^2}-O(1/d^2\log (d))$
.
${\dot{p}_c}({\mathbb{Z}}^d)\geq \dfrac{1}{2d}+\dfrac{2}{(2d)^2}-O(1/d^2\log (d))$
.
Proof. It follows from (21) that
![]() $b_r\lt f(2d-2-z)\leq f(r)$
for every
$b_r\lt f(2d-2-z)\leq f(r)$
for every
![]() $r\geq 2d-2-z$
, where
$r\geq 2d-2-z$
, where
![]() $z=1-\dfrac{C^2}{\log\! \big (2d-2\big )}$
and
$z=1-\dfrac{C^2}{\log\! \big (2d-2\big )}$
and
![]() $C$
is the constant in the proof of Theorem 8.1. Since
$C$
is the constant in the proof of Theorem 8.1. Since
![]() $b_{\dot{r}_d}({\mathbb{Z}}^d)=f(\dot{r}_d)$
, we obtain
$b_{\dot{r}_d}({\mathbb{Z}}^d)=f(\dot{r}_d)$
, we obtain
Hence,
It is not hard to see
 \begin{align*} \dfrac{1}{2d-2+C^2/\log (2d-2)}&=\dfrac{1}{2d}+\dfrac{2-C^2/\log (2d-2)}{2d\big (2d-2+C^2/\log (2d-2)\big )}\\ & = \dfrac{1}{2d}+\dfrac{2}{(2d)^2}-O(1/d^2\log (d)), \end{align*}
\begin{align*} \dfrac{1}{2d-2+C^2/\log (2d-2)}&=\dfrac{1}{2d}+\dfrac{2-C^2/\log (2d-2)}{2d\big (2d-2+C^2/\log (2d-2)\big )}\\ & = \dfrac{1}{2d}+\dfrac{2}{(2d)^2}-O(1/d^2\log (d)), \end{align*}
which proves the assertion.
We remark that the well-known inequality
![]() ${\dot{p}_c}({\mathbb{Z}}^d)\geq p_c({\mathbb{Z}}^d)$
[Reference Grimmett18] and the asymptotic expansion
${\dot{p}_c}({\mathbb{Z}}^d)\geq p_c({\mathbb{Z}}^d)$
[Reference Grimmett18] and the asymptotic expansion
![]() $p_c({\mathbb{Z}}^d)=\frac{1}{2d}+\frac{1}{(2d)^2}+O(1/d^3)$
, mentioned in the previous section, give a weaker lower bound on
$p_c({\mathbb{Z}}^d)=\frac{1}{2d}+\frac{1}{(2d)^2}+O(1/d^3)$
, mentioned in the previous section, give a weaker lower bound on
![]() ${\dot{p}_c}({\mathbb{Z}}^d)$
.
${\dot{p}_c}({\mathbb{Z}}^d)$
.
Remark: In both Theorem 8.4 and (11) we made implicit use of (6), but it would have sufficed to use its variant for site lattice animals instead of interfaces. Thus adapting Delyon’s [Reference Delyon11] result to site animals would have sufficed.
9. An analogue of the Cheeger constant for interfaces
In this section, we define a variant
![]() $I(G)$
of the Cheeger constant with the aim of using it to obtain new bounds for
$I(G)$
of the Cheeger constant with the aim of using it to obtain new bounds for
![]() $p_c$
.
$p_c$
.
Before introducing the variant
![]() $I(G)$
, let us first recall the definition of the Cheeger constant, which has both an edge and a vertex variant. Given a graph
$I(G)$
, let us first recall the definition of the Cheeger constant, which has both an edge and a vertex variant. Given a graph
![]() $G$
and a finite set of vertices
$G$
and a finite set of vertices
![]() $S$
, we define the edge boundary
$S$
, we define the edge boundary
![]() $\partial _E S$
of
$\partial _E S$
of
![]() $S$
to be the set of edges of
$S$
to be the set of edges of
![]() $G$
with one end vertex in
$G$
with one end vertex in
![]() $S$
and one not in
$S$
and one not in
![]() $S$
. The vertex boundary
$S$
. The vertex boundary
![]() $\partial _V S$
of
$\partial _V S$
of
![]() $S$
is defined to be the set of vertices in
$S$
is defined to be the set of vertices in
![]() $V\setminus S$
that have a neighbour in
$V\setminus S$
that have a neighbour in
![]() $S$
. The edge Cheeger constant of
$S$
. The edge Cheeger constant of
![]() $G$
is defined as
$G$
is defined as
![]() $h_E(G)=\inf _S \frac{|\partial _E S|}{|S|}$
, where the infimum is taken over all finite sets
$h_E(G)=\inf _S \frac{|\partial _E S|}{|S|}$
, where the infimum is taken over all finite sets
![]() $S$
of vertices. The vertex Cheeger constant of
$S$
of vertices. The vertex Cheeger constant of
![]() $G$
is defined as
$G$
is defined as
![]() $h_V(G)=\inf _S \frac{|\partial _V S|}{|S|}$
, where the infimum is taken again over all finite sets of vertices
$h_V(G)=\inf _S \frac{|\partial _V S|}{|S|}$
, where the infimum is taken again over all finite sets of vertices
![]() $S$
. In [Reference Benjamini and Schramm8] Benjamini & Schramm proved that for all non-amenable graphs
$S$
. In [Reference Benjamini and Schramm8] Benjamini & Schramm proved that for all non-amenable graphs
![]() $G$
,
$G$
,
![]() $p_c(G)\leq \frac{1}{h_E(G)+1}$
and
$p_c(G)\leq \frac{1}{h_E(G)+1}$
and
![]() ${\dot{p}_c}(G)\leq \frac{1}{h_V(G)+1}$
.
${\dot{p}_c}(G)\leq \frac{1}{h_V(G)+1}$
.
Analogously to the Cheeger constant, we define the following quantities.
Definition 9.1. We define
where the infimum ranges over all interfaces
![]() $P$
and site interfaces
$P$
and site interfaces
![]() $Q$
, respectively.
$Q$
, respectively.
It is possible that
![]() $I_E(G)\gt 0$
and
$I_E(G)\gt 0$
and
![]() $I_V(G)\gt 0$
while
$I_V(G)\gt 0$
while
![]() $h_E(G)=0$
and
$h_E(G)=0$
and
![]() $h_V(G)=0$
. Examples of such graphs are all Cayley graphs of
$h_V(G)=0$
. Examples of such graphs are all Cayley graphs of
![]() $1$
-ended amenable finitely presented groups. Indeed, it was proved that the cycle space of such graphs admits a basis consisting of cycles of bounded length [Reference Timár42], in which case
$1$
-ended amenable finitely presented groups. Indeed, it was proved that the cycle space of such graphs admits a basis consisting of cycles of bounded length [Reference Timár42], in which case
![]() $I_E(G)\gt 0$
and
$I_E(G)\gt 0$
and
![]() $I_V(G)\gt 0$
by [Reference Georgakopoulos and Panagiotis17, Lemma 10.9].
$I_V(G)\gt 0$
by [Reference Georgakopoulos and Panagiotis17, Lemma 10.9].
In the following theorem, we prove an upper bound on
![]() $p_c$
which is reminiscent of the result of Benjamini & Schramm. Our result applies to graphs for which
$p_c$
which is reminiscent of the result of Benjamini & Schramm. Our result applies to graphs for which
This assumption is satisfied, for example, by the class of graphs
![]() $\mathcal{S}$
that we were working in the previous section for
$\mathcal{S}$
that we were working in the previous section for
![]() $g(n)=n^{\frac{d-1}{d}}$
. It has the following implication. Consider a vertex
$g(n)=n^{\frac{d-1}{d}}$
. It has the following implication. Consider a vertex
![]() $o$
of
$o$
of
![]() $G$
and let
$G$
and let
![]() $X$
be an infinite geodesic starting from
$X$
be an infinite geodesic starting from
![]() $o$
. Let
$o$
. Let
![]() $P$
be a site interface of
$P$
be a site interface of
![]() $o$
such that
$o$
such that
![]() $|\partial P|=n$
. Then
$|\partial P|=n$
. Then
Theorem 9.2.
Let
![]() $G$
be an
$G$
be an
![]() $1$
-ended,
$1$
-ended,
![]() $2$
-connected graph
$2$
-connected graph
![]() $G$
satisfying (22). Then we have
$G$
satisfying (22). Then we have
Proof. We will prove the assertion for bond percolation. The case of site percolation is similar.
If
![]() $I_E(G)=0$
there is nothing to prove, so let us assume that
$I_E(G)=0$
there is nothing to prove, so let us assume that
![]() $I_E(G)\gt 0$
. Let
$I_E(G)\gt 0$
. Let
![]() $q=\frac{1}{I_E(G)+1}$
and
$q=\frac{1}{I_E(G)+1}$
and
![]() $r=1/{I_E(G)}$
. We claim that for every
$r=1/{I_E(G)}$
. We claim that for every
![]() $p\gt q$
the expected number of occurring multi-interfaces of boundary size
$p\gt q$
the expected number of occurring multi-interfaces of boundary size
![]() $n$
decays exponentially in
$n$
decays exponentially in
![]() $n$
. Indeed, let
$n$
. Indeed, let
![]() $\mathcal{P}_{n}$
be the (random) number of occurring multi-interfaces
$\mathcal{P}_{n}$
be the (random) number of occurring multi-interfaces
![]() $P$
with
$P$
with
![]() $|\partial P|=n$
. Notice that
$|\partial P|=n$
. Notice that
hence
![]() $\mathcal{P}_{n}\leq G(n)$
, where
$\mathcal{P}_{n}\leq G(n)$
, where
![]() $G(n)=e^{o(n)}$
, because at most
$G(n)=e^{o(n)}$
, because at most
![]() $g(k)$
interfaces of size smaller that
$g(k)$
interfaces of size smaller that
![]() $k$
can occur in any percolation configuration
$k$
can occur in any percolation configuration
![]() $\omega$
. Indeed, we can choose
$\omega$
. Indeed, we can choose
![]() $G(n)=p(rn)\max \{g(n_1)\ldots g(n_i)\}$
, where the maximum ranges over all possible partitions of
$G(n)=p(rn)\max \{g(n_1)\ldots g(n_i)\}$
, where the maximum ranges over all possible partitions of
![]() $rn$
. It is not hard to see that
$rn$
. It is not hard to see that
![]() $G(n)=e^{o(n)}$
.
$G(n)=e^{o(n)}$
.
Now for any
![]() $p\gt q$
and every
$p\gt q$
and every
![]() $m\leq rn$
we have
$m\leq rn$
we have
 \begin{gather*} p^m (1-p)^n=q^m (1-q)^n (p/q)^m \Big (\dfrac{1-p}{1-q}\Big )^n \leq \\ q^m (1-q)^n (p/q)^{rn} \Big (\dfrac{1-p}{1-q}\Big )^n =q^m (1-q)^n \big (f(r)\big )^n p^{rn} (1-p)^n, \end{gather*}
\begin{gather*} p^m (1-p)^n=q^m (1-q)^n (p/q)^m \Big (\dfrac{1-p}{1-q}\Big )^n \leq \\ q^m (1-q)^n (p/q)^{rn} \Big (\dfrac{1-p}{1-q}\Big )^n =q^m (1-q)^n \big (f(r)\big )^n p^{rn} (1-p)^n, \end{gather*}
which implies that
Notice that
![]() $f(r) p^r (1-p)\lt 1$
, which proves our claim.
$f(r) p^r (1-p)\lt 1$
, which proves our claim.
The fact that
![]() $\mathbb E_p(\mathcal{P}_n)$
decays exponentially in
$\mathbb E_p(\mathcal{P}_n)$
decays exponentially in
![]() $n$
implies that the sum
$n$
implies that the sum
 \begin{equation*}\sum _{n=1}^\infty \sum _{\substack {P\in \mathcal {MI} \\ |\partial P|=n}} (-\!1)^{c(P)+1} {\mathbb {P}}_p(\text {$P$ occurs})\end{equation*}
\begin{equation*}\sum _{n=1}^\infty \sum _{\substack {P\in \mathcal {MI} \\ |\partial P|=n}} (-\!1)^{c(P)+1} {\mathbb {P}}_p(\text {$P$ occurs})\end{equation*}
converges absolutely, where
![]() $\mathcal{MI}$
is the set of multi-interfaces, and
$\mathcal{MI}$
is the set of multi-interfaces, and
![]() $c(P)$
is the number of component interfaces of
$c(P)$
is the number of component interfaces of
![]() $P$
. The inclusion-exclusion principle then implies that we can express
$P$
. The inclusion-exclusion principle then implies that we can express
![]() $1-\theta$
as
$1-\theta$
as
 \begin{equation*}1-\theta (p)=\sum _{n=1}^\infty \sum _{\substack {P\in \mathcal {MS} \\ |\partial P|=n}} (\!-\!1)^{c(P)+1} {\mathbb {P}}_p(P\ \text {occurs})\end{equation*}
\begin{equation*}1-\theta (p)=\sum _{n=1}^\infty \sum _{\substack {P\in \mathcal {MS} \\ |\partial P|=n}} (\!-\!1)^{c(P)+1} {\mathbb {P}}_p(P\ \text {occurs})\end{equation*}
for every
![]() $p\gt \frac{1}{I_E(G)+1}$
. We claim that the latter sum is an analytic function on
$p\gt \frac{1}{I_E(G)+1}$
. We claim that the latter sum is an analytic function on
![]() $\Big(\frac{1}{I_E(G)+1},1\Big]$
. To prove this, we will use [Reference Georgakopoulos and Panagiotis17, Corollary 4.14], which states that any such expression is analytically provided the following two conditions are satisfied. Firstly, the event
$\Big(\frac{1}{I_E(G)+1},1\Big]$
. To prove this, we will use [Reference Georgakopoulos and Panagiotis17, Corollary 4.14], which states that any such expression is analytically provided the following two conditions are satisfied. Firstly, the event
![]() $\{P\ \text{occurs}\}$
should depend on
$\{P\ \text{occurs}\}$
should depend on
![]() $\Theta (|\partial P|)$
edges for every
$\Theta (|\partial P|)$
edges for every
![]() $P\in \mathcal{MS}$
, and secondly, for every
$P\in \mathcal{MS}$
, and secondly, for every
![]() $q\in \Big(\frac{1}{I_E(G)+1},1\Big)$
, there exists
$q\in \Big(\frac{1}{I_E(G)+1},1\Big)$
, there exists
![]() $0\lt c=c(q)\lt 1$
such that
$0\lt c=c(q)\lt 1$
such that
 \begin{equation*}\sum _{\substack {P\in \mathcal {MS} \\ |\partial P|=n}} (-\!1)^{c(P)+1} {\mathbb {P}}_p(\text {$P$ occurs})=O(c^n)\end{equation*}
\begin{equation*}\sum _{\substack {P\in \mathcal {MS} \\ |\partial P|=n}} (-\!1)^{c(P)+1} {\mathbb {P}}_p(\text {$P$ occurs})=O(c^n)\end{equation*}
for every
![]() $p\in (q,1)$
. In our case, the first condition follows from (24). The second condition follows from (25) and the fact that for every
$p\in (q,1)$
. In our case, the first condition follows from (24). The second condition follows from (25) and the fact that for every
![]() $q\in \Big(\frac{1}{I_E(G)+1},1\Big)$
, there exists
$q\in \Big(\frac{1}{I_E(G)+1},1\Big)$
, there exists
![]() $0\lt c=c(q)\lt 1$
such that
$0\lt c=c(q)\lt 1$
such that
![]() $f(r) p^r (1-p)\leq c$
for every
$f(r) p^r (1-p)\leq c$
for every
![]() $p\in (q,1)$
. We can thus deduce that
$p\in (q,1)$
. We can thus deduce that
![]() $\theta$
is analytic on the interval
$\theta$
is analytic on the interval
![]() $\Big(\frac{1}{I_E(G)+1},1\Big]$
. Since
$\Big(\frac{1}{I_E(G)+1},1\Big]$
. Since
![]() $\theta$
is not analytic at
$\theta$
is not analytic at
![]() $p_c$
, it follows that
$p_c$
, it follows that
![]() $p_c(G)\leq \frac{1}{I_E(G)+1}$
.
$p_c(G)\leq \frac{1}{I_E(G)+1}$
.
Remark 9.3. There is an alternative way to prove Theorem 9.2, without showing that
![]() $\theta$
is analytic, by means of (24) and a Peierls-type of argument. However, this alternative way is not simpler. We emphasise that the exponential decay of
$\theta$
is analytic, by means of (24) and a Peierls-type of argument. However, this alternative way is not simpler. We emphasise that the exponential decay of
![]() $\mathbb E_p(\mathcal{P}_n)$
does not imply, in general, that
$\mathbb E_p(\mathcal{P}_n)$
does not imply, in general, that
![]() $p\gt p_c$
, as it can happen that
$p\gt p_c$
, as it can happen that
![]() $\mathbb E_p(\mathcal{P}_n)$
decays exponentially for some
$\mathbb E_p(\mathcal{P}_n)$
decays exponentially for some
![]() $p\lt p_c$
.
$p\lt p_c$
.
Clearly
![]() $I_E(G)\geq h_E(G)$
and
$I_E(G)\geq h_E(G)$
and
![]() $I_V(G)\geq h_V(G)$
, hence the above theorem gives an alternative proof of the result of Benjamini & Schramm mentioned above.
$I_V(G)\geq h_V(G)$
, hence the above theorem gives an alternative proof of the result of Benjamini & Schramm mentioned above.
Question 9.4.
For which (transitive) non-amenable graphs does the strict inequality
![]() $I_E(G)\gt h_E(G)$
(
$I_E(G)\gt h_E(G)$
(
![]() $I_V(G)\gt h_V(G)$
) hold?
$I_V(G)\gt h_V(G)$
) hold?
It has been recently proved that
![]() $I_V(G)\gt h_V(G)$
holds for the
$I_V(G)\gt h_V(G)$
holds for the
![]() $d$
-regular triangulations and quadrangulations of the hyperbolic plane [Reference Haslegrave and Panagiotis23].
$d$
-regular triangulations and quadrangulations of the hyperbolic plane [Reference Haslegrave and Panagiotis23].
10. Strict inequalities
As we already observed, interfaces are a special species of lattice animals. In this section, we will show that there are exponentially fewer interfaces than lattice animals for a large class of graphs. Building on this result, we will then show that the strict inequality
![]() $\dot{p}_c\lt \frac{1}{h_V+1}$
holds for a large class of non-amenable graphs. It will be more convenient for us to work with the site variants of interfaces and lattice animals.
$\dot{p}_c\lt \frac{1}{h_V+1}$
holds for a large class of non-amenable graphs. It will be more convenient for us to work with the site variants of interfaces and lattice animals.
We start by introducing some notation regarding site interfaces on general graphs. Consider an
![]() $1$
-ended,
$1$
-ended,
![]() $2$
-connected, bounded degree graph
$2$
-connected, bounded degree graph
![]() $G$
. Furthermore, assume that both P5 and (22) are satisfied. For example, we can take
$G$
. Furthermore, assume that both P5 and (22) are satisfied. For example, we can take
![]() $G$
to be a Cayley graph of an
$G$
to be a Cayley graph of an
![]() $1$
-ended, finitely presented group. We fix a basis of the cycle space consisting of cycles of bounded length and we consider the family of site interfaces associated with this basis. As we are working with a general graph which might not have any symmetries, the number of site interfaces might depend on the base vertex
$1$
-ended, finitely presented group. We fix a basis of the cycle space consisting of cycles of bounded length and we consider the family of site interfaces associated with this basis. As we are working with a general graph which might not have any symmetries, the number of site interfaces might depend on the base vertex
![]() $o$
. For this reason, given a vertex
$o$
. For this reason, given a vertex
![]() $o$
of
$o$
of
![]() $G$
, we define
$G$
, we define
![]() $\dot{b}_{n,o}=\dot{b}_{n,o}(G)$
to be the number of site interfaces
$\dot{b}_{n,o}=\dot{b}_{n,o}(G)$
to be the number of site interfaces
![]() $P$
of
$P$
of
![]() $o$
with
$o$
with
![]() $|P|=n$
and we let
$|P|=n$
and we let
![]() $\dot{b}_n=\dot{b}_n(G)\,:\!=\sup _{o\in V(G)} \dot{b}_{n,o}$
. We now define
$\dot{b}_n=\dot{b}_n(G)\,:\!=\sup _{o\in V(G)} \dot{b}_{n,o}$
. We now define
![]() $\dot{b}=\dot{b}(G)\,:\!=\limsup _{n\to \infty } \dot{b}^{1/n}_n$
.
$\dot{b}=\dot{b}(G)\,:\!=\limsup _{n\to \infty } \dot{b}^{1/n}_n$
.
As above, given a vertex
![]() $o$
of
$o$
of
![]() $G$
, we define
$G$
, we define
![]() $\dot{a}_{n,o}=\dot{a}_{n,o}(G)$
as the number of lattice site animals containing
$\dot{a}_{n,o}=\dot{a}_{n,o}(G)$
as the number of lattice site animals containing
![]() $o$
with
$o$
with
![]() $n$
vertices and we let
$n$
vertices and we let
![]() $\dot{a}_n=\dot{a}_n(G)\,:\!=\sup _{o\in V(G)} \dot{a}_{n,o}$
. We now define
$\dot{a}_n=\dot{a}_n(G)\,:\!=\sup _{o\in V(G)} \dot{a}_{n,o}$
. We now define
![]() $\dot{a}=\dot{a}(G)\,:\!=\limsup _{n\to \infty } \dot{a}^{1/n}_n$
.
$\dot{a}=\dot{a}(G)\,:\!=\limsup _{n\to \infty } \dot{a}^{1/n}_n$
.
For every vertex
![]() $v$
of
$v$
of
![]() $G$
, we let
$G$
, we let
![]() $\mathcal{P}_v$
be the set of basic cycles containing
$\mathcal{P}_v$
be the set of basic cycles containing
![]() $v$
and we let
$v$
and we let
![]() $C_v$
be the union of all cycles in
$C_v$
be the union of all cycles in
![]() $\mathcal{P}_v$
. Using an argument similar to that in the proof of Kesten’s pattern theorem for self-avoiding walks [Reference Kesten28], we will prove that the following holds.
$\mathcal{P}_v$
. Using an argument similar to that in the proof of Kesten’s pattern theorem for self-avoiding walks [Reference Kesten28], we will prove that the following holds.
Theorem 10.1.
Let
![]() $G$
be an
$G$
be an
![]() $1$
-ended,
$1$
-ended,
![]() $2$
-connected, bounded degree graph
$2$
-connected, bounded degree graph
![]() $G$
satisfying
P5
and (22). Then
$G$
satisfying
P5
and (22). Then
![]() $\dot{b}(G)\lt \dot{a}(G)$
.
$\dot{b}(G)\lt \dot{a}(G)$
.
Proof. Consider a site interface
![]() $P$
of
$P$
of
![]() $o$
of size
$o$
of size
![]() $n$
. We will introduce a local operation that turns
$n$
. We will introduce a local operation that turns
![]() $P$
into a lattice site animal that is not a site interface. To this end, let
$P$
into a lattice site animal that is not a site interface. To this end, let
![]() $l$
be the length of the longest cycle in
$l$
be the length of the longest cycle in
![]() $\mathcal{P}$
. Consider a set of vertices
$\mathcal{P}$
. Consider a set of vertices
![]() $S$
of
$S$
of
![]() $P$
with the property that any two vertices in
$P$
with the property that any two vertices in
![]() $S$
are at distance at least
$S$
are at distance at least
![]() $2l+1$
apart, and
$2l+1$
apart, and
![]() $S$
is a maximal set with respect to this property. It is not hard to see that the graphs
$S$
is a maximal set with respect to this property. It is not hard to see that the graphs
![]() $C_v$
,
$C_v$
,
![]() $v\in S$
are pairwise disjoint. Moreover, we have
$v\in S$
are pairwise disjoint. Moreover, we have
![]() $|S|\geq n/d^{4l+2}$
, where
$|S|\geq n/d^{4l+2}$
, where
![]() $d$
is the maximal degree of
$d$
is the maximal degree of
![]() $G$
, because the maximality of
$G$
, because the maximality of
![]() $S$
implies that any vertex of
$S$
implies that any vertex of
![]() $P$
is at distance at most
$P$
is at distance at most
![]() $4l+2$
from some vertex in
$4l+2$
from some vertex in
![]() $S$
.
$S$
.
Let
![]() $0\lt \varepsilon \lt 1/d^{4l+2}$
. For each subset
$0\lt \varepsilon \lt 1/d^{4l+2}$
. For each subset
![]() $T$
of
$T$
of
![]() $S$
of cardinality
$S$
of cardinality
![]() $m=\left \lfloor{\varepsilon n}\right \rfloor$
, we let
$m=\left \lfloor{\varepsilon n}\right \rfloor$
, we let
![]() $P(T)=(\cup _{v\in T}C_v)\cup P$
. Recall that by (iv), a vertex
$P(T)=(\cup _{v\in T}C_v)\cup P$
. Recall that by (iv), a vertex
![]() $v$
is included in
$v$
is included in
![]() $P$
only if there is a
$P$
only if there is a
![]() $\mathcal{P}$
-path in
$\mathcal{P}$
-path in
![]() $G\setminus \partial P$
connecting
$G\setminus \partial P$
connecting
![]() $v$
to
$v$
to
![]() $\vec{\partial P^{D}}$
, hence
$\vec{\partial P^{D}}$
, hence
![]() $C_v$
is not contained entirely in
$C_v$
is not contained entirely in
![]() $P$
. It follows that among the vertices in
$P$
. It follows that among the vertices in
![]() $S$
, only those in
$S$
, only those in
![]() $T$
have the property that
$T$
have the property that
![]() $C_v$
is contained in
$C_v$
is contained in
![]() $P(T)$
. Thus the graphs
$P(T)$
. Thus the graphs
![]() $P(T)$
are pairwise distinct and there are
$P(T)$
are pairwise distinct and there are
![]() $(\begin{smallmatrix}|S| \\ m\end{smallmatrix})$
of them.
$(\begin{smallmatrix}|S| \\ m\end{smallmatrix})$
of them.
Our aim now is to find a lower bound for the cardinality of the set
To this end, we need to count the number of pre-images of each
![]() $P(T)$
. Let
$P(T)$
. Let
![]() $P^{\prime}$
be a site interface of size
$P^{\prime}$
be a site interface of size
![]() $n$
and
$n$
and
![]() $T^{\prime}$
be a set of vertices of
$T^{\prime}$
be a set of vertices of
![]() $P^{\prime}$
such that
$P^{\prime}$
such that
![]() $P^{\prime}(T^{\prime})=P(T)$
. Notice that any vertex of
$P^{\prime}(T^{\prime})=P(T)$
. Notice that any vertex of
![]() $T^{\prime}$
needs to be at distance at most
$T^{\prime}$
needs to be at distance at most
![]() $2l$
from some vertex in
$2l$
from some vertex in
![]() $T$
. Hence
$T$
. Hence
![]() $P^{\prime}$
coincides with
$P^{\prime}$
coincides with
![]() $P$
on vertices at distance at most
$P$
on vertices at distance at most
![]() $3l$
from some vertex in
$3l$
from some vertex in
![]() $T$
. Thus there are at most
$T$
. Thus there are at most
![]() $2^{d^{3l}m}$
possibilities for
$2^{d^{3l}m}$
possibilities for
![]() $P^{\prime}$
and
$P^{\prime}$
and
![]() $T^{\prime}$
.
$T^{\prime}$
.
Overall, we obtain
 \begin{equation*}|Y_n|\geq \dfrac {\bigg(\begin{array}{l}m \\ k\end{array}\bigg)}{2^{d^{3l}m}}\dot {b}_{n,o},\end{equation*}
\begin{equation*}|Y_n|\geq \dfrac {\bigg(\begin{array}{l}m \\ k\end{array}\bigg)}{2^{d^{3l}m}}\dot {b}_{n,o},\end{equation*}
where
![]() $r=\left \lceil{n/d^{4l+2}}\right \rceil$
. Using Stirling’s approximation
$r=\left \lceil{n/d^{4l+2}}\right \rceil$
. Using Stirling’s approximation
![]() $N!=N^Ne^{-N+o(N)}$
, we obtain
$N!=N^Ne^{-N+o(N)}$
, we obtain
We can now deduce that
where
![]() $C=2^{d^{3l}}d^{4l+2}$
. Choosing
$C=2^{d^{3l}}d^{4l+2}$
. Choosing
![]() $\varepsilon =\big (C(2\dot{b})^{d^l}\big )^{-1}$
we obtain that
$\varepsilon =\big (C(2\dot{b})^{d^l}\big )^{-1}$
we obtain that
We claim that
for some
![]() $n\leq k \leq n+d^l m$
and some vertex
$n\leq k \leq n+d^l m$
and some vertex
![]() $v$
. Indeed, the size of each element of
$v$
. Indeed, the size of each element of
![]() $Y_n$
varies between
$Y_n$
varies between
![]() $n$
and
$n$
and
![]() $n+d^l m$
, so for some
$n+d^l m$
, so for some
![]() $n\leq k \leq n+d^l m$
, the number of elements of
$n\leq k \leq n+d^l m$
, the number of elements of
![]() $Y_n$
of size
$Y_n$
of size
![]() $k$
is at least
$k$
is at least
![]() $(2\dot{b})^{d^l \varepsilon n+o(n)}\dot{b}_{n,o}$
. Now (23) implies that for some vertex
$(2\dot{b})^{d^l \varepsilon n+o(n)}\dot{b}_{n,o}$
. Now (23) implies that for some vertex
![]() $v$
, the number of elements of
$v$
, the number of elements of
![]() $Y_n$
of size
$Y_n$
of size
![]() $k$
that contain
$k$
that contain
![]() $v$
is at least
$v$
is at least
![]() $(2\dot{b})^{d^l \varepsilon n+o(n)}\dot{b}_{n,o}$
, which proves the claim.
$(2\dot{b})^{d^l \varepsilon n+o(n)}\dot{b}_{n,o}$
, which proves the claim.
Choosing some
![]() $o$
that maximises
$o$
that maximises
![]() $\dot{b}_{n,o}$
, we obtain that
$\dot{b}_{n,o}$
, we obtain that
for some
![]() $n\leq k \leq n+d^l m$
and some vertex
$n\leq k \leq n+d^l m$
and some vertex
![]() $v=v(n)$
. Taking the
$v=v(n)$
. Taking the
![]() $k$
th root and letting
$k$
th root and letting
![]() $k$
tend to infinity, we obtain that
$k$
tend to infinity, we obtain that
because
![]() $k\leq n+d^l m\leq (1+d^l \varepsilon )n$
. This proves the desired result.
$k\leq n+d^l m\leq (1+d^l \varepsilon )n$
. This proves the desired result.
We will now assume that
![]() $G$
is a non-amenable graph. As already mentioned, it is a well-known result of Benjamin & Schramm that
$G$
is a non-amenable graph. As already mentioned, it is a well-known result of Benjamin & Schramm that
![]() $\dot{p}_c(G)\leq 1/(h_V+1)$
[Reference Benjamini and Schramm8]. We prove that this inequality is in fact strict.
$\dot{p}_c(G)\leq 1/(h_V+1)$
[Reference Benjamini and Schramm8]. We prove that this inequality is in fact strict.
Theorem 10.2.
Let
![]() $G$
be an
$G$
be an
![]() $1$
-ended,
$1$
-ended,
![]() $2$
-connected, bounded degree, non-amenable graph
$2$
-connected, bounded degree, non-amenable graph
![]() $G$
satisfying
P5
. Then
$G$
satisfying
P5
. Then
![]() $\dot{p}_c(G)\lt \frac{1}{h_V(G)+1}$
.
$\dot{p}_c(G)\lt \frac{1}{h_V(G)+1}$
.
Proof. We will prove that for the values of
![]() $p$
in a neighbourhood of
$p$
in a neighbourhood of
![]() $1/(h_V(G)+1)$
, the expected number of occurring site interfaces of size
$1/(h_V(G)+1)$
, the expected number of occurring site interfaces of size
![]() $n$
decays exponentially in
$n$
decays exponentially in
![]() $n$
. This easily implies the theorem as for example, we can argue as in the proof of Theorem 9.2 to deduce that
$n$
. This easily implies the theorem as for example, we can argue as in the proof of Theorem 9.2 to deduce that
![]() $\theta$
is analytic in a neighbourhood of
$\theta$
is analytic in a neighbourhood of
![]() $1/(h_V(G)+1)$
.
$1/(h_V(G)+1)$
.
Consider some
![]() $\delta \in (0,1/h_V)$
and let
$\delta \in (0,1/h_V)$
and let
![]() $I_{n,\delta }$
be the set of site interfaces
$I_{n,\delta }$
be the set of site interfaces
![]() $P$
such that
$P$
such that
![]() $|\partial P|=n$
and
$|\partial P|=n$
and
![]() $|P|\geq (1/h_V-\delta ) n$
. We will show that for a small enough
$|P|\geq (1/h_V-\delta ) n$
. We will show that for a small enough
![]() $\delta$
, the expected number of occurring elements of
$\delta$
, the expected number of occurring elements of
![]() $I_{n,\delta }$
decays exponentially. Arguing as in the proof of Theorem 10.1 and using the notation introduced there, we can associate to
$I_{n,\delta }$
decays exponentially. Arguing as in the proof of Theorem 10.1 and using the notation introduced there, we can associate to
![]() $I_{n,\delta }$
a set
$I_{n,\delta }$
a set
![]() $Y_{n,\delta }$
of connected subgraphs such that
$Y_{n,\delta }$
of connected subgraphs such that
Given
![]() $P\in I_{n,\delta }$
,
$P\in I_{n,\delta }$
,
![]() $Q\in Y_{n,\delta }$
with
$Q\in Y_{n,\delta }$
with
![]() $P$
being a pre-image of
$P$
being a pre-image of
![]() $Q$
, we would like to show that
$Q$
, we would like to show that
![]() ${\mathbb{P}}_p(P \text{ occurs})$
is not much larger than
${\mathbb{P}}_p(P \text{ occurs})$
is not much larger than
![]() ${\mathbb{P}}_p(Q \text{ is open and } \partial _V Q \text{ is closed})$
(the latter is the probability that
${\mathbb{P}}_p(Q \text{ is open and } \partial _V Q \text{ is closed})$
(the latter is the probability that
![]() $Q$
is a cluster). In order to do this, we need to estimate the size of
$Q$
is a cluster). In order to do this, we need to estimate the size of
![]() $\partial _V Q$
. To this end, let
$\partial _V Q$
. To this end, let
![]() $D$
be the union of all the finite components of
$D$
be the union of all the finite components of
![]() $G\setminus \partial P$
. By (ii) and (iv),
$G\setminus \partial P$
. By (ii) and (iv),
![]() $P$
is contained in
$P$
is contained in
![]() $D$
and
$D$
and
![]() $\partial _V D=\partial P$
. Notice that
$\partial _V D=\partial P$
. Notice that
which implies that
Since
![]() $Q$
can be obtained from
$Q$
can be obtained from
![]() $P$
by adding at most
$P$
by adding at most
![]() $d^l$
vertices at
$d^l$
vertices at
![]() $\left \lfloor{\varepsilon |P|}\right \rfloor$
places, we obtain that
$\left \lfloor{\varepsilon |P|}\right \rfloor$
places, we obtain that
![]() $|Q| \leq (1+d^l \varepsilon )|P|$
. Moreover, by considering the size of the neighbourhood of
$|Q| \leq (1+d^l \varepsilon )|P|$
. Moreover, by considering the size of the neighbourhood of
![]() $Q\setminus P$
, we see that
$Q\setminus P$
, we see that
where the term
![]() $|D|-|P|$
comes from the fact that
$|D|-|P|$
comes from the fact that
![]() $\partial _V P\setminus \partial P\subset D\setminus P$
. Using (26) and the last inequality, we find that
$\partial _V P\setminus \partial P\subset D\setminus P$
. Using (26) and the last inequality, we find that
for a certain constant
![]() $K\gt 0$
. We can now choose
$K\gt 0$
. We can now choose
![]() $\delta =\varepsilon$
small enough that for every
$\delta =\varepsilon$
small enough that for every
![]() $p\in [h_V/2,(h_V+1)/2]$
we have
$p\in [h_V/2,(h_V+1)/2]$
we have
Now the non-amenability of
![]() $G$
implies that each
$G$
implies that each
![]() $Q\in Y_{n,\delta }$
contains one of the first
$Q\in Y_{n,\delta }$
contains one of the first
![]() $2^{o(n)}$
vertices of
$2^{o(n)}$
vertices of
![]() $X$
, hence
$X$
, hence
![]() $\sum _{Q\in Y_{n,\delta }}{\mathbb{P}}_p(Q \text{ is open and } \partial _V Q \text{ is closed})=2^{o(n)}$
which in turn implies that
$\sum _{Q\in Y_{n,\delta }}{\mathbb{P}}_p(Q \text{ is open and } \partial _V Q \text{ is closed})=2^{o(n)}$
which in turn implies that
![]() $\sum _{P\in I_{n,\delta }}{\mathbb{P}}_p(P \text{ occurs})$
decays exponentially in
$\sum _{P\in I_{n,\delta }}{\mathbb{P}}_p(P \text{ occurs})$
decays exponentially in
![]() $n$
.
$n$
.
On the other hand, it follows from Lemma 4.7 that for every
![]() $x\gt 0$
, the expected number of occurring interfaces
$x\gt 0$
, the expected number of occurring interfaces
![]() $P$
with
$P$
with
![]() $|\partial P| =n$
and
$|\partial P| =n$
and
![]() $|P|\lt \big (\frac{p}{1-p}-x\big )n$
decays exponentially in
$|P|\lt \big (\frac{p}{1-p}-x\big )n$
decays exponentially in
![]() $n$
. Hence for every
$n$
. Hence for every
![]() $p\gt q\,:\!= \frac{1-h\delta }{h+1-h\delta }$
, the expected number of occurring interfaces
$p\gt q\,:\!= \frac{1-h\delta }{h+1-h\delta }$
, the expected number of occurring interfaces
![]() $P$
with
$P$
with
![]() $|\partial P| =n$
and
$|\partial P| =n$
and
under
![]() ${\mathbb{P}}_p$
, decays exponentially in
${\mathbb{P}}_p$
, decays exponentially in
![]() $n$
, because
$n$
, because
![]() $\frac{q}{1-q}\lt \frac{p}{1-p}$
. Since we have
$\frac{q}{1-q}\lt \frac{p}{1-p}$
. Since we have
![]() $q\lt 1/(h+1)$
, the latter exponential decay holds at a neighbourhood of
$q\lt 1/(h+1)$
, the latter exponential decay holds at a neighbourhood of
![]() $1/(h+1)$
. This completes the proof.
$1/(h+1)$
. This completes the proof.
11. Conclusion
In this paper, we obtained basic properties of the function
![]() $b_r(G)$
, and connected it to percolation theory and the enumeration of lattice animals. Many questions about
$b_r(G)$
, and connected it to percolation theory and the enumeration of lattice animals. Many questions about
![]() $b_r(G)$
are left open, of which we mention just a few. We remarked that
$b_r(G)$
are left open, of which we mention just a few. We remarked that
![]() $\max _r b_r(G)$
is interesting, as it coincides with
$\max _r b_r(G)$
is interesting, as it coincides with
![]() $b(G)$
, which lower bounds the growth rate
$b(G)$
, which lower bounds the growth rate
![]() $a(G)$
of lattice animals. We expect that this maximum is attained at a single point
$a(G)$
of lattice animals. We expect that this maximum is attained at a single point
![]() $r= r_{max}$
. What can be said about
$r= r_{max}$
. What can be said about
![]() $r_{max}$
? Is it always greater than
$r_{max}$
? Is it always greater than
![]() $r(p_c)$
? Is their ratio, or some other expression, independent of the lattice
$r(p_c)$
? Is their ratio, or some other expression, independent of the lattice
![]() $G$
once the dimension is fixed?
$G$
once the dimension is fixed?
We observed that
![]() $b_r$
is a continuous, almost everywhere differentiable function of
$b_r$
is a continuous, almost everywhere differentiable function of
![]() $r$
. Are stronger smoothness conditions satisfied? Is it smooth/analytic at every
$r$
. Are stronger smoothness conditions satisfied? Is it smooth/analytic at every
![]() $r\neq r(p_c), r(1-p_c)$
?
$r\neq r(p_c), r(1-p_c)$
?
Appendix A: Continuity of the decay exponents
In this appendix, we prove that the rate of exponential decay
of the cluster size distribution – which is known to exist for every
![]() $p\in (0,1)$
[Reference Bandyopadhyay, Steif and Timár3, Reference Grimmett18] – is a continuous function of
$p\in (0,1)$
[Reference Bandyopadhyay, Steif and Timár3, Reference Grimmett18] – is a continuous function of
![]() $p$
. This applies to bond and site percolation on our class of graphs
$p$
. This applies to bond and site percolation on our class of graphs
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
The fact that
![]() $c(p)\lt 1$
for
$c(p)\lt 1$
for
![]() $p\lt p_c$
is a celebrated result of Aizenman & Barsky [Reference Aizenman and Barsky1]. For
$p\lt p_c$
is a celebrated result of Aizenman & Barsky [Reference Aizenman and Barsky1]. For
![]() $p=p_c$
, we always have
$p=p_c$
, we always have
![]() $c(p)=1$
. For
$c(p)=1$
. For
![]() $p\gt p_c$
various behaviours can arise depending on the underlying lattice [Reference Aizenman, Delyon and Souillard2, Reference Hermon and Hutchcroft24, Reference Kesten and Zhang29]. Our continuity result applies to the whole interval
$p\gt p_c$
various behaviours can arise depending on the underlying lattice [Reference Aizenman, Delyon and Souillard2, Reference Hermon and Hutchcroft24, Reference Kesten and Zhang29]. Our continuity result applies to the whole interval
![]() $p\in (0,1)$
.
$p\in (0,1)$
.
We will also prove the analogous continuity result for the (upper) exponential growth rate of
![]() $\mathbb E_p(N_n)$
, that is
$\mathbb E_p(N_n)$
, that is
![]() $\limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
, whereas before
$\limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
, whereas before
![]() $N_n$
denotes the number of occurring (site) interfaces.
$N_n$
denotes the number of occurring (site) interfaces.
We will start by proving the continuity of
![]() $c(p)$
.
$c(p)$
.
Theorem 12.1.
Consider bond or site percolation on a graph in
![]() $\mathcal{S}$
. Then
$\mathcal{S}$
. Then
![]() $c(p)$
is a continuous function of
$c(p)$
is a continuous function of
![]() $p\in (0,1)$
.
$p\in (0,1)$
.
Proof. Let
![]() $I$
be a compact subinterval of
$I$
be a compact subinterval of
![]() $(0,1)$
. Define
$(0,1)$
. Define
![]() $g_n(p)\,:\!={\mathbb{P}}_p(|C_o|=n)^{1/n}$
, and notice that
$g_n(p)\,:\!={\mathbb{P}}_p(|C_o|=n)^{1/n}$
, and notice that
![]() $0\leq g_n(p)\leq 1$
. Moreover,
$0\leq g_n(p)\leq 1$
. Moreover,
![]() $g_n$
is a differentiable function with derivative equal to
$g_n$
is a differentiable function with derivative equal to
![]() $g_n(p) \dfrac{{\mathbb{P}}_p ^{\prime}(|C_o|=n)}{n{\mathbb{P}}_p(|C_o|=n)}$
, where
$g_n(p) \dfrac{{\mathbb{P}}_p ^{\prime}(|C_o|=n)}{n{\mathbb{P}}_p(|C_o|=n)}$
, where
![]() ${\mathbb{P}}_p ^{\prime}(|C_o|=n)$
denotes the derivative of
${\mathbb{P}}_p ^{\prime}(|C_o|=n)$
denotes the derivative of
![]() ${\mathbb{P}}_p(|C_o|=n)$
. Expressing
${\mathbb{P}}_p(|C_o|=n)$
. Expressing
![]() ${\mathbb{P}}_p ^{\prime}(|C_o|=n)$
via
${\mathbb{P}}_p ^{\prime}(|C_o|=n)$
via
where the sum ranges over all lattice (site) animals of size
![]() $n$
, we conclude that there is a constant
$n$
, we conclude that there is a constant
![]() $c=c(I)\gt 0$
such that
$c=c(I)\gt 0$
such that
![]() $|{\mathbb{P}}_p ^{\prime}(|C_o|=n)|\leq cn{\mathbb{P}}_p (|C_o|=n)$
for every
$|{\mathbb{P}}_p ^{\prime}(|C_o|=n)|\leq cn{\mathbb{P}}_p (|C_o|=n)$
for every
![]() $p\in I$
. Therefore,
$p\in I$
. Therefore,
![]() $g_n ^{\prime}$
is uniformly bounded on
$g_n ^{\prime}$
is uniformly bounded on
![]() $I$
, hence
$I$
, hence
![]() $g_n$
is a
$g_n$
is a
![]() $c$
- Lipschitz function on
$c$
- Lipschitz function on
![]() $I$
. The pointwise convergence of
$I$
. The pointwise convergence of
![]() $g_n$
to
$g_n$
to
![]() $c(p)$
implies that
$c(p)$
implies that
![]() $c(p)$
is a
$c(p)$
is a
![]() $c$
-Lipschitz function on
$c$
-Lipschitz function on
![]() $I$
, hence a continuous function.
$I$
, hence a continuous function.
Define
![]() $B_p\,:\!=\limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
. Before proving the continuity of
$B_p\,:\!=\limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
. Before proving the continuity of
![]() $B_p$
, we will show that
$B_p$
, we will show that
![]() $\lim _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
exists for every
$\lim _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
exists for every
![]() $p$
.
$p$
.
Proposition 12.2.
Consider bond or site percolation on a graph in
![]() $\mathcal{S}$
. Then for every
$\mathcal{S}$
. Then for every
![]() $p\in (0,1)$
, the limit
$p\in (0,1)$
, the limit
![]() $\lim _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
exists.
$\lim _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
exists.
Proof. For simplicity, we will prove the assertion for interfaces in
![]() ${\mathbb{Z}}^d$
and
${\mathbb{Z}}^d$
and
![]() $\mathbb{T}^d$
. Let
$\mathbb{T}^d$
. Let
![]() $m$
and
$m$
and
![]() $n$
be positive integers. We will consider interfaces without any restriction on the surface-to-volume ratio. Arguing as in the proof of Proposition 6.1 we combine
$n$
be positive integers. We will consider interfaces without any restriction on the surface-to-volume ratio. Arguing as in the proof of Proposition 6.1 we combine
![]() $m$
interfaces
$m$
interfaces
![]() $P_1,P_2,\ldots,P_m$
of size
$P_1,P_2,\ldots,P_m$
of size
![]() $n$
that have the same shape, and attach a horizontal path to
$n$
that have the same shape, and attach a horizontal path to
![]() $P_m$
, to obtain an interface of size
$P_m$
, to obtain an interface of size
![]() $k=m(n+4)+s$
for some
$k=m(n+4)+s$
for some
![]() $s$
between
$s$
between
![]() $0$
and
$0$
and
![]() $n+3$
. Notice that the number of attached edges that were initially lying in some
$n+3$
. Notice that the number of attached edges that were initially lying in some
![]() $\partial P_i$
is equal to
$\partial P_i$
is equal to
![]() $2m-1$
. The probability that the resulting interface occurs is equal to
$2m-1$
. The probability that the resulting interface occurs is equal to
![]() $p^k(1-p)^{M-(2m-1)+N}$
, where
$p^k(1-p)^{M-(2m-1)+N}$
, where
![]() $M=\sum _{i=1}^m|\partial P_i|$
, and
$M=\sum _{i=1}^m|\partial P_i|$
, and
![]() $N$
is the number of remaining boundary edges of the interface. It is not hard to see that
$N$
is the number of remaining boundary edges of the interface. It is not hard to see that
![]() $N\leq Cm$
for some constant
$N\leq Cm$
for some constant
![]() $C\gt 0$
. Hence
$C\gt 0$
. Hence
Summing over all possible sequences
![]() $(P_1,P_2,\ldots,P_m)$
we obtain
$(P_1,P_2,\ldots,P_m)$
we obtain
Taking the
![]() $k$
th root, and then letting
$k$
th root, and then letting
![]() $m\to \infty$
and
$m\to \infty$
and
![]() $n\to \infty$
, we obtain that
$n\to \infty$
, we obtain that
![]() $\liminf _{n\to \infty } \mathbb E_p(N_n)^{1/n}\geq \limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
, which implies the desired assertion.
$\liminf _{n\to \infty } \mathbb E_p(N_n)^{1/n}\geq \limsup _{n\to \infty } \mathbb E_p(N_n)^{1/n}$
, which implies the desired assertion.
The proof of Theorem 12.1 applies mutatis mutandis to
![]() $B_p$
: instead of defining
$B_p$
: instead of defining
![]() $g_n(p)$
as
$g_n(p)$
as
![]() ${\mathbb{P}}_p(|C_o|=n)^{1/n}$
, we define
${\mathbb{P}}_p(|C_o|=n)^{1/n}$
, we define
![]() $g_n(p)\,:\!=\mathbb E_p(N_n)^{1/n}$
, and we use the fact that
$g_n(p)\,:\!=\mathbb E_p(N_n)^{1/n}$
, and we use the fact that
![]() $\mathbb E_p(N_n)\leq ln+1$
.
$\mathbb E_p(N_n)\leq ln+1$
.
Corollary 12.3.
Consider bond or site percolation on a graph in
![]() $\mathcal{S}$
. Then
$\mathcal{S}$
. Then
![]() $B_p$
is a continuous function of
$B_p$
is a continuous function of
![]() $p\in (0,1)$
.
$p\in (0,1)$
.