Article contents
A note on distinct distances
Published online by Cambridge University Press: 16 July 2020
Abstract
We show that, for a constant-degree algebraic curve γ in ℝD, every set of n points on γ spans at least Ω(n4/3) distinct distances, unless γ is an algebraic helix, in the sense of Charalambides [2]. This improves the earlier bound Ω(n5/4) of Charalambides [2].
We also show that, for every set P of n points that lie on a d-dimensional constant-degree algebraic variety V in ℝD, there exists a subset S ⊂ P of size at least Ω(n4/(9+12(d−1))), such that S spans 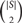 $\left({\begin{array}{*{20}{c}} {|S|} \\ 2 \\\end{array}} \right)$ distinct distances. This improves the earlier bound of Ω(n1/(3d)) of Conlon, Fox, Gasarch, Harris, Ulrich and Zbarsky [4].
$\left({\begin{array}{*{20}{c}} {|S|} \\ 2 \\\end{array}} \right)$ distinct distances. This improves the earlier bound of Ω(n1/(3d)) of Conlon, Fox, Gasarch, Harris, Ulrich and Zbarsky [4].
Both results are consequences of a common technical tool.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
Work on this paper was supported by Grant 892/13 from the Israel Science Foundation, by the Israeli Centers of Research Excellence (I-CORE) program (Center No. 4/11), and by a Shulamit Aloni Fellowship from the Israeli Ministry of Science.
References
- 4
- Cited by


